Построение PWM для последовательности Козак H.sapiens
Чтобы построить позиционную весовую матрицу для последовательности Козак человека, были выбраны 100 случайных генов, для которых известны координаты стартовых ATG. Для этого был использован написанный мной скрипт selection.py, который принимает на вход таблицу с информацией о генах человека human-genes.tsv и создает два файла:
- learn_genes.txt содержит выравнивание без гэпов 100 нуклеотидных последовательностей, каждая из которых - 7 нуклеотидов до ATG + ATG + 3 нуклеотида после ATG (обущающая выборка последовательностей Козак). С помощью этой выборки будет строится PWM.
- test_genes.txt содержит выравнивание без гэпов 300 нуклеотидных последовательностей, каждая из которых - 7 нуклеотидов до ATG + ATG + 3 нуклеотида после ATG (тестовая выборка последовательностей Козак)
Далее был написан скрипт negative.py который отобрал 300 последовательностей внутри случайных генов (то есть по сути нет оснований считать что ATG-окресность кодирует начало трансляции) и выдает файл negative_test_genes.txt, содержащий выравнивание без гэпов 300 нуклеотидных последовательностей, каждая из которых - 7 нуклеотидов до ATG + ATG + 3 нуклеотида после ATG (выборка негативного контроля последовательностей Козак).
После этого была создана позиционная весовая матрица и с помощью данной матрицы вычислены веса последовательностей каждой выборки (GC=41% [3], pseudocounts=0.1). Гистограммы распределения весов последовательностей представлены на рисунке 3 (Для осуществления данных действий также был мною написан скрипт pwm_build.py). По данным гистограммам можно
примерно оценить порог веса при котором мы считаем что последовательность содержит последовательность Козак. Пусть пороговое значение будет равно 4-м.
Таблица 1. PWM.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|---|
| A |
-0.293 |
-0.249 |
-0.899 |
-0.34 |
0.279 |
-0.206 |
-0.676 |
1.218 |
-5.691 |
-5.691 |
-0.206 |
-0.089 |
-0.551 |
| C |
0.312 |
0.158 |
0.381 |
0.506 |
-0.312 |
0.617 |
0.95 |
-5.327 |
-5.327 |
-5.327 |
-0.455 |
0.643 |
0.115 |
| G |
0.476 |
0.445 |
0.668 |
0.275 |
0.506 |
0.115 |
0.158 |
-5.327 |
-5.327 |
1.582 |
0.851 |
-0.823 |
0.668 |
| T |
-0.551 |
-0.34 |
-0.494 |
-0.494 |
-0.899 |
-0.676 |
-1.305 |
-5.691 |
1.218 |
-5.691 |
-0.676 |
-0.166 |
-0.389 |
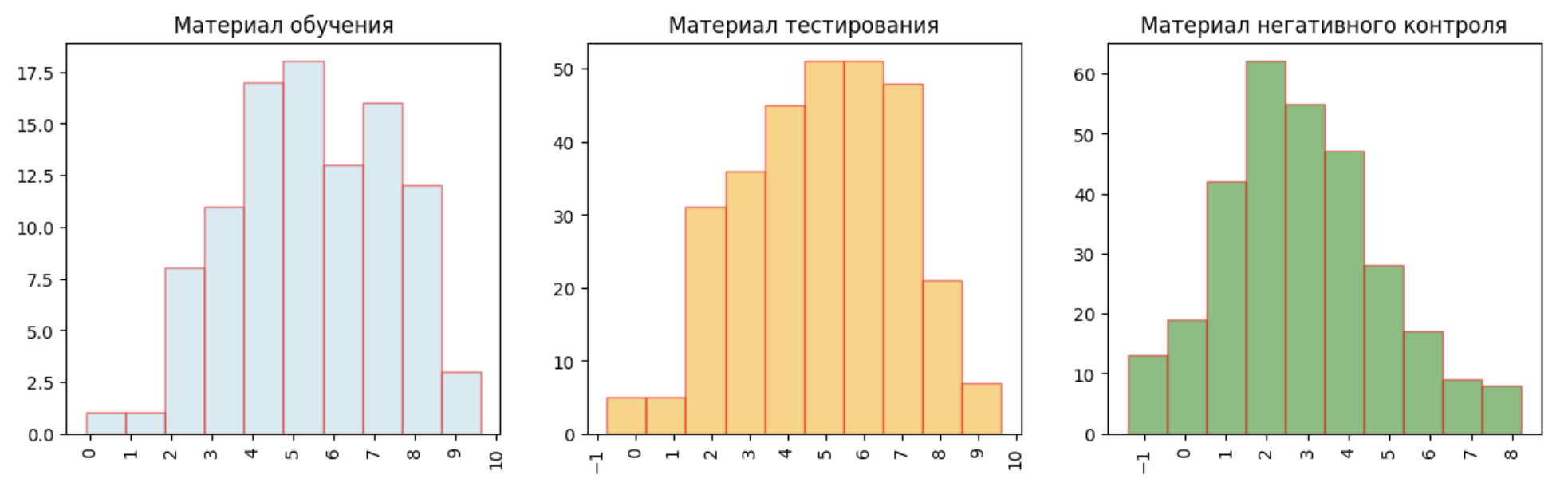Рис. 2. Распределение весов последовательностей. Голубой цвет - обущающая выборка, оранжевый цвет - тестовая выборка, зеленый цвет - выборка негативного контроля.
Далее было определено количество положительных и отрицательных сигналов в каждой из трех выборок по порогу (результат в таблице 2). Несмотря на то, что в обучающей и тестовой выборках нашлись последовательности с отрицательным сигналом, процент положительных сигналов в обущающей выборке и тестовой выборке равен 74% и 67% соответственно, в то время как для выборки негативного контроля данный процент равен 26, что говорит нам о том что данный порог неплохо определяет положительный сигнал.
Таблица 2. Таблица с количеством последовательностей, отобранных по порогу в трех выборках.
|
Обучение |
Положительный контроль |
Отрицательный контроль |
| Cигнал(+) |
74 (74%) |
200 (66.7%) |
79 (26.3%) |
| Cигнал(-) |
26 (26%) |
100 (33.3%) |
221 (73.7%) |
Информационное содержание последовательности Козак H.sapiens
В данном разделе с помощью обучающей выборки и скрипта ic_builder.py была построена матрица информационного содержания последовательности Козак (таблица 3). Также с помощью сервиса
WebLogo3 был построен Logo (рисунок 3). Из схемы видно, что позиции 2,4,5,7-12, имеют значимый информационный вес, т.е.
есть основания считать, что данные выравненные последовательности обладают специфической функцией.
Таблица 3. Матрица информационного содержания IC для последовательности Козак H.sapiens.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|---|
| A |
-0.093 |
-0.083 |
-0.156 |
-0.103 |
0.157 |
-0.071 |
-0.146 |
1.761 |
0.0 |
0.0 |
-0.071 |
-0.034 |
-0.135 |
| C |
0.126 |
0.055 |
0.165 |
0.248 |
-0.068 |
0.338 |
0.726 |
0.0 |
0.0 |
0.0 |
-0.085 |
0.362 |
0.038 |
| G |
0.227 |
0.206 |
0.386 |
0.107 |
0.248 |
0.038 |
0.055 |
0.0 |
0.0 |
2.286 |
0.589 |
-0.107 |
0.386 |
| T |
-0.135 |
-0.103 |
-0.128 |
-0.128 |
-0.156 |
-0.146 |
-0.151 |
0.0 |
1.761 |
0.0 |
-0.146 |
-0.06 |
-0.112 |
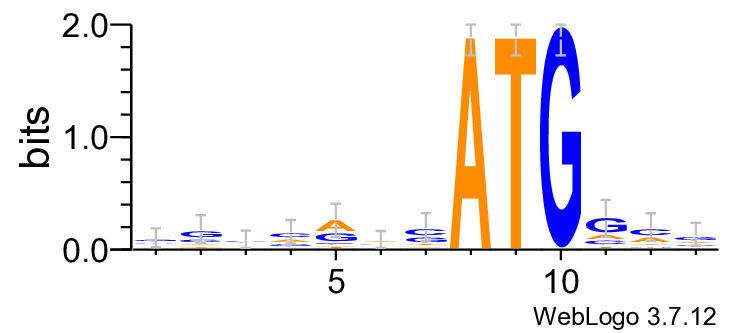Рис. 3. Визуализация информационного содержания последовательности
Подсчет числа сайтов GAATTC в полном геноме одного штамма E.coli
В этом задании я использволала геном штама
E. coli O157:H7 str. Sakai
. Для подсчета количества сайтов GAATTC в геноме был использован
скрипт
.
Всего в геноме оказалось 787 таких сайтов, ожидаемое число GAATTC было подсчитано как произведение частот соответствующих оснований с учётом GC-состава генома, помноженное на длину генома. В итоге ожидаемое число сайтов оказалось равным 1312, что значительно больше полученного. Разница между ожидаемым и полученным значением равна 525.
Для оценки статистической значимости я использовала тест Пуассона со средним 1312, получилось значение p-value = P(x <= 787). Подсчет в WolframAlpha дал результат p-vaslue = 1.69e-55, что означает, что разница между ожидаемым и наблюдаемым значениями встречаемости GAATTC статистически значима. Это объясняется тем, что данный сайт является сайтом рестрикции и его встречаемость находится под отрицательным давлением отбора.
Список литературы
1. Kathryn D. Mouzakis, Andrew L. Lang, Kirk A. Vander Meulen, Preston D. Easterday, Samuel E. Butcher, HIV-1 frameshift efficiency is primarily determined by the stability of base pairs positioned at the mRNA entrance channel of the ribosome, Nucleic Acids Research, Volume 41, Issue 3, 1 February 2013, Pages 1901–1913, https://doi.org/10.1093/nar/gks1254
2. Jacks T, Power MD, Masiarz FR, Luciw PA, Barr PJ, Varmus HE. Characterization of ribosomal frameshifting in HIV-1 gag-pol expression. Nature. 1988 Jan 21;331(6153):280-3. doi: 10.1038/331280a0. PMID: 2447506.
3. International Human Genome Sequencing Consortium. Initial sequencing and analysis of the human genome. Nature 409, 860–921 (2001). https://doi.org/10.1038/35057062