Алгоритмы множественного выравнивания последовательностей

Алгоритм сравнения разных выравниваний одного набора последовательностей

Мной, Всеволодом Маслениковым и Даниилом Нагорным был реализован алгоритм сравнения разных выравниваний одних и тех же последовательностей (подробнее здесь).

Сравнение результатов выравнивания одного набора последовательностей разными алгоритмами множественного выравнивания

Были построены множественные выравнивания последовательностей Ran-ГТФаз (белков, играющих важную роль в транспорте через ядерные поры) при помощи алгоритмов MSAProbs, MAFFT и MUSCLE (в каждом выравнивании 23 последовательности). В качестве референса рассматривался результат выравнивания алгоритмом MSAProbs, показавший наибольшую точность среди рассматриваемых трех алгоритмов в тестах на референсных выравниваниях базы BAliBase [1].

Для сравнения множественных выравниваний использовались упомянутая выше программа сравнения множественных выраниваний MACHO и редактор Jalview (см. S1 и S2). При поиске идентичных колонок учитывались только колонки, содержащие не более, чем 3 гэпа. Длина выравниваний составила 244 колонки для MSAProbs и MAFFT, 245 колонок для MUSCLE. Между выравниваниями MSAProbs и MAFFT имелись 197 идентичных колонок (6 блоков), между MSAProbs и MUSCLE - 183 (4 блока и 1 отдельная колонка).

И выравнивание алгоритмом MAFFT, и выранивание алгоритмом MUSCLE имели 3 крупных блока, идентичных примерно совпадающим участкам выравнивания MSAProbs. На "C-концевом" же участке выравниваний сходство результата MAFFT с результатом MSAProbs было выше, нежели для MUSCLE и MSAProbs (Рис. 1). Сходства и различия между результатами работы алгоритмов множественного выравнивания зависят от особенностей самих алгоритмов. Полученный результат в целом согласуется с тем, что MAFFT по точности ближе к MSAProbs, чем MUSCLE, однако однозначно утверждать о связи между данными фактами нельзя.

MAFFT vs MUSCLE
Рисунок 1. Последние колонки выравниваний алгоритмами MAFFT и MUSCLE. Показаны блоки и колонки, совпадающие с таковыми в выравнивании алгоритмом MSAProbs.

Сравнение выравнивания по совмещению структур с выравниванием алгоритмом MAFFT

Для построения структурного выравнивания было выбрано семейство доменов субъединицы ScpB комплекса расхождения (сегрегации) и конденсации (PF04079). Данный конденсин-подобный комплекс принимает участие в расхождении хромосом при делении бактериальной клетки [2].

Были выбраны белки, содержащие домен, из Mycobacterium tuberculosis (2Z99), Pyrococcus yayanosii (6JUV) и Chlorobium tepidum (1T6S), и для них построено выравнивание на основании совмещения структур (Рис. 2).

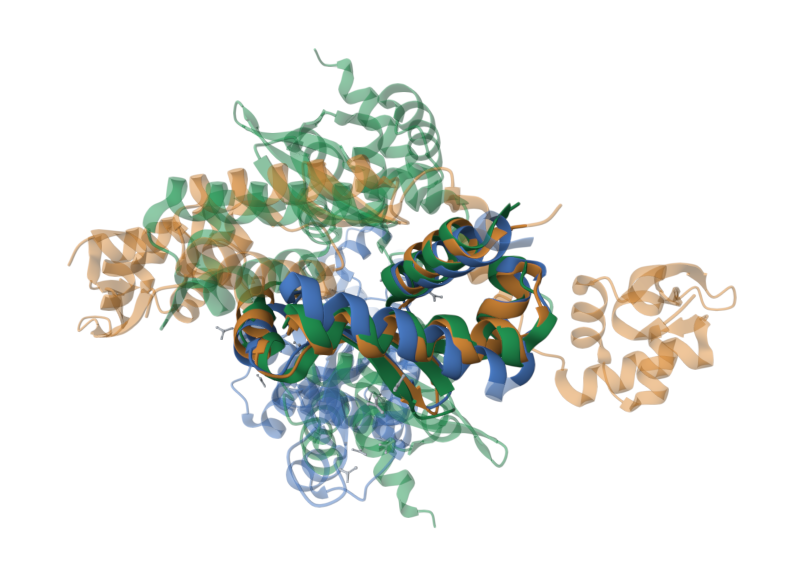
ScpB 3D alignment
Рисунок 2. Совмещение структур трех белков, содержащих домен ScpB.

Также было получено выравнивание данных последовательностей алгоритмом MAFFT и проведен поиск идентичных колонок между полученными выравниваниями (см. S3 и S4). Данные выравнивания в значительной степени различаются, имеются лишь 3 совпадающих блока (доля совпадающих колонок составила 13.16% для структурного выравнивания и 19.07% для выравнивания MAFFT, при сравнении учитывались лишь колонки, не содержащие гэпы). Стоит отметить, что все совпадающие блоки находятся внутри домена из семейства ScpB (координаты 11-162 для Chlorobium tepidum, 19-176 для Mycobacterium tuberculosis и 14-160 для Pyrococcus yayanosii).

Описание алгоритма MAFFT

MAFFT (Multiple Alignment using Fast Fourier Transform) - представленная в 2002 году программа для создания множественных выравниваний нуклеотидных и белковых последовательностей. На момент своего создания MAFFT являлся одной из лучших программ множественного выравнивания по скорости и точности, каким остается и по сей день. Особенностью данного алгоритма является использование быстрого преобразования Фурье (FFT) при попарном выравнивании последовательностей [3].

Работу MAFFT при построении выравнивания можно разделить на следующие этапы:

  1. Попарные выравнивания последовательностей с применением FFT.

  2. Построение направляющего дерева при помощи алгоритма UPGMA.

  3. Прогрессивное выравнивание с учетом весов последовательностей.

  4. Итеративное рафинирование, включающее перестройку направляющего дерева и перестройку выравнивания.

Основной идеей алгоритма является представление последовательности символов в последовательность векторов, где каждый символ (аминокислотный остаток или нуклеотид) преобразуется в вектор, заданный значениями объема и полярности для аминокислот или частотой каждого из четырех нуклеотидов в данной позиции для нуклеотидов. В результате последовательность преобразуется в матрицу (Рис. 3), которую можно рассматривать как многомерный сигнал, что позволяет в дальнейшем применить FFT.

MAFFT vectors
Рисунок 3. Представление аминокислотной последовательности в виде матрицы (последовательности векторов) на основании объема и полярности аминокислотных остатков [4]. Важное уточнение: в реальности алгоритм MAFFT оперирует нормализованными значениями данных параметров, выраженными через среднее значение и стандартное отклонение.

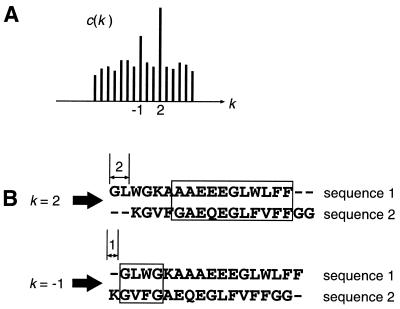
При парном выравнивании последовательностей сначала происходит подсчет корреляции (с) между последовательностями при различных значениях фазового сдвига (k) одной последовательности относительно другой. Прямой подсчет корреляции для каждого значения фазового сдвига для двух последовательностей длиной N имел бы сложность O(N2), однако применение быстрого преобразования Фурье к каждой из последовательностей (которые в данный момент представляют собой многомерные числовые сигналы) и дальнейший подсчет корреляции с использованием результатов преобразования уменьшает сложность процесса до O(NlogN). Далее используется полученная зависимость корреляции от фазового сдвига - c(k).

Зависимость c(k) имеет некоторые пики, соотвествующие значениям сдвига, при которых совмещаются сходные регионы. Для дальнейшего анализа используются 20 наиболее значительных пиков. Для определения координат регионов с высоким сходством для каждого из 20 выбранных значений фазового сдвига происходит их поиск скользящим окном размером в 30 сайтов (Рис. 4). Регионы в которых значение локального сходства превышает заданный порог, считаются гомологичными. Сложность данного этапа не превышает O(N).

MAFFT correlation
Рисунок 4. Зависимость корреляции от фазового сдвига (A), видны 2 пика при значениях k -1 и 2. Поиск участков гомологии скользящим окном для двух значений сдвига (B) скользящим окнов размером в 4 сайта (в данном случае аминокислотных остатка). Если участки идут подряд или прекрываются, они объединяются в один. [3]

Следующим этапом является построение матрицы гомологии, в которой сопоставляются координаты гомологичных сегментов в двух последовательностях (Рис. 5). Далее происходит выбор оптимального "пути" по сегментам с учетом порядка их расположения в последовательностях (Рис. 5A), часть гомологичных сегментов при этом могут исключаться из расчета, после чего общая матрица гомологии делится на неколько подматриц по границам, определенным по центрам выбранных гомологичных сегментов (Рис. 5B). Затем происходит выравнивание последовательностей в полученных подматрицах методами динамического программирования. Поскольку большая часть общей матрицы гомологии исключена из расчета, сложность данного этапа не превышает O(NlogN), тогда как сложность создания выравнивания двух последовательностей методами динамического программирования без применения описанных преобразований составляет O(N2).

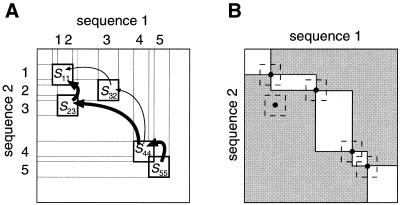
MAFFT matrix
Рисунок 5. Выбор порядка сегментов гомологии с учетом из расположения в последовательностях (A) и разбиение общей матрицы гомологии на подматрицы (B, серая часть матрицы исключается из расчета) по центрам этих сегментов. Стоит отметить, что на рисунке B был выбран путь S55-S44-S32-S11. [3]

Таким образом общая сложность построения выравнивания двух последовательностей составляет O(NlogN), что позволяет значительно сокращать время расчетов по сравнению с обычным глобальным выравниванием двух последовательностей, имеющим сложность O(N2).

На этапе прогрессивного выравнивания (после построения направляющего дерева при помощи UPGMA) построение выравниваний групп уже выровненных последовательностей происходит также, как и выравнивание обычных последовательностей, лишь векторы для каждой позиции перерасчитываются с учетом весов последовательностей в группе.

В процессе итеративного уточнения также используется описанный метод выранивания последовательностей при локальных перестройках итогового выравнивания, что сокращает время этого этапа. Помимо перестройки выравнивания на этапе итеративного рафинирования происходит перестройка направляющего дерева в соответствие с текущим множественным выравниванием.

Благодаря комбинации эффективных методов построения парных выравниваний и итеративного уточнения MAFFT остается одной из лучших программ для создания множественных выравниваний.

СОПРОВОДИТЕЛЬНЫЕ МАТЕРИАЛЫ

  1. Проект Jalview со сравниваемыми множественными выраниваниями Ran-ГТФаз

  2. Таблица с координатами совпадающих блоков и колонок в выравниваниях Ran-ГТФаз

  3. Проект Jalview со сравниваемыми выраниванием по совмещению структур и выравниванием алгоритмом MAFFT

  4. Таблица с координатами совпадающих блоков и колонок в выравнивании по совмещению структур и выравнивании алгоритмом MAFFT

ЛИТЕРАТУРА И ИСТОЧНИКИ

  1. Yongqing Zhang, Qiang Zhang, Jiliu Zhou, Quan Zou, A survey on the algorithm and development of multiple sequence alignment, Briefings in Bioinformatics, Volume 23, Issue 3, May 2022, bbac069, https://doi.org/10.1093/bib/bbac069

  2. Bürmann, F., Shin, HC., Basquin, J. et al. An asymmetric SMC–kleisin bridge in prokaryotic condensin. Nat Struct Mol Biol 20, 371–379 (2013). https://doi.org/10.1038/nsmb.2488

  3. Katoh K, Misawa K, Kuma K, Miyata T. MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002 Jul 15;30(14):3059-66. doi: 10.1093/nar/gkf436. PMID: 12136088; PMCID: PMC135756.

  4. Bogardt, Richard & Jones, Barry & Dwulet, Francis & Garner, William & Lehman, Lee & Gurd, Frank. (1980). Evolution of the amino acid substitution in the mammalian myoglobin gene. Journal of molecular evolution. 15. 197-218. 10.1007/BF01732948.