Выравнивание последовательностей, соответствующих листьям
моего дерева, было переведено из Fasta-формата в формат Phylip
программой ClustalW.
Bootstrap
Программа seqboot (из пакета Phylip) сделала
из выравнивания 100 бутстреп-реплик.
С помощью dnaml по репликам были получены деревья
(в виде скобочных формул).
После анализа (consense) было построено дерево из наиболее
часто встречавшихся ветвей.
Ветви, вошедшие в конечное дерево: Ветвь Сколько раз встретилась (из 100) ABCDEF ..**** 100.00 ...**. 95.00 ..***. 83.00 Ветви, не вошедшие в конечное дерево: Ветвь Сколько раз встретилась (из 100) ABCDEF ...*** 17.00 ...*.* 4.00 ....** 1.00
| Конечное дерево:
+-------------leafC
+-83.0-|
| | +------leafD
+100.0-| +-95.0-|
| | +------leafE
+------| |
| | +--------------------leafF
| |
| +---------------------------leafA
|
+----------------------------------leafB
Дерево неукоренённое! | Реальное дерево для сравнения:
|
Полученное дерево совпало с реальным.
Jackknife
Далее были проведены те же самые манипуляции, но
программа seqboot использовала другой алгоритм — Jackknife.
Полученные результаты:
Ветви, вошедшие в конечное дерево: Ветвь Сколько раз встретилась (из 100) ABCDEF **.... 100.00 ...**. 97.00 ..***. 83.00 Ветви, не вошедшие в конечное дерево: Ветвь Сколько раз встретилась (из 100) ABCDEF ***... 17.00 ***.*. 3.00
| Конечное дерево:
+------leafE
+-97.0-|
+-83.0-| +------leafD
| |
+------| +-------------leafC
| |
| | +------leafB
| +-------100.0-|
| +------leafA
|
+---------------------------leafF
Дерево неукоренённое! | Реальное дерево для сравнения:
|
Полученное дерево также совпало с реальным,
причём в 100 пробных репликах правильные ветви
попадались немного чаще, чем в методе Bootstrap .
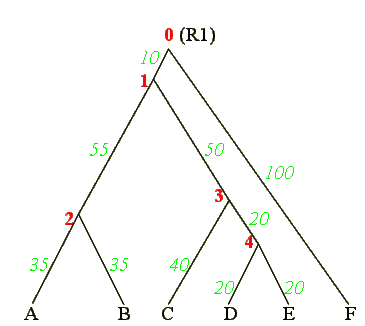
Визуализация деревьев
Программами пакета Phylip проводилась обработка
дерева, полученного ранее программой eneighbor по
методу Neighbor-Joining.
Неукоренённое дерево, нарисованное drawtree:
 |
С помощью retree дерево было укоренено
в среднюю точку, и нарисовано как прямоугольная филограмма
программой drawgram:
 |
Восстановление предковой последовательности
Восстановление ведётся по последовательностям листьев
программой dnaml.
Дерево, полученное по методу Maximum Likelihood:
+-------leafB | | +--------------------------leafF | | 1------------------4 +---leafE | | +---3 | +-------2 +----leafD | | | +---------leafC | +--------leafA
Для выравнивания взята восстановленная последовательность
узла 4 (и соответствующая последовательность узла 1 по нумерации
исходного дерева), поскольку она расположена ближе всего к корню.
Итог: 59,8% совпадений, 73,6% сходства.
| * | 2 | 0 | * | 4 | 0 | * | 6 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | G | c | t | g | a | t | a | a | c | g | a | c | g | a | T | t | t | g | c | G | g | c | a | a | a | t | c | g | c | g | c | a | t | c | t | g | c | g | A | c | g | t | g | a | a | t | a | c | a | c | c | a | a | G | g | g | c | g | g | g | : | 6 | 0 | ||||||||
| 4 | r | e | c | o | v | e | r | e | d | : | G | c | a | g | a | T | A | m | g | G | a | w | g | g | t | k | t | t | c | t | a | c | a | a | a | t | a | g | a | g | c | g | t | m | T | m | C | c | a | s | k | t | g | a | A | t | a | c | t | a | m | s | a | g | g | g | c | g | k | G | : | 6 | 0 | |||||
| G | C | G | A | T | A | G | A | G | T | T | C | C | A | A | A | T | G | G | C | T | T | C | A | T | G | A | A | T | A | C | A | G | G | G | C | G | G |
| * | 8 | 0 | * | 1 | 0 | 0 | * | 1 | 2 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | t | t | a | c | g | c | c | g | c | c | g | c | g | a | t | c | t | t | c | G | c | g | c | c | g | a | t | c | c | a | t | t | a | a | C | c | c | t | t | G | t | t | g | a | a | c | g | t | t | g | g | c | t | c | t | G | t | c | a | g | : | 1 | 2 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | t | a | c | c | g | y | w | g | y | c | k | c | g | a | t | g | T | c | r | g | m | g | c | c | g | a | T | g | t | w | c | c | w | a | r | c | m | t | t | k | c | y | g | A | g | C | g | T | g | g | a | c | k | c | t | g | t | g | a | g | : | 1 | 2 | 0 | ||||
| T | C | G | G | C | C | G | A | T | T | G | G | C | C | G | A | T | A | C | T | T | G | A | C | G | T | G | C | C | T | G | T | A | G |
| * | 1 | 4 | 0 | * | 1 | 6 | 0 | * | 1 | 8 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | g | c | A | t | g | t | g | a | a | g | c | c | a | a | a | G | t | g | g | c | G | g | a | c | c | c | t | a | c | c | g | c | g | a | t | g | g | t | g | g | t | c | g | c | t | a | c | A | g | t | g | g | a | A | g | a | a | A | a | t | : | 1 | 8 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | t | C | A | t | c | t | a | a | s | c | m | C | a | a | A | g | t | g | g | c | g | g | w | a | C | c | t | g | t | y | t | c | g | k | t | g | g | t | g | g | T | c | g | a | a | a | y | w | g | c | g | m | t | a | g | c | g | a | a | c | : | 1 | 8 | 0 | ||||
| C | A | T | T | A | C | A | A | A | G | T | G | G | C | G | G | C | C | T | C | G | T | G | G | T | G | G | T | C | G | A | G | G | A | G | A | A |
| * | 2 | 0 | 0 | * | 2 | 2 | 0 | * | 2 | 4 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | g | g | t | c | a | G | c | c | t | t | a | t | c | a | g | c | g | c | a | t | G | g | t | t | t | C | a | c | t | c | a | a | a | c | a | t | t | a | c | g | A | c | g | a | a | a | a | a | g | T | c | a | t | g | g | t | g | t | t | t | : | 2 | 4 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | g | y | t | c | t | g | c | C | t | w | t | a | a | a | G | g | G | g | a | y | g | a | k | a | c | c | a | y | t | c | a | m | a | c | g | T | g | s | c | G | a | c | g | A | a | A | A | t | g | a | c | a | g | g | g | t | g | g | T | c | : | 2 | 4 | 0 | ||||
| G | T | C | G | C | C | T | A | G | G | A | G | C | A | T | C | A | A | C | T | C | G | A | C | G | A | A | A | A | G | C | A | G | G | T | G | T |
| * | 2 | 6 | 0 | * | 2 | 8 | 0 | * | 3 | 0 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | C | a | c | a | c | c | a | a | c | c | t | G | g | T | c | a | g | c | A | g | t | a | a | a | g | c | a | c | a | t | c | a | a | A | t | c | g | a | a | a | a | t | a | a | t | c | c | g | c | g | c | g | C | C | a | g | c | c | t | g | : | 3 | 0 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | c | a | c | a | g | m | a | a | g | y | c | y | g | a | a | a | g | a | a | g | t | w | a | t | k | c | t | c | g | t | g | a | A | a | t | a | t | a | t | a | a | t | a | a | t | c | c | g | c | g | c | g | c | c | A | a | t | w | t | c | : | 3 | 0 | 0 | ||||
| C | A | C | A | A | A | G | A | G | A | G | T | A | C | C | T | A | A | A | T | A | A | A | T | A | A | T | C | C | G | C | G | C | G | C | C | A | T |
| * | 3 | 2 | 0 | * | 3 | 4 | 0 | * | 3 | 6 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | c | t | g | t | t | c | c | c | g | t | g | g | A | a | t | a | c | c | c | t | t | g | a | g | c | g | c | c | a | g | g | t | g | a | t | g | g | t | g | G | t | c | g | g | t | a | a | a | g | c | a | g | a | a | c | g | C | c | t | t | : | 3 | 6 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | s | t | r | g | t | c | c | g | t | y | g | g | r | A | t | m | c | c | c | t | t | G | A | G | a | g | t | c | w | g | k | t | g | a | t | s | g | k | k | c | g | a | G | G | t | A | w | w | g | a | r | g | a | c | c | k | c | c | a | y | : | 3 | 6 | 0 | ||||
| T | T | C | C | G | G | A | T | C | C | C | T | T | G | A | G | G | C | G | T | G | A | T | G | G | G | T | A | G | G | A | C | C | C |
| * | 3 | 8 | 0 | * | 4 | 0 | 0 | * | 4 | 2 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | t | c | g | a | c | t | c | A | c | A | a | a | g | t | g | a | t | g | a | a | G | T | a | t | t | t | t | c | a | t | a | g | c | c | g | T | c | T | g | c | g | T | g | a | t | a | g | c | c | a | g | a | t | t | g | g | t | g | c | a | : | 4 | 2 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | k | s | a | a | s | T | c | t | c | a | a | w | g | t | a | a | t | a | c | a | g | t | r | t | t | t | t | m | a | c | a | g | s | g | g | t | c | t | a | c | t | t | g | a | t | w | g | t | c | a | g | a | T | T | g | t | t | g | c | a | : | 4 | 2 | 0 | ||||
| A | T | C | C | A | A | G | T | A | T | A | G | T | T | T | T | T | A | A | G | G | T | C | T | C | T | G | A | T | G | C | A | G | A | T | T | G | T | G | C | A |
| * | 4 | 4 | 0 | * | 4 | 6 | 0 | * | 4 | 8 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | t | g | g | g | t | t | t | c | g | a | C | C | c | a | g | t | c | c | a | g | t | c | g | c | a | t | t | t | C | t | g | c | c | c | g | c | g | g | t | G | t | c | c | t | t | g | a | a | G | g | t | a | a | a | t | t | c | c | t | g | : | 4 | 8 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | t | g | g | g | t | c | T | s | G | a | c | c | c | g | G | c | c | c | a | g | c | C | s | s | c | t | t | T | c | T | k | c | g | a | t | m | g | s | t | m | T | a | g | t | T | G | m | a | c | c | t | a | m | a | w | g | g | c | t | t | : | 4 | 8 | 0 | ||||
| T | G | G | G | T | T | G | A | C | C | C | G | C | C | A | G | C | T | T | T | C | T | C | G | T | T | T | T | G | A | T | A | A | C | T |
| * | 5 | 0 | 0 | * | 5 | 2 | 0 | * | 5 | 4 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | T | a | g | c | t | T | T | a | g | c | a | g | a | a | g | t | t | t | c | a | a | c | a | g | g | G | c | g | a | a | g | t | g | c | c | a | t | t | g | c | c | g | a | g | A | t | t | t | t | g | g | g | g | c | g | g | t | t | t | t | : | 5 | 4 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | r | r | a | c | a | s | t | A | g | c | a | m | c | m | s | t | y | a | c | g | a | c | c | g | g | g | s | c | c | c | y | t | k | a | s | a | t | g | g | c | c | g | w | c | a | t | r | t | w | g | g | g | g | c | g | r | t | a | T | a | : | 5 | 4 | 0 | ||||
| C | 3 | T | A | G | C | A | T | C | A | C | G | G | G | T | A | T | G | C | C | G | A | T | T | G | G | G | G | C | G | T | T |
| * | 5 | 6 | 0 | * | 5 | 8 | 0 | * | 6 | 0 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | c | g | c | g | t | c | a | g | c | c | t | t | g | a | a | c | T | g | a | t | t | g | G | g | T | t | c | t | g | g | c | a | g | g | g | t | g | C | t | A | a | T | c | a | t | c | g | c | c | t | g | c | a | G | g | a | c | c | g | c | : | 6 | 0 | 0 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | c | r | t | c | t | c | a | g | c | C | t | g | g | a | a | c | t | g | A | t | t | g | A | t | w | a | y | t | c | w | c | a | g | g | y | y | g | c | c | a | a | y | c | t | c | g | r | c | g | t | g | c | c | k | g | r | s | c | a | g | : | 6 | 0 | 0 | ||||
| C | T | C | A | G | C | C | T | G | A | A | C | T | G | A | T | T | G | T | C | A | G | G | G | C | A | A | C | C | T | G | C | G | C |
| * | 6 | 2 | 0 | * | 6 | 4 | 0 | * | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b | u | n | d | l | e | 1 | : | t | t | t | t | G | g | t | a | c | c | a | g | c | g | t | g | a | A | a | a | t | g | G | t | g | c | g | t | g | g | a | a | g | a | t | t | g | a | t | c | g | t | T | t | t | g | c | a | c | c | c | : | 6 | 5 | 1 | |||||||
| 4 | r | e | c | o | v | e | r | e | d | : | t | A | T | t | t | t | t | a | m | c | a | g | m | c | k | G | A | a | g | A | y | g | r | t | g | C | t | g | g | g | c | r | g | a | t | s | g | a | w | c | c | t | c | t | t | c | c | a | c | a | s | : | 6 | 5 | 1 | ||||
| T | T | T | T | A | C | A | G | G | A | A | A | G | T | G | C | G | G | G | A | T | 3 | G | A | C | T | T | T | C | A | C |