Задание 1.
| Название | Мнемоника |
| Bacillus anthracis | BACAN |
| Bacillus subtilis | BACSU |
| Clostridium tetani | CLOTE |
| Finegoldia magna | FINM2 |
| Lactobacillus acidophilus | LACAC |
| Lactobacillus delbrueckii | LACDA |
| Lactococcus lactis | LACLM |
| Streptococcus pneumoniae | STRPN |
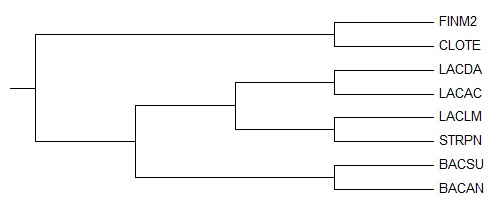
скобочная формула: ((FINM2,CLOTE),(((LACDA,LACAC),(LACLM,STRPN)),(BACSU,BACAN)))
список нетривиальных ветвей как разбиений множества листьев:
1) {FINM2, CLOTE} vs {LACDA, LACAC, LACLM, STRPN, BACSU, BACAN}
2) {LACDA, LACAC} vs {FINM2, CLOTE, LACLM, STRPN, BACSU, BACAN}
3) {LACLM, STRPN} vs {FINM2, CLOTE, LACDA, LACAC, BACSU, BACAN}
4) {BACSU, BACAN} vs {FINM2, CLOTE, LACDA, LACAC, LACLM, STRPN}
5) {LACDA, LACAC, LACLM, STRPN} vs {FINM2, CLOTE, BACSU, BACAN}
Занятие 2.
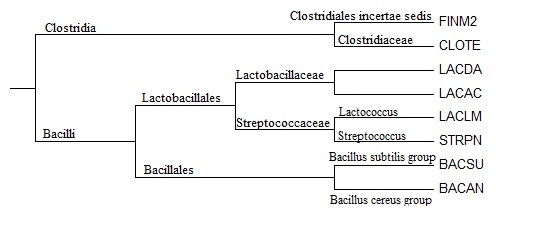
Файл с таксономией отобранных бактерий. Соответствуещее ему изображение:
Для белка, ответственного за фактор элонгации трансляции G, с мнемоникой EFG получены fasta-последовательности (seqret @data.list protein.fasta). Соответствующие data.list и protein.fasta . Выполнено выравнивание белков программой muscle (muscle -in protein.fasta -out protein.afa): выходной файл . Далее выполнен поиск диагностических позиций.
Была выполнена реконструкция дерева программой fprotpars( fprotpars aligprot.fasta -outtreefile prot.treefile -outfile prot.fprotpars).
Программа выдала единственное дерево со скобочной формулой:
(((((STRPN,LACLM),(BACSU,BACAN)),(LACDA,LACAC)),CLOTE),FINM2)
и изображением:
+--STRPN
+-----7
! +--LACLM
+-----6
! ! +--BACSU
! +-----5
+--4 +--BACAN
! !
! ! +--LACDA
+--2 +-----------3
! ! +--LACAC
1 !
! +-----------------CLOTE
!
+--------------------FINM2
Изображение, полученное по скобочной формуле, программой MEGA:
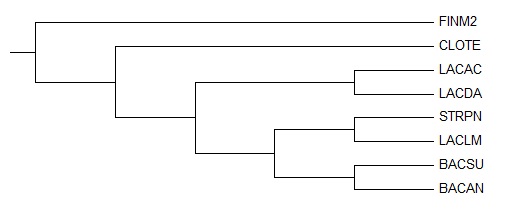
В нем присутствуют 4 нетривиальные ветви:
1){LACDA, LACAC} vs {FINM2, CLOTE, LACLM, STRPN, BACSU, BACAN}
2){BACSU, BACAN} vs {FINM2, CLOTE, LACDA, LACAC, LACLM, STRPN}
3){LACLM, STRPN} vs {FINM2, CLOTE, LACDA, LACAC, BACSU, BACAN}
4){LACLM, STRPN, BACSU, BACAN} vs {FINM2, CLOTE, LACDA, LACAC}
5){FINM2, CLOTE} vs {LACDA, LACAC, LACLM, STRPN, BACSU, BACAN}
Три первые ветви идентичны ветвям первоначально данного дерева, четвертой же ветви в нем нет. В полученном дереве отсутствуют ветвь:
{LACDA, LACAC, LACLM, STRPN} vs {FINM2, CLOTE, BACSU, BACAN}
Матрица эволюционных расстояния между последовательностями, определенная программой fprotdist (fprotdist aligprot.fasta -outfile prot.fprotdist).
---- FINM2 CLOTE LACAC LACDA BACAN BACSU LACLM STRPN
FINM2 0.000000 0.428674 0.571581 0.580823 0.399675 0.431713 0.502799 0.495805
CLOTE 0.428674 0.000000 0.523409 0.526650 0.398823 0.402294 0.530544 0.487279
LACAC 0.571581 0.523409 0.000000 0.104058 0.390270 0.375519 0.362138 0.367766
LACDA 0.580823 0.526650 0.104058 0.000000 0.389968 0.378074 0.370815 0.375282
BACAN 0.399675 0.398823 0.390270 0.389968 0.000000 0.133616 0.291700 0.235468
BACSU 0.431713 0.402294 0.375519 0.378074 0.133616 0.000000 0.307128 0.275347
LACLM 0.502799 0.530544 0.362138 0.370815 0.291700 0.307128 0.000000 0.146447
STRPN 0.495805 0.487279 0.367766 0.375282 0.235468 0.275347 0.146447 0.000000
Рассмотрим свойство ультраметричности на двух примерах:
1) Возьмем три объекта: LACAC, LACDA, LACLM:
---- LACAC LACDA LACLM
LACAC 0.000000 0.104058 0.362138
LACDA 0.104058 0.000000 0.370815
LACLM 0.362138 0.370815 0.000000
видно, что d(LACAC, LACLM)=d(LACLM, LACDA)>d(LACAC, LACDA). Свойство ультраметричности выполняется.
При этом, (d(LACLM, LACDA)- d(LACAC, LACLM))/d(LACAC, LACLM)= 0,02396 - относительная ошибка, когда мы учитываем, что эти расстояния равны, достаточно мала.
2) Возьмем три объекта: FINM2, BACAN, STRPN:
---- FINM2 BACAN STRPN
FINM2 0.000000 0.399675 0.495805
BACAN 0.399675 0.000000 0.235468
STRPN 0.495805 0.235468 0.000000
видно, что d(BACAN, FINM2) не равно d(STRPN, FINM2), но оба расстояния > d(BACAN, STRPN). Свойство ультраметричности не выполняется.
Рассмотрим свойство аддитивности на примере LACAC, LACDA, BACSU, LACLM:
---- LACAC LACDA BACSU LACLM
LACAC 0.000000 0.104058 0.375519 0.362138
LACDA 0.104058 0.000000 0.378074 0.370815
BACSU 0.375519 0.378074 0.000000 0.307128
LACLM 0.362138 0.370815 0.307128 0.000000
Оценим расстояния:
d(LACAC, LACDA)+d(BACSU,LACLM)= 0,411186 =x
d(LACDA, LACLM)+d(LACAC,BACSU)= 0,746334 =y
d(LACDA, BACSU)+d(LACAC,LACLM)= 0,740212 =z
Таким образом, y=z>x - свойство аддитивности выполняется. При этом разница между двумя примерно равными суммами растояний - лищь в третем знаке после запятой.
Получим две реконструкции дерева программой fneighbor, используя два алгоритма: UPGMA и Neighbor-Joining.
Neighbor-joining method UPGMA method
+-----------CLOTE +------------FINM2
! +-6
! +--LACAC ! +------------CLOTE
! +---------1 !
! ! +---LACDA --7 +--LACAC
! +--4 ! +--------1
! ! ! +----LACLM ! ! +--LACDA
! ! +---3 ! !
2----5 +--STRPN +--5 +---BACAN
! ! ! +----2
! ! +--BACAN ! ! +---BACSU
! +--6 +--4
! +---BACSU ! +----LACLM
! +---3
+------------FINM2 +----STRPN
Нетривиальные ветви: Нетривиальные ветви:
1) {LACAC, LACDA}vs{FINM2, CLOTE, LACLM, STRPN, BACSU, BACAN} 1) {LACAC, LACDA}vs{FINM2, CLOTE, LACLM, STRPN, BACSU, BACAN}
2) {LACLM, STRPN}vs{FINM2, CLOTE, LACDA, LACAC, BACSU, BACAN} 2) {LACLM, STRPN}vs{FINM2, CLOTE, LACDA, LACAC, BACSU, BACAN}
3) {BACAN, BACSU}vs{FINM2, CLOTE, LACDA, LACAC, LACLM, STRPN} 3) {BACAN, BACSU}vs{FINM2, CLOTE, LACDA, LACAC, LACLM, STRPN}
4) {LACAC, LACDA, LACLM, STRPN}vs{FINM2, CLOTE, BACSU, BACAN} 4) {FINM2, CLOTE}vs{LACDA, LACAC, LACLM, STRPN, BACSU, BACAN}
5){FINM2, CLOTE}vs{LACDA, LACAC, LACLM, STRPN, BACSU, BACAN} 5) {BACAN, BACSU, LACLM, STRPN}vs{FINM2, CLOTE, LACDA, LACAC}
Все из вышеперечисленных ветвей этого неукорененного дерева В данном случае только первые 4 ветви удовлетворяют
присутствовали в первоначально данном дереве. правильному первоначальному дереву. Однако, как и в случае с fprotpars
находится та же лишняя №5 ветвь, но нет правильной
{LACAC, LACDA, LACLM, STRPN}vs{FINM2, CLOTE, BACSU, BACAN}.
В целом, всеми 3 способами верно определялось разбиение на 3 пары. Таким образом, наиболее близким к исходному,но неукорененным является дерево, созданное по алгоритму Neighbor-joining.