Модель для эксперимента и создание функции
Для выполнения задания была выбрана модель, состоящая из трех молекул, связанных водородными связями. Описание модели представлено в статье [1]. Изображение модели показано на рисунке 1.

Рисунок 1. Модель взаимодействующих молекул, использованная для построения функции электронной плотности. Изображение из статьи [1].
Скрипт compile-func.py задает гауссову функцию на интервале [0,30], которая определяется числами lambda, beta, gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). Функция задается в виде суммы гармоник. Параметр lambda отвечает за высоту пика (зависит от числа электронов в атоме), beta отвечает за ширину гармоники, а gamma определяет положение максимума. Функция для указанной модели задана с помощью скрипта compile-func.py:
>python compile-func.py -g 2,3,5+20,2,6.5+2,2,8+2,3,10.5+40,2.5,11.6+40,2.5,13+2,3,14.1
Так был получен график функции funk1.txt.
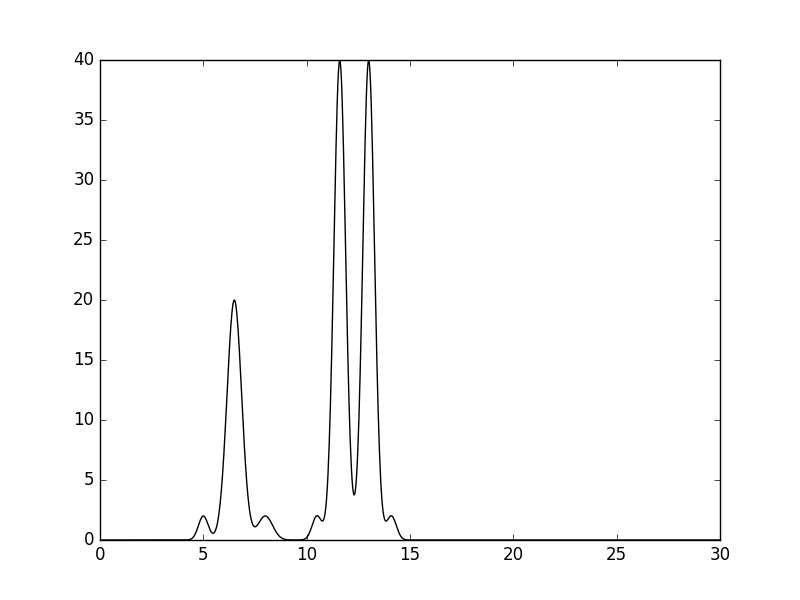
Рисунок 2. График функции funk1.txt, который отражает заданное вручную распределение электронной плотности в модели BeH2--C2H2.
Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Файл с коэффициентами Фурье fourier1.txt был получен с помощью скрипта func2fourier.py в нём записаны номер каждой гармоники, её амплитуда и фаза.
>python func2fourier.py -i func1.txt -o fourier1.txt
Поиск минимального набора гармоник, необходимого для отличного восстановления функции
Далее с помощью скриптаfourier2func.py была полностью восстанослена изначальная функция по полному набору гармоник (всего 498 гармоник). Её график полностью совпадает с изначальной функцией (рисунок 3).

Рисунок 3. График функции, восстановленной по полному набору гармоник.
Чтобы определить минимальный необходимый для восстановления функции набор гармоник (n_0), использовался скрипт fourier-filter.py. При построении функции по гармоникам 0-25 можно различить атомы водорода, но они еще немного сливаются с шумом. Для гармоник 0-30 восстановление безупречное, считаем, что это n_0. Стоит отметить, что пики на графике 0-30 разделены сильнее, чем на графике исходной функции.
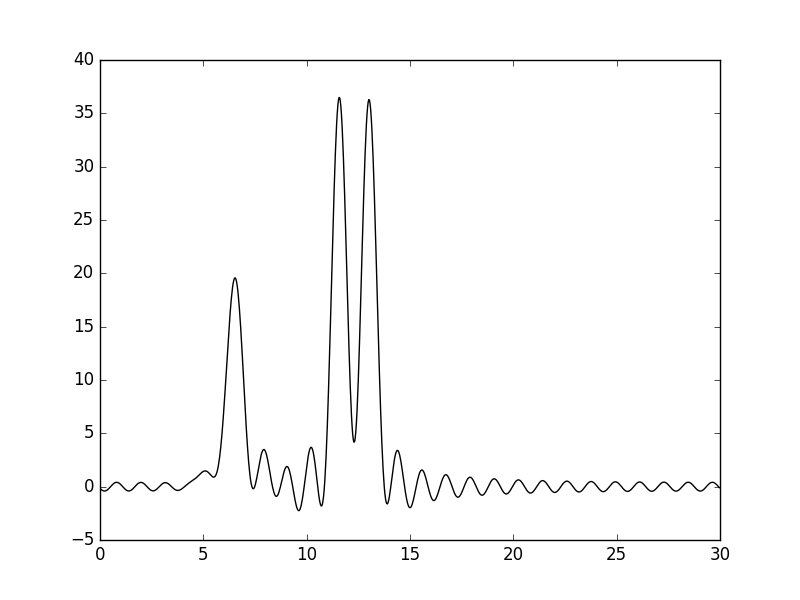
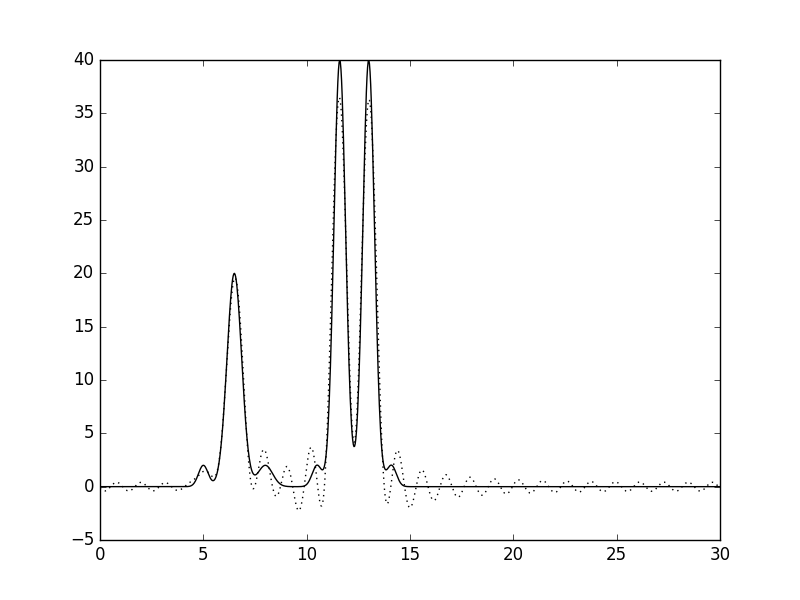
Рисунки 4 и 5. График функции, восстановленной по гармоникам 0-25, и его наложение (пунктир) на график исходной функции.
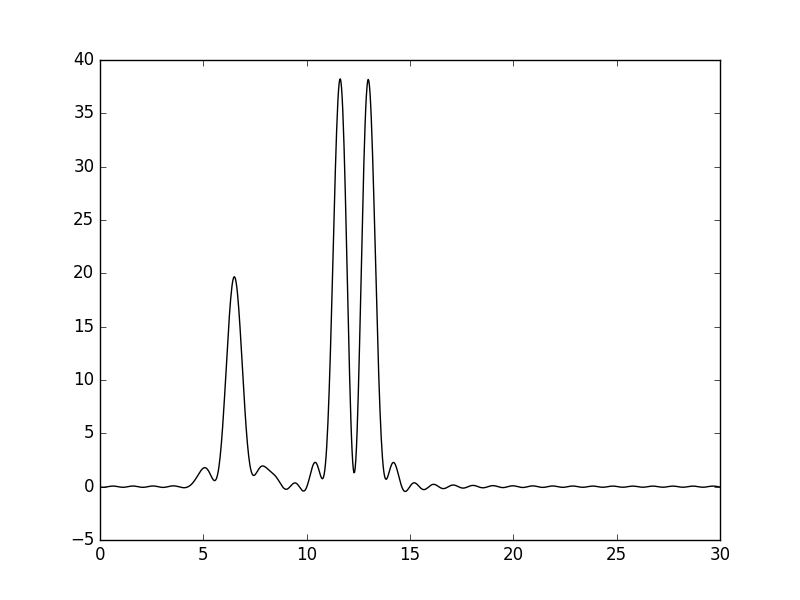
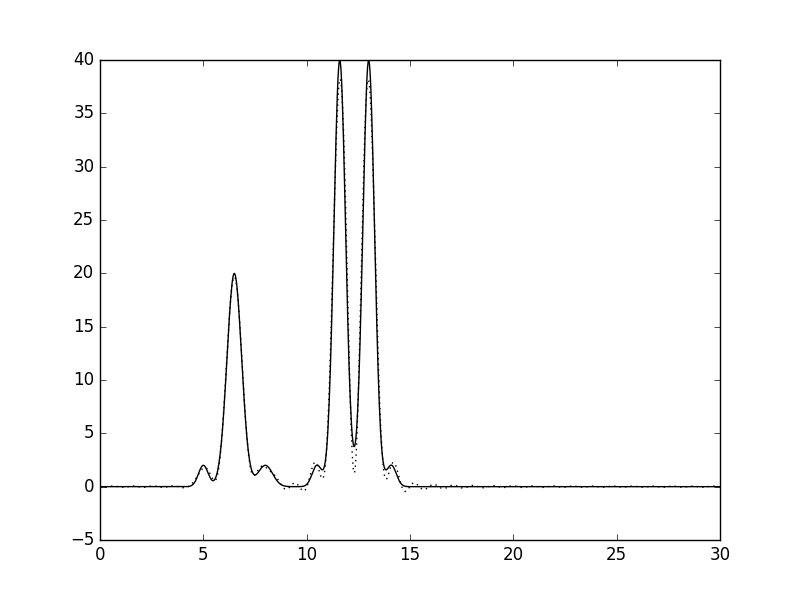
Рисунки 6 и 7. График функции, восстановленной по гармоникам 0-30, и его наложение (пунктир) на график исходной функции.
Восстановление функции по гармоникам 0-15 даёт представление о расположении отдельных атомов, отличных от атомов водорода.
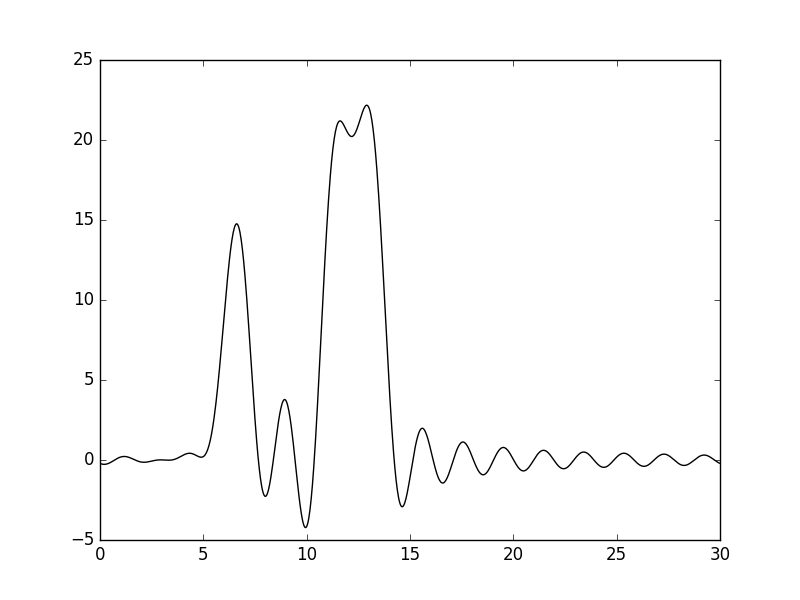
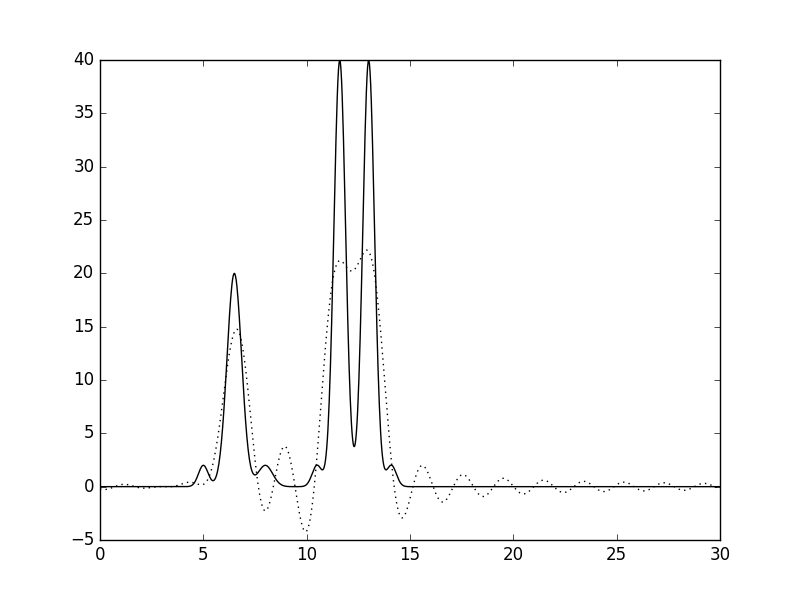
Рисунки 8 и 9. График функции, восстановленной по гармоникам 0-15, и его наложение (пунктир) на график исходной функции.
Восстановление функции по гармоникам 0-5 даёт представление о расположении атомов, отличных от атомов водорода, однако не позволяет различить отдельные атомы.
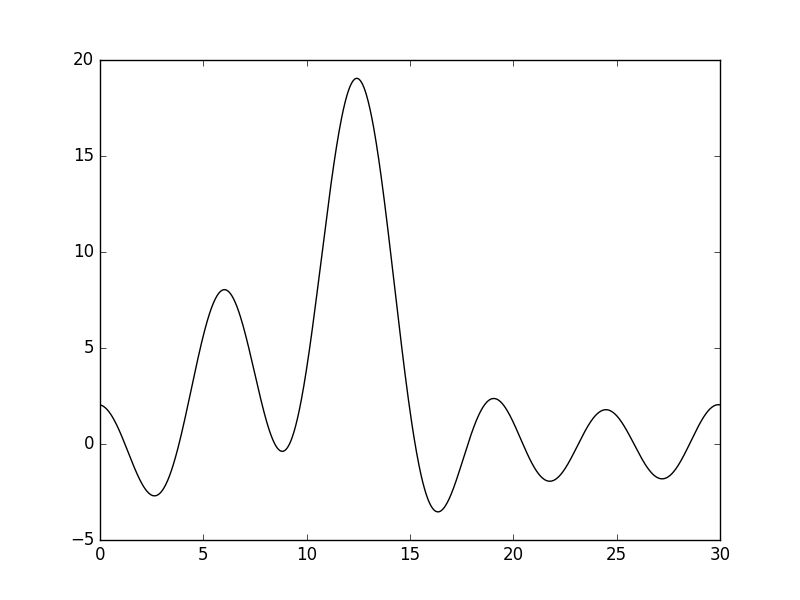
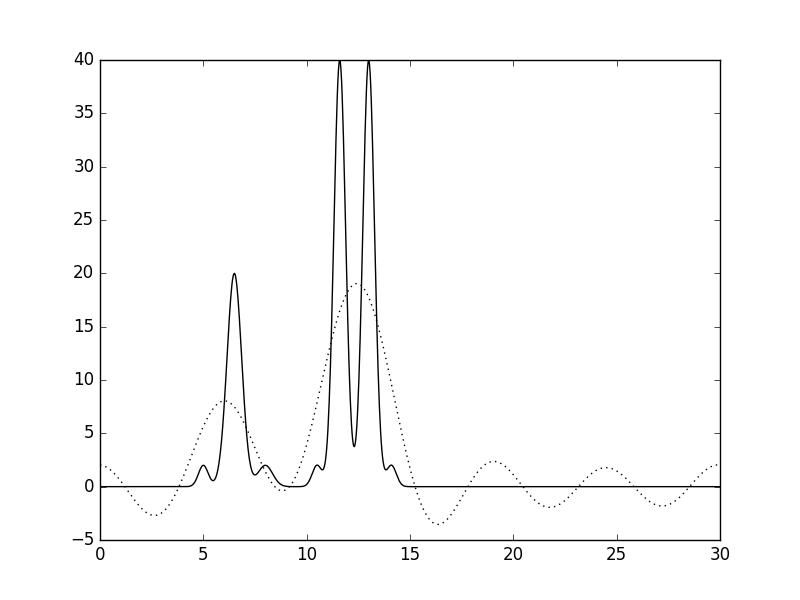
Рисунки 10 и 11. График функции, восстановленной по гармоникам 0-5, и его наложение (пунктир) на график исходной функции.
Влияние шума на восстановление функции электронной плотности
Добавление шума в 20% к амплитудам ухудшает восстановление по гармоникам 0-30. Различить атомы водорода уже сложно (в принципе, они видны, только как понять, что это не шум, если у нас нет исходных данных). Это хорошее восстановление.

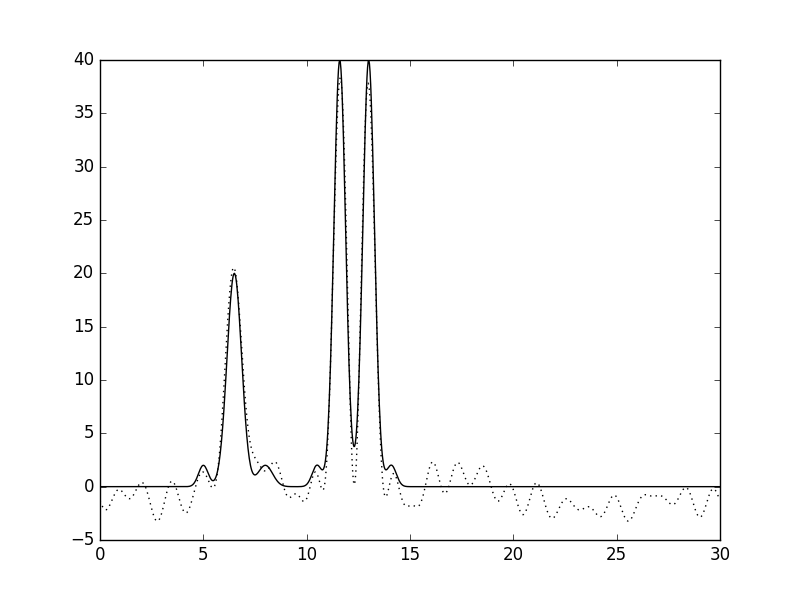
Рисунки 12 и 13. График функции, восстановленной по гармоникам 0-30 с добавлением шума к амплитудам в 20%, и его наложение (пунктир) на график исходной функции.
Добавление шума в 20% к фазам ухудшает восстановление по гармоникам 0-30 сильнее, чем добавление шума к амплитудам. Различить атомы водорода сложно.
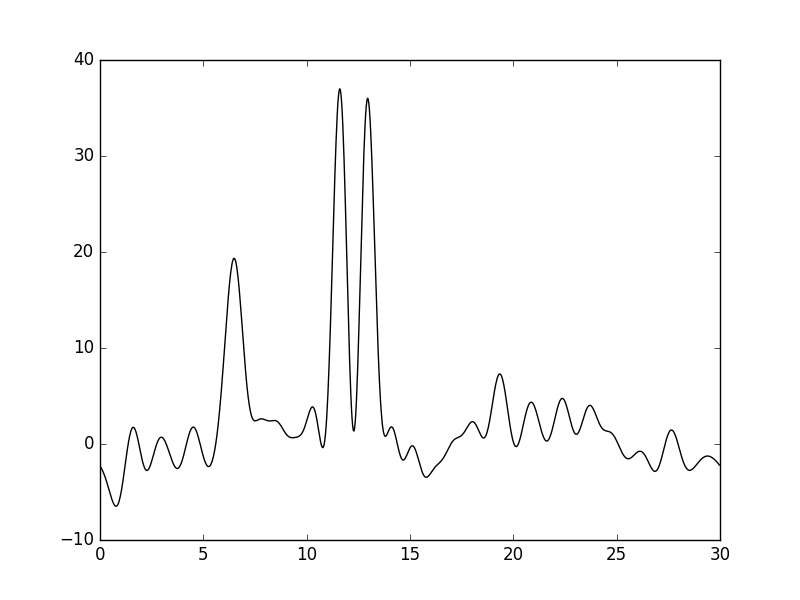

Рисунки 14 и 15. График функции, восстановленной по гармоникам 0-30 с добавлением шума к фазам в 20%, и его наложение (пунктир) на график исходной функции.
При добавлении шума в 20% и к амплитудам, и к фазам восстановление по гармоникам 0-30 ухудшается. Атомы водорода неразличимы.

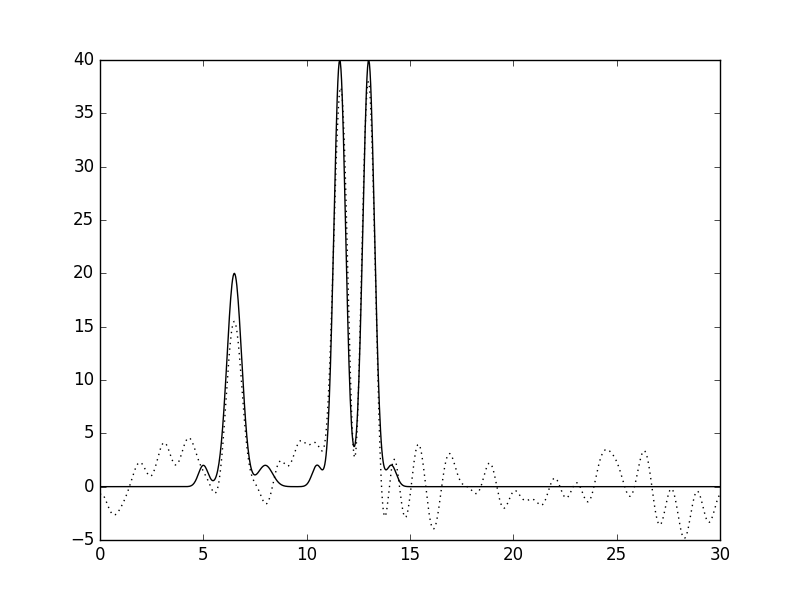
Рисунки 16 и 17. График функции, восстановленной по гармоникам 0-30 с добавлением шума и к амплитудам, и к фазам в 20%, и его наложение (пунктир) на график исходной функции.
При добавлении шума в 10% и к амплитудам, и к фазам восстановление по гармоникам 0-30 позволяет определить не все атомы водорода.
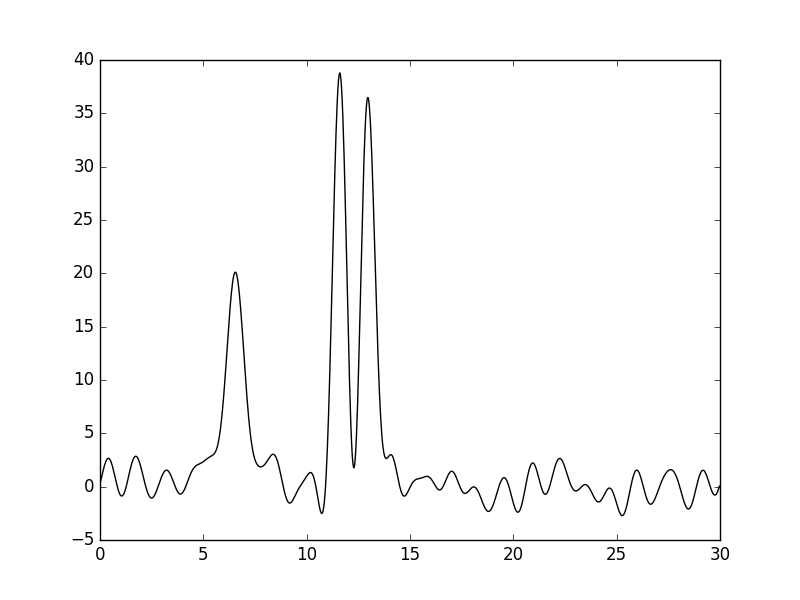
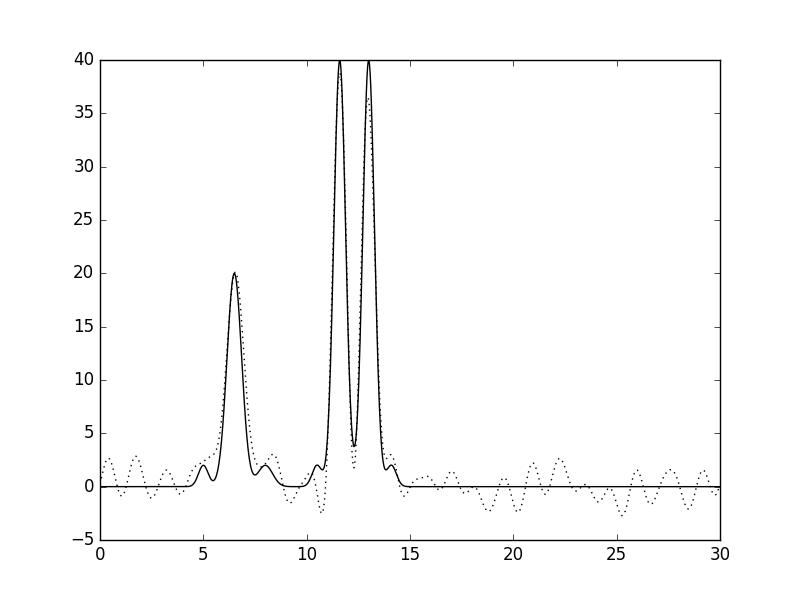
Рисунки 18 и 19. График функции, восстановленной по гармоникам 0-30 с добавлением шума и к амплитудам, и к фазам в 10%, и его наложение (пунктир) на график исходной функции.
Неполные наборы гармоник
Удаление первых пяти гармоник не сильно влияет на качество графика функции электронной плотности. Различимы даже атомы водорода, однако график целиком сильно меняет свое положение. При удалении первых десяти гармоник атомов водрода не различить, и появляется отрицательный пик с большой амплитудой. На рисунке 20 для функкции, восстановленной по гармоникам 1-30 видно, что график просто сдвинут вниз. Это объясняется тем, что нулевая гармоника - это константа.
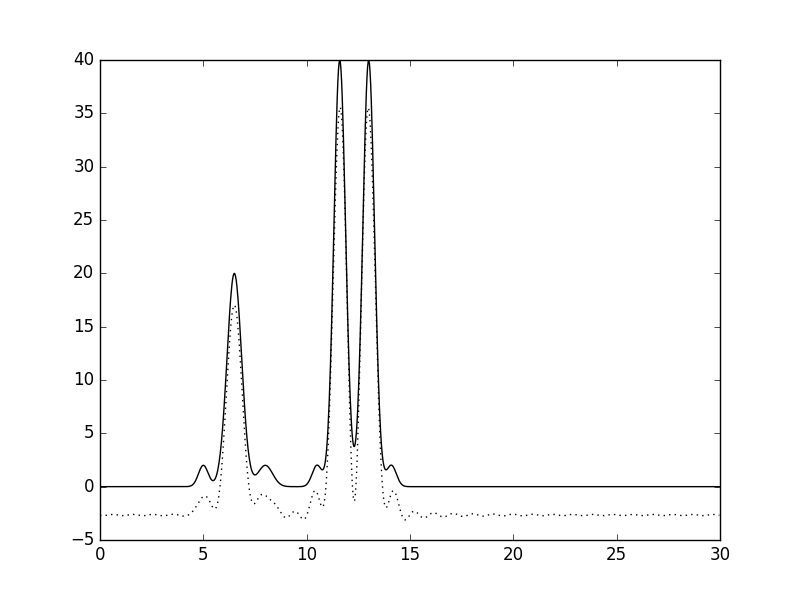
Рисунок 20. График функции, восстановленной по гармоникам 1-30 (пунктир) в сравнении с графиком исходной функции (сплошная линия).
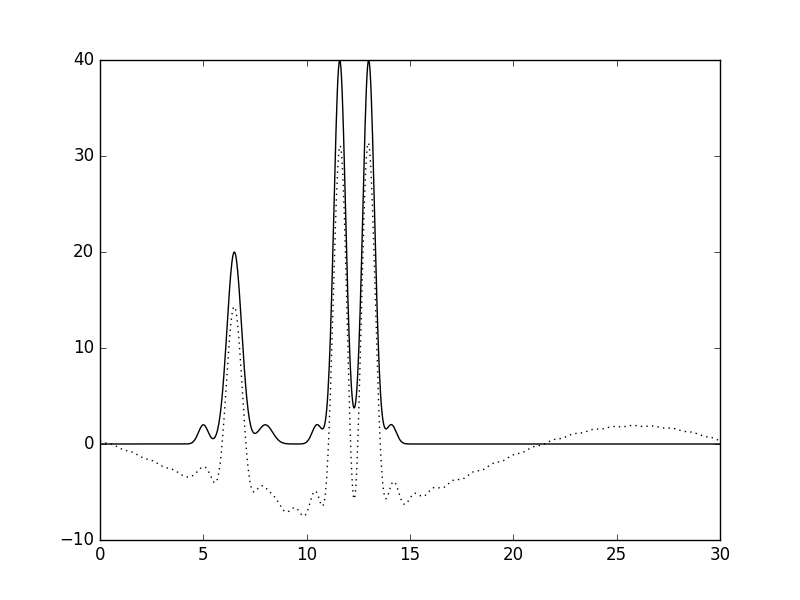
Рисунок 21. График функции, восстановленной по гармоникам 2-30 (пунктир) в сравнении с графиком исходной функции (сплошная линия).
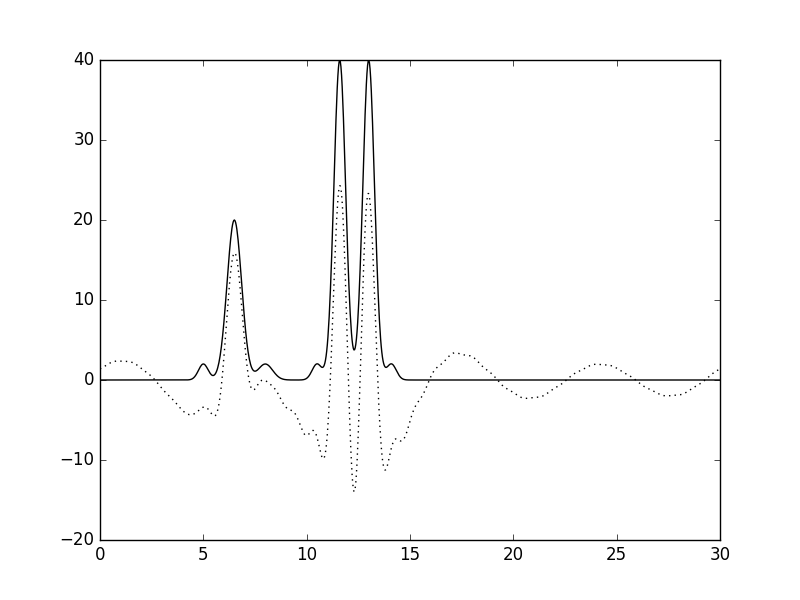
Рисунок 22. График функции, восстановленной по гармоникам 5-30 (пунктир) в сравнении с графиком исходной функции (сплошная линия).
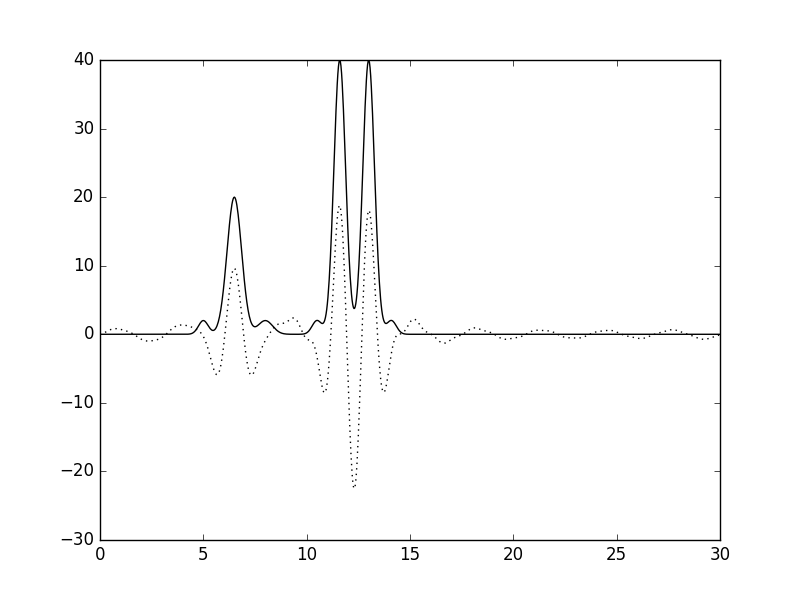
Рисунок 23. График функции, восстановленной по гармоникам 10-30 (пунктир) в сравнении с графиком исходной функции (сплошная линия).
Удаление гармоник 15 и 16 не привело к сильному ухудшению качества графика. Его даже можно оценить как отличное, потому что атомы водорода можно различить.
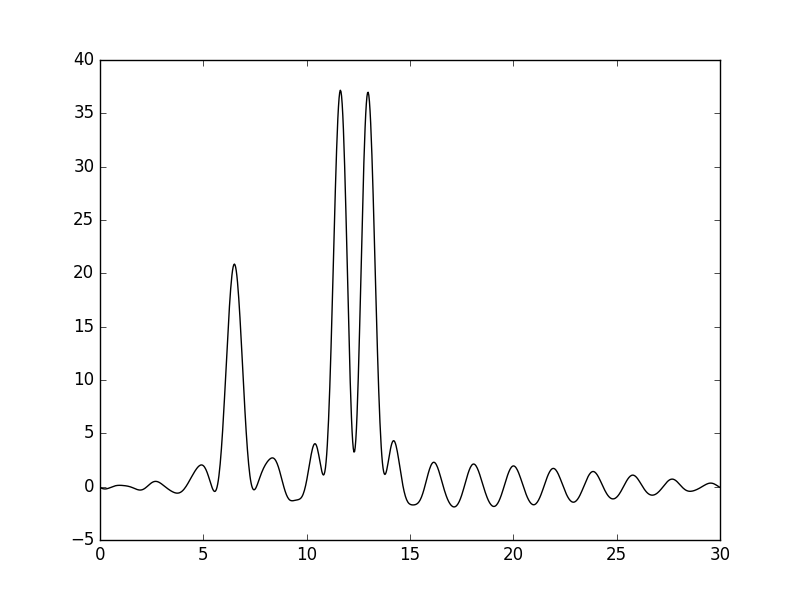
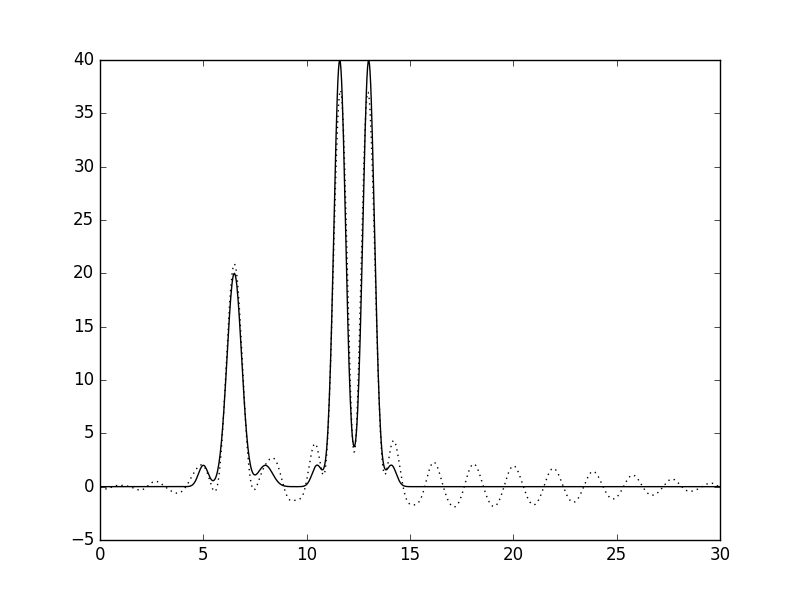
Рисунки 24 и 25. График функции, восстановленной по гармоникам 0-14, 17-30, и его наложение (пунктир) на график исходной функции.
Добавление гармоники 40 привело к усилению колебаний на "прямой части" графика функции. Кроме того, эта гармоника не улучшает разрешение графика функции по-сравнению с графиком для функции, построенной по гармоникам 0-30, а скорее вносит неточности. Потому что на новом графике теперь можно подумать, что следом за атомом бериллия идут два водорода.
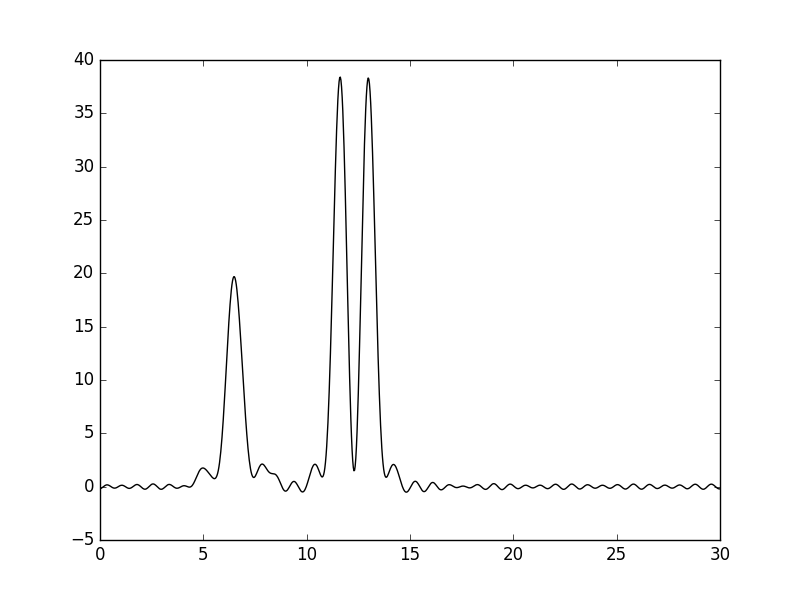
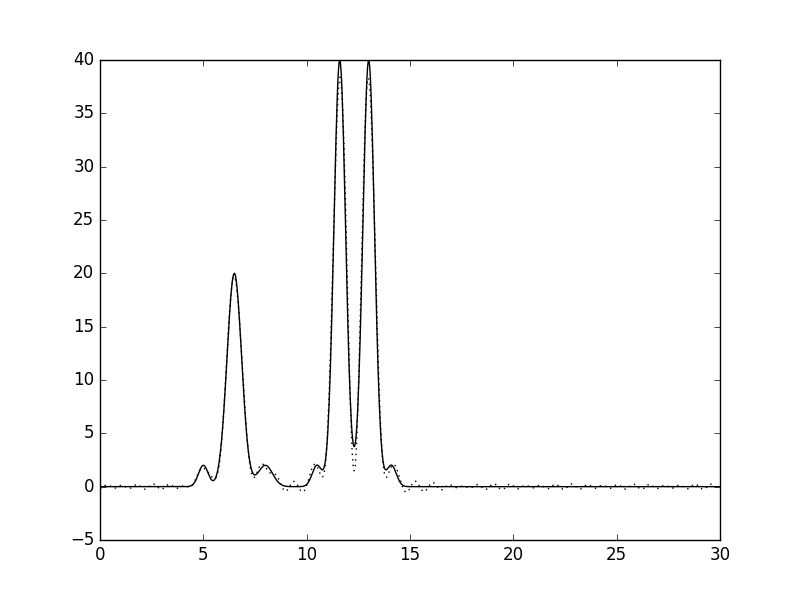
Рисунки 26 и 27. График функции, восстановленной по гармоникам 0-30, 40, и его наложение (пунктир) на график исходной функции.


Рисунки 28 и 29. График функции, восстановленной по гармоникам 0-30, и его наложение (пунктир) на график исходной функции.
Определение разрешения полученных графиков электронной плотности
Для полного набора гармоник (присутствуют все гармоники от 0 до n) разрешение определяется просто - это "длина волны" (период) гармоники n. В этом задании для полного набора гармоник 0-30 разрешение составляет 1 Å. В рассматриваемой модели нет элементов, находящихся на расстоянии меньше 0.5 Å, чтобы можно было проверить, различимы ли они при данном разрешении. Для графика функции, восстановленной по гармоникам 0-15, рарешение составляет 2 Å. Атомы водорода в модели находятся на расстоянии 1.1 Å от атомов углерода, их не получается отличить (в том числе и из-за шума). Однако на этом же графике различимы атомы углерода, которые находятся на расстоянии 1.4 Å. Впринципе, утверждение, что при разрешении d различимы детали, находящиеся на расстоянии больше d/2 справедливо, но оно зависит также и от амплитуды пиков, которые соответствуют этим атомам.
Для неполного набора гармоник при определении разрешения необходимо всегда указывать полноту, при которой оно определяется. Экспериментальные данные всегда представлены неполным набором, поэтому полнота данных является для них обязательным параметром.
Рассмотрим набор гармоник 2-30. Представлены длины волн от 1 Å до 15 Å. Этот набор содержит 29 гармоник с "длиной волны" больше (или равной) 1 Å. В полном наборе была бы 31 гармоника. Таким образом, определяем разрешение как 1 Å при полноте данных 93.5% (29/31 = 0.935).
Для набора 0-30, 40 разрешение можно определить двумя способами: это либо 1 Å при полноте 100%, либо 0.75 Å при полноте 78%.
Подробная характеристика всех построенных функций представлена в таблице.
Список литературы
1. De Oliveira B. G. (2013) Structure, energy, vibrational spectrum, and Bader’s analysis of π···H hydrogen bonds and H(-π)···H(+π) dihydrogen bonds., Phys. Chem. Chem. Phys., 15, 37–79.