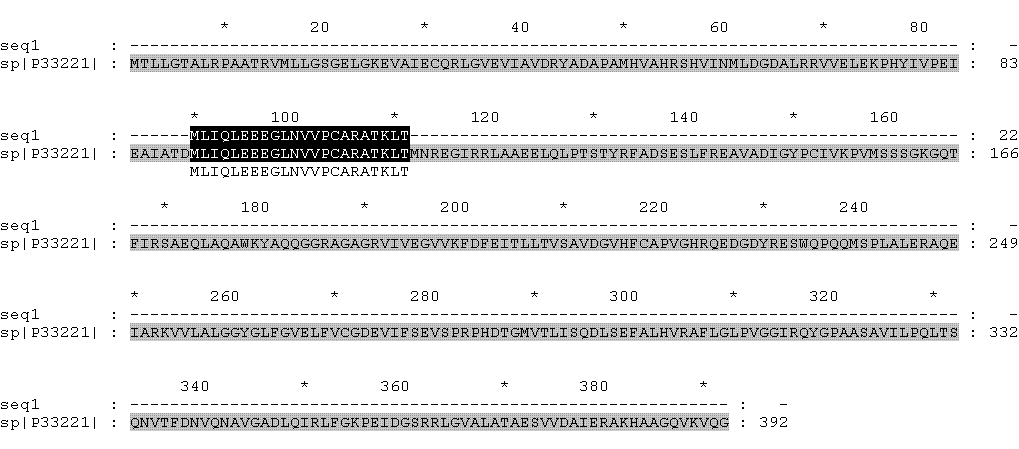
Пробное выравнивание
Последовательность >seq1 MLIQLEEEGLNVVPCARATKLT соответствует позициям 90 - 111 в полной последовательности белка PURT_Ecoli (код доступа P33221 в базе данных UniProt ) (запись в fasta-формате аминокислотной последовательности белка PURT_ECOLI )

Выравнивание последовательностей seq1 и seq2:
>seq1 MLIQLEEEGLNVVPCARATKLT
>seq2
DELVRIEQEGLATVVPTARATQ
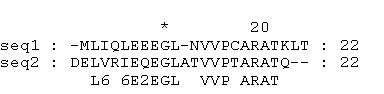
Исходная длина фрагментов - 22 а.о., длина выравнивания - 24, число совпавших аминокислотных остатков - 12.Найдем вес выравнивания, цена 1 совпадения аминокислотных остатков=1, цена любого проруска=-2, краевые пропуски не штрафуются W=1+1+3+3+4-2=10, процент идентичности последовательностей = (12/24)*100%=50%
На 4-ой позиции выравнивания, мы наблюдаем первую близкородственную замену аминокислотных остатков: в последовательности seq1 аминокислота I (изолейцин) (на 3 позиции в фрагменте seq1) заменена на аминокислоту V (валин) (на 4-ой позиции в фрагменте seq2), вес такой замены, согласно матрице BLOSUM62 = 3.
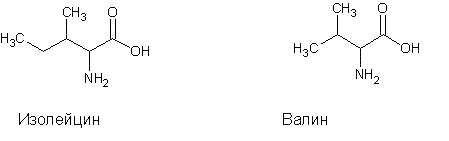
Боковые группы обеих аминокислот гидрофобны, незаряжены, разветвлены, длина их отличается только на -(СН2)- группу, поэтому такие аминокислоты близкородственны. Матрица BLOSUM62 симметрична, относительно главной диагонали, поэтому можно пользоваться только той ее частью, что над/под диагональю и самой диагональю.
Определим процент сходства:
Отношение числа сходных а.о. к общей длины выравнивания (17/24)*100%=70,8%, сходными аминокислотными остатками считаем те, замена которых имеет положительную цену по матрице BLOSUM62.

Подсчет цены замены аминокислотных остатков типа "W-Y" с помощью матрицы BLOSUM62 и Excel:
Таблица подсчета позволяет с помощью формул Excel найти вес выравнивания последовательностей.
В матрице BLOSUM62 на пересечении i-ой строки и j-го столбца стоит вес замены i-ой аминокислоты на j-ую, поэтому, сопоставив аминокислотные остатки в сравниваемых последовательностях со столбцами и строками таблицы, мы найдем цену замены одного а.о. на другой. На примере seq1 и seq2: скачать таблицу
Описание к таблице:
В столбец A, начиная с ячейки A32, впишем 1-ую последовательность, а в столбец B с B32 - 2-ую последовательность. Будем искать цену замены, по матрице, расположенной снизу справа. В столбец C с ячейки C32 впишем номер N1 - номер столбца, соответсвующего а.о. seq1, в верхней таблице, аналогичнч для столбца D: N2 - номер строки, соответсвующей а.о. seq2, в верхней таблице. N1 и N2 ищем с помощью функции ПОИСК, определяя номер а.о. в строчке а.о. (в ячейке A24). Ячейку с ценой замены, соответсвуюшую N1 и N2, определяем с помощью функции ГПР, но она спаршивает вначале номер столбца в таблице - цифру, поэтому сделаем еще одну таблицу - нижнию, где столбцы пронумированы, дополнительная же строка - нумеровка столбцов - учитывается прибавлением к N2 1, это число и спрашивает функция, ища строку. По строке и столбцу однозначно определяется вес замены (в столбце E).
В таблце также поместил формулы для расчета % сходства выровненных последовательностей (из предыдущего задания).
Другое выравнивание seq1 и seq2:
Скачать таблицу определения веса для этого выравнивания
Как видно из таблицы, первое выравнивание лучше: больше его вес 47>36, % сходства выровненных фрагментов также больше в первом случае 71%>64%.