Сравнение выравнивания одних и тех же последовательностей тремя разными программами

Для выравнивания были выбраны белки из 5 пункта 9 практикума: SYQ_HUMAN;SYQ_YERPY;SYQ_RAT;SYQ_SALEP;SYQ_ECOLI. В качестве программ для выравнивания были выбраны следующие 3 программы: MUSCLE, MAFFT, T-Coffee.

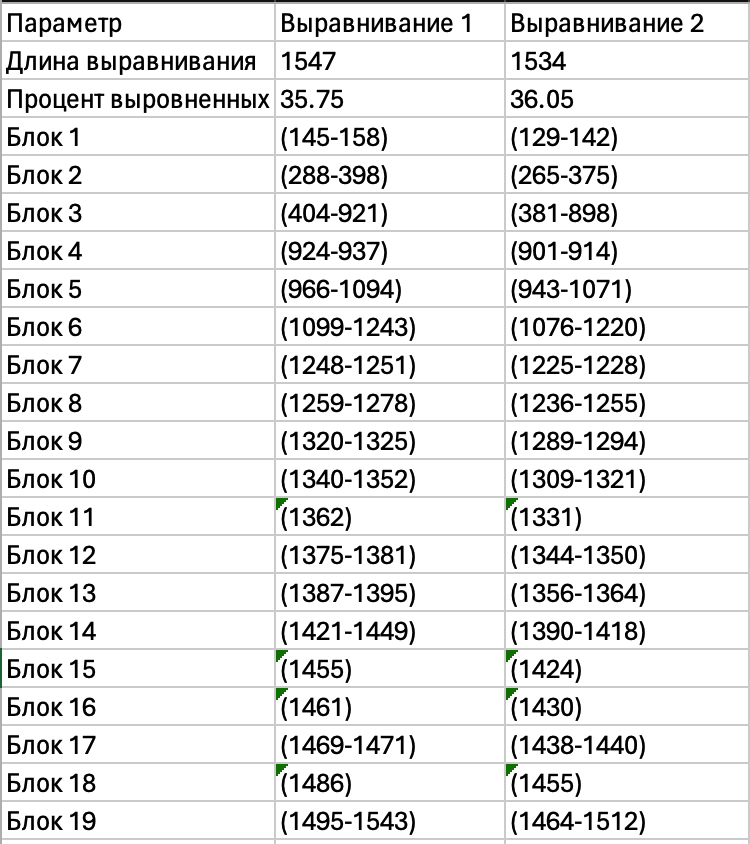
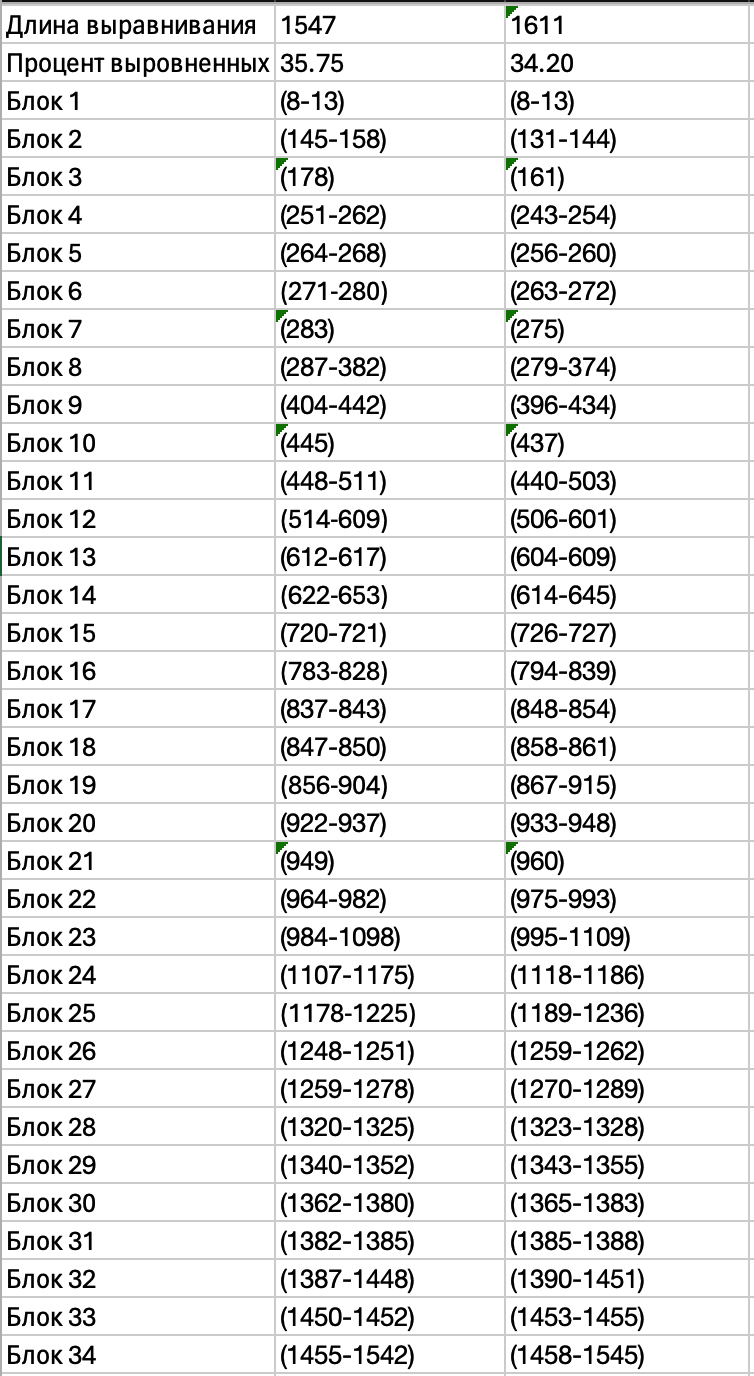
Общая длина достоверных колонок в выравнивании MAFFT - MUSCLE меньше, чем в выравнивании MAFFT - T-Coffee. Из этого можно сделать вывод, что выравнивания MAFFT with Defaults и T-Coffee with Defaults более схожи, чем MAFFT with Defaults и MUSCLE with defaults. Это может означать, что программы выравнивания TCOFFEE и MAFFT имеют более схожий алгоритм работы, чем MAFFT и MUSCLE.

Выравнивание Mafft
Выравнивание Muscle
Выравнивание Tcoffee

Построение выравнивания по совмещению структур и сравнение его с выравниванием MSA

Для проведения 3D выравнивания было выбрано следующее семейство доменов из Pfam: PF00078. Выравнивались следующие три белка: 1c0t, 1c0u, 1c1b.

Пространственное выравнивание осуществлялось с помощью Pairwise Structure Alignment (в качестве референса была взята структура 1c0t) на сайте PDB алгоритмом TM-align, обычное же выравнивание производилось с помощью программы MUSCLE в Jalview.

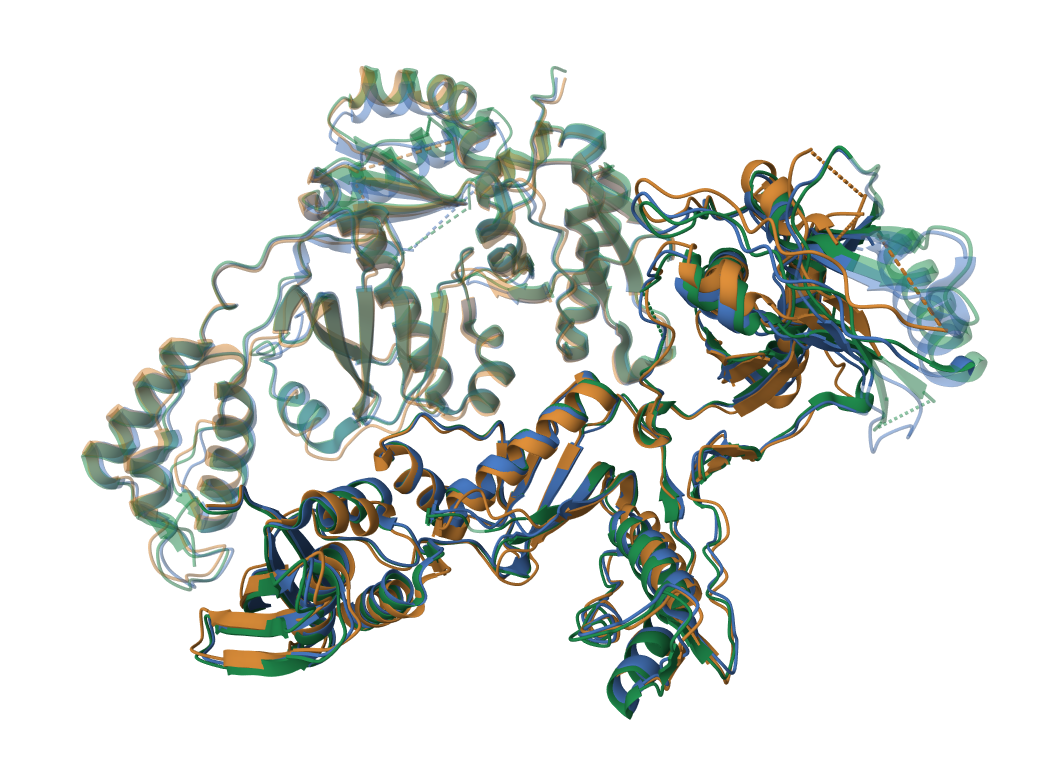
Проект в Jalview

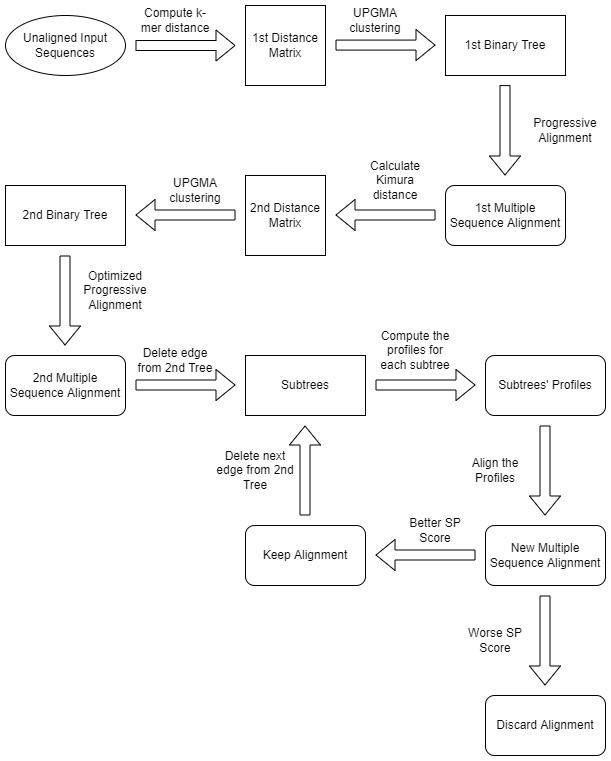
Описание работы программы Muscle

Muscle – алгоритм множественного выравнивания последовательностей (с помощью логарифмического ожидания).
Алгоритм:

Этап 1. Прогрессивный этап. Цель первого этапа — произвести множественное выравнивание, делая упор на скорость, а не на точность.

1. Создание матрицы расстояний, элементами которой являются расстояние k-меров ждя каждой пары последовательностей.
2. На основе матрицы создается бинарное дерево
3. Построение прогрессивного выравнивания в соответствии с порядком ветвления дерева с помощью алгоритма Нидлмана-Вунша: на каждом внутреннем узле строится парное выравнивание двух дочерних профилей, создавая новый профиль, который и назначается этому узлу. То есть происходит многократное выравнивание всех последовательностей.

Этап 2. Улучшенный прогрессивный этап. Повторная оценка дерева с помощью расстояния Кимуры, которое является более точным, чем приблизительная мера расстояний k-меров, но требует выравнивания.

1. Создание матрицы расстояний, элементами которой являются расстояния Кимуры (1983) для каждой пары последовательности
2. На основе матрицы создается бинарное дерево
3. Построение прогрессивного выравнивания (аналогично предыдущему, с помощью алгоритма Нидлмана-Вунша), создается множественное выравнивание. Порядок ветвления поддеревьев в двух этапах разное.

Этап 3. Уточнение.

1. Выбор ребра из дерева этапа 2 (ребро выбирается в порядке приближения к корню)
2. Вычисление профиля множественного выравнивания каждого поддерева, которые получились путем удаления ребра из дерева.
3. Новое множественное выравнивание строится путем выравнивания двух профилей.
4. Если оценка SP (sum of pair) улучшается, то выравнивание сохраняется, а если нет, то сбрасывается. Шаги 1-4 повторяются, пока не будет достигнута сходимость или заданный пользователем предел.