Python для структур и не только
Прикреплю небольшую ссылку на ноутбук по заданиям 1 и 2 Задание 1. Prody и B-факторы часть 1
В этом задании нам было интересно найти остаток с минимальным и максимальным по структуре белка значением В-фактора. Для рассмотрения использовалась структура 3PWL, перед работой в Prody она была предварительно обработана в PyMol (для удобства оставили только молекулу белка). Оказалось, что минимальное среднее по своим атомам значение В-фактора имеет остаток ALA 28 из цепи А (12.394), а максимальное - ARG 41, цепь А (46.408).Далее весь белок был покрашен по В-фактору следующим образом:
> spectrum b, deepteal_white_firebrick, minimum=10, maximum=50
То-есть, более "deepteal"-остатки менее подвижные, а, соответственно, "firebrick" - более подвижные. Увидеть наших героев можно на рисунке 1.
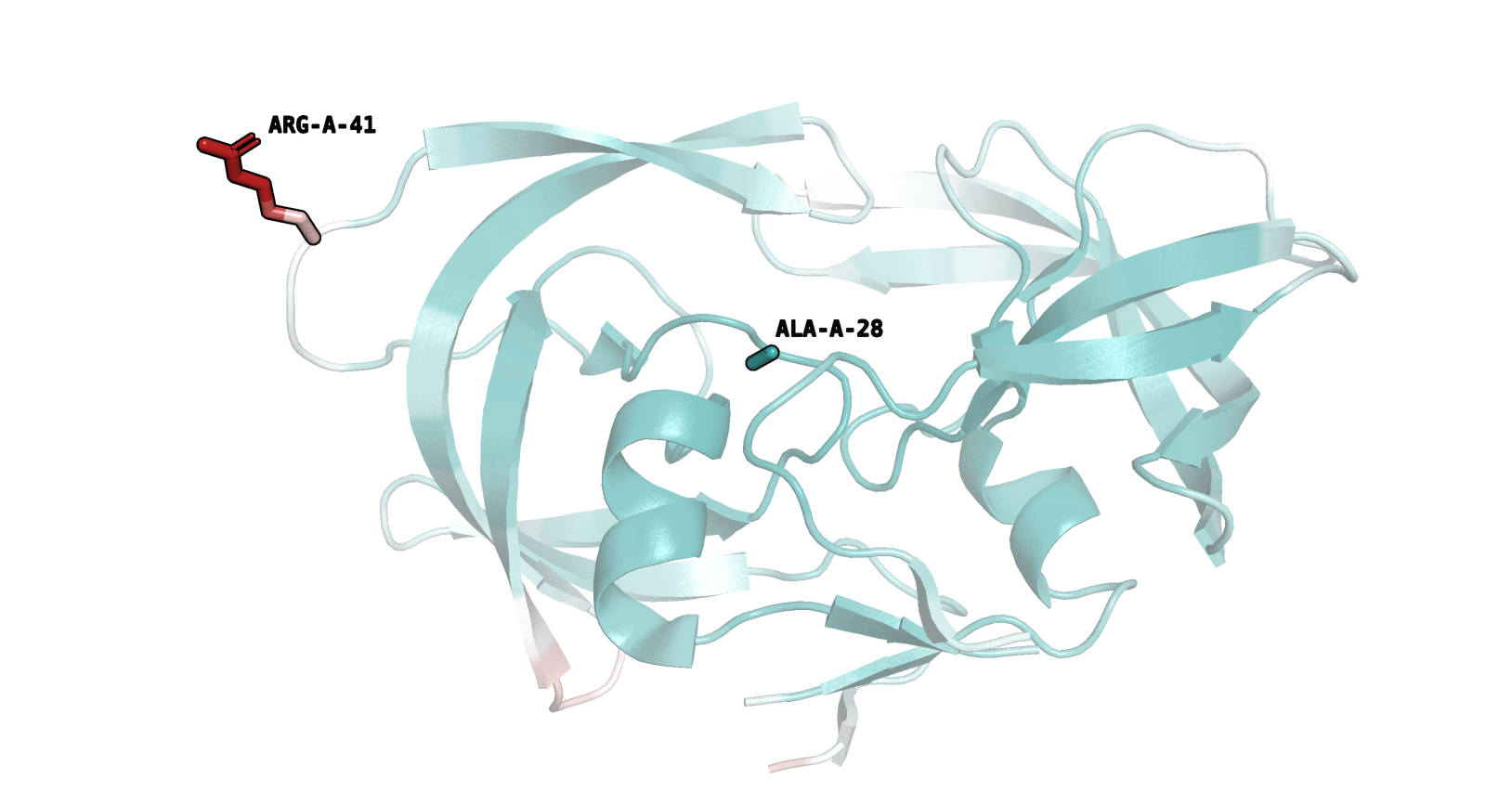
Рассматриваемый нами аргинин расположен на поверхности белковой глобулы и, соответственно, обладает большей подвижностью, нежели аланин, который находится гораздо ближе к центру молекулы (см. рис. 2). В близком окружении аланина - гидрофобный ILE 85 (A), ASP 25 (A) и ASP 29 (A), а также ARG 87 (A), ASP 30 (A).
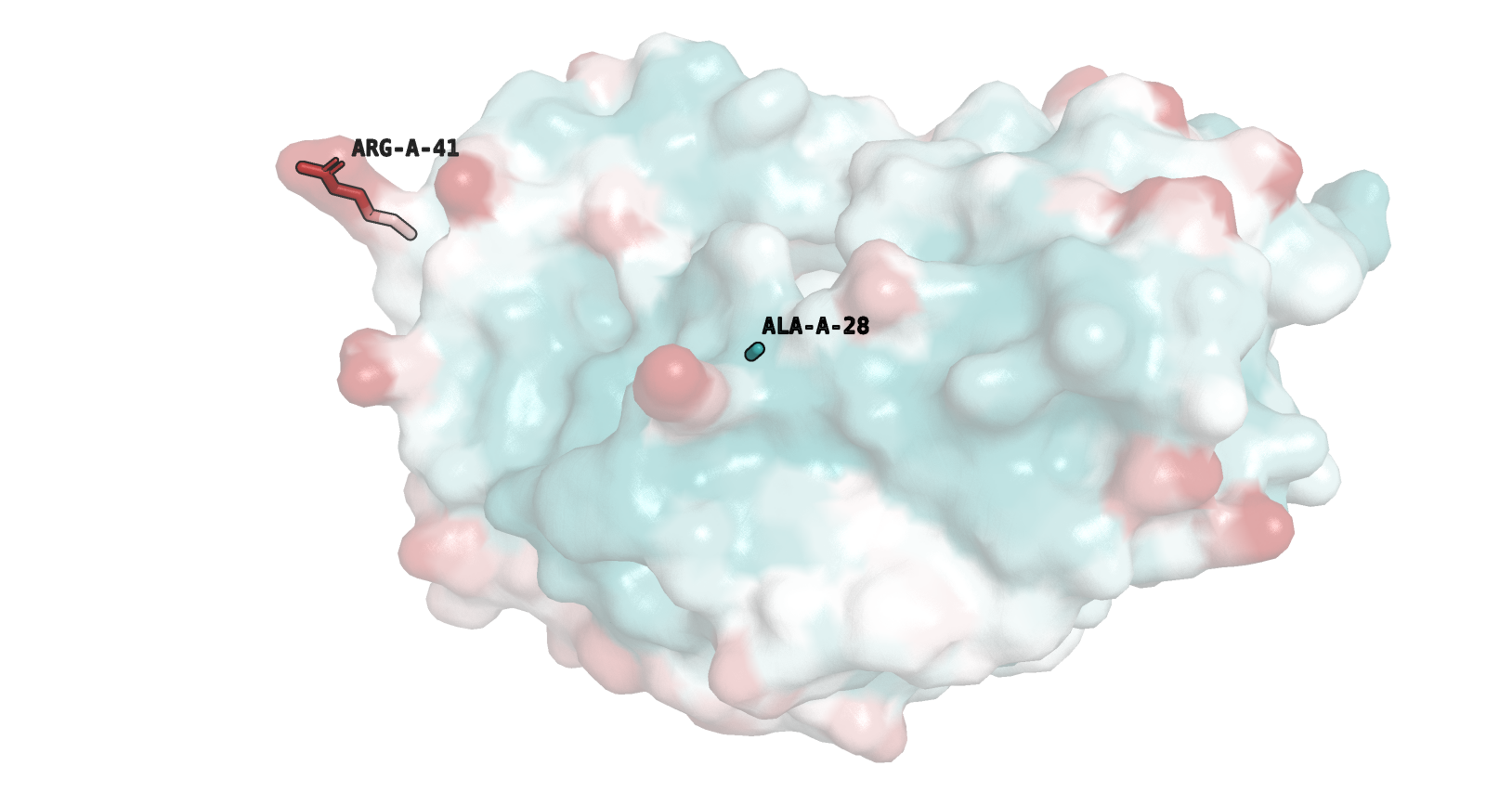
Задание 2. Prody и B-факторы часть 2
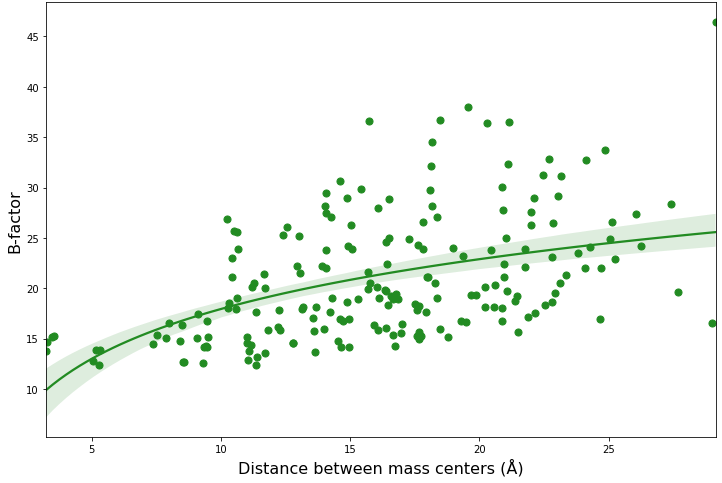
В задании 2 нам было интересно посмотреть, есть ли какая-то зависимость среднего по атомам аминокислотного остатка значения В-фактора и расстояния его центра масс до центра масс всего белка. Прежде всего была предпринята попытка линейной аппроксимации полученных данных, которую можно увидеть на рисунке 3:
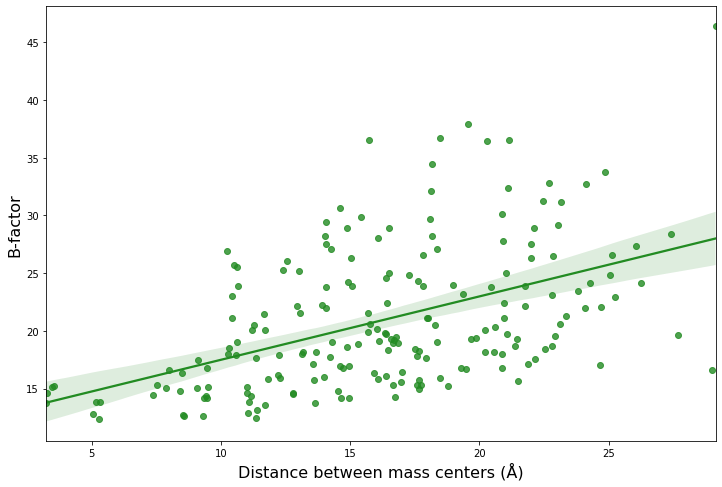
В целом, можно сказать, что наблюдается тренд по увеличению значения В-фактора при удалении центра масс аминокислотного остатка от центра масс белка (остатки, по сути, вынесены на поверхность). Вероятно, распределение будет иметь другой вид для, например, димеров. Также кажется, что линейная аппроксимация не вполне хорошо подходит для наших данных (сложно говорить с полной уверенностью, так как данные обладают достаточно большой дисперсией). Была посчитана корреляция по Пирсону (rho=0.488, p-value=1e(-13)) и по Спирману (rho=0.515, p-value=1e(-15)), на основании этого мы можем предположить, что наблюдаем монотонную (не линейную) зависимость значений В-фактора от расстояния между центрами масс. Попробуем что-нибудь еще. На рисунке 4 можно увидеть попытку полиномиальной аппроксимации (степень=3). Возможно, она выглядит как несколько переобученная модель.
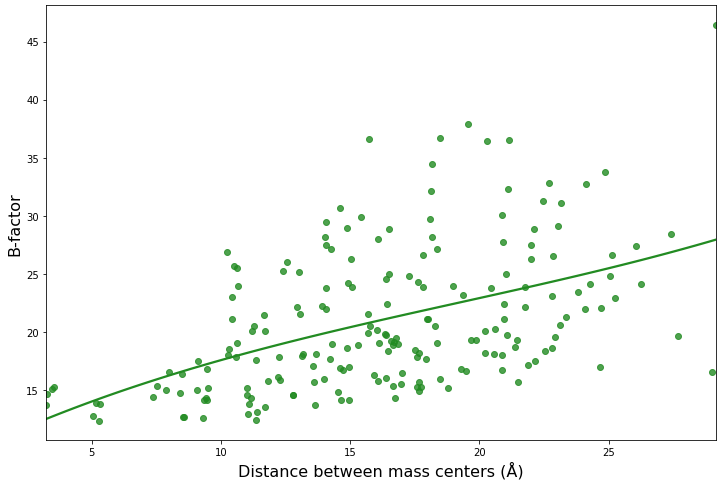
Была произведена и аппроксимация логарифмом (рис. 5), но она кажется наименее удачной из всех трех вариантов (ее вид лучше бы описывал распределение точек, если бы мы отразили ее симметрично относительно оY = 15, например). В целом кажется (если смотреть на полученные графики), что значения В-факторов ограничены снизу величиной, большей 0.
Задание 3. Как работает восстановление функции электронной плотности по экспериментальным данным
Задание функции электронной плотности
Создание функции электронной плотности происходило с помощью скрипта compile-func.py:
> python2.7 compile-func.py -g 16,3,4+12,3,5.5+2,2,6.7+20,4,11+20,4,12.3+3,2,17.3+16,3,18.8+3,2,20.3
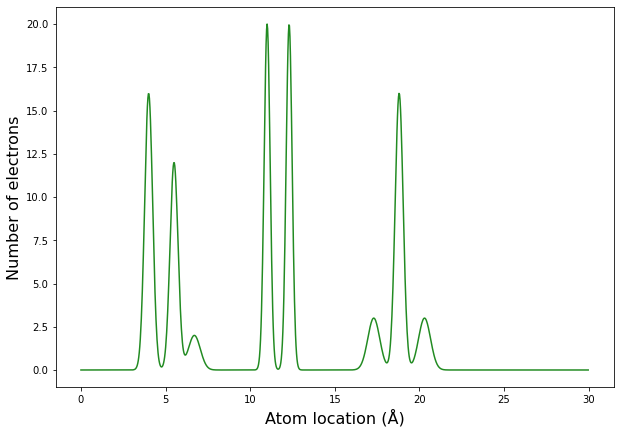
Модель состоит из трех молекул и восьми атомов (рис. 6).
Молекула 1:
атом1: высота пика (число электронов) = 16
атом2: высота пика(число электронов) = 12
атом2: высота пика (число электронов) = 2
расстояние атом1-атом2: 1.5 Å
расстояние атом2-атом3: 1.2 Å
Молекула 2:
атом1: высота пика (число электронов) = 20
атом2: высота пика(число электронов) = 20
расстояние атом1-атом2: 1.3 Å
Молекула 3:
атом1: высота пика (число электронов) = 3
атом2: высота пика (число электронов) = 16
атом3: высота пика (число электронов) = 3
расстояние атом1-атом2: 1.5 Å
расстояние атом2-атом3: 1.5 Å
Расстояние молекула1-молекула2: 4.3 Å
Расстояние молекула2-молекула3: 5.0 Å
Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Функция ЭП была разложена в ряд Фурье программой func2fourier.py, в качестве выдачи мы получили файл func_ft.txt, состоящий из трех колонок:
1) номер гармоники (0..498), всего 499
2) амплитуды гармоник
3) фазы гармоник
Восстановление функции ЭП по амплитудам и фазам (полный набор гармоник, без добавления шума)
Для начала рассмотрим восстановление электронной плотности нашей молекулярной системы по полному набору гармоник.
Набор гармоник ряда Фурье называется полным, если известны все гармоники с номерами 0, 1, 2, ..., n. рассмотрим несколько примеров
восстановления с n=1,5,10..45 (после 5 шаг 5); результаты восстановления ЭП приведены на рисунке 7. Приведем критерии качества, которые мы используем
для оценки качества восстановленной ЭП:
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
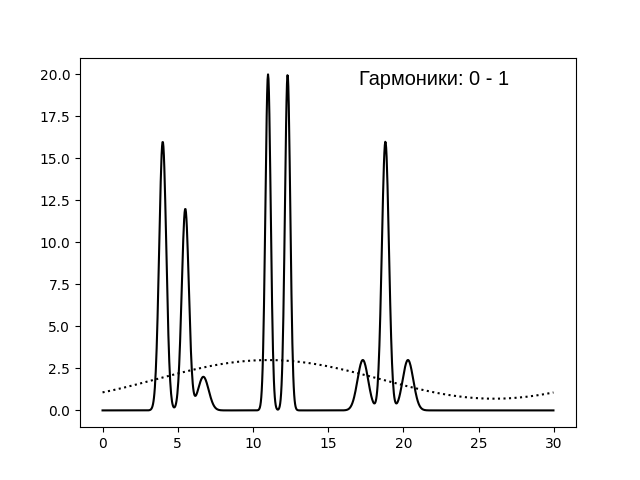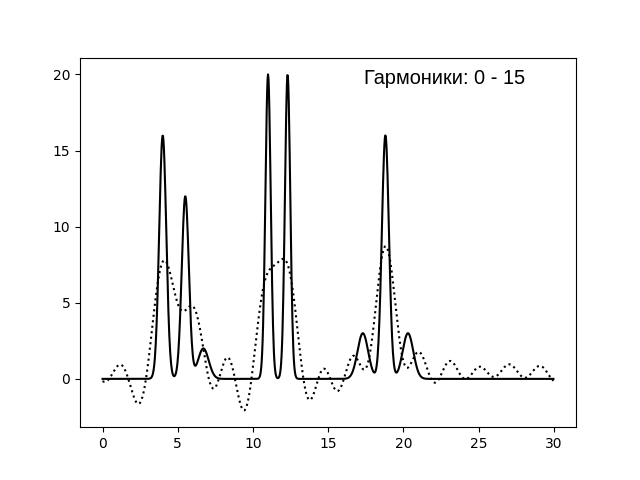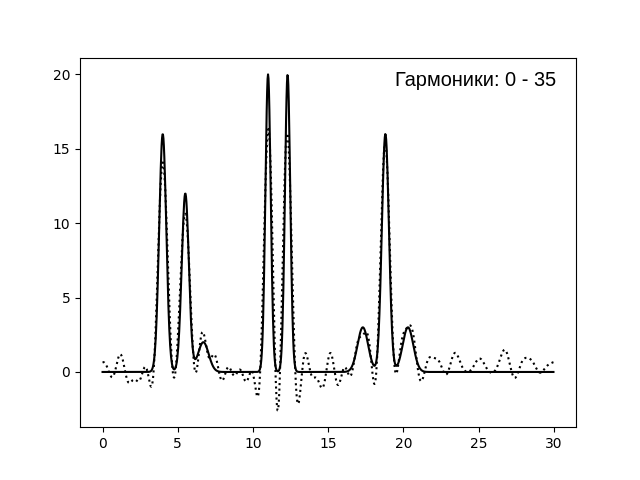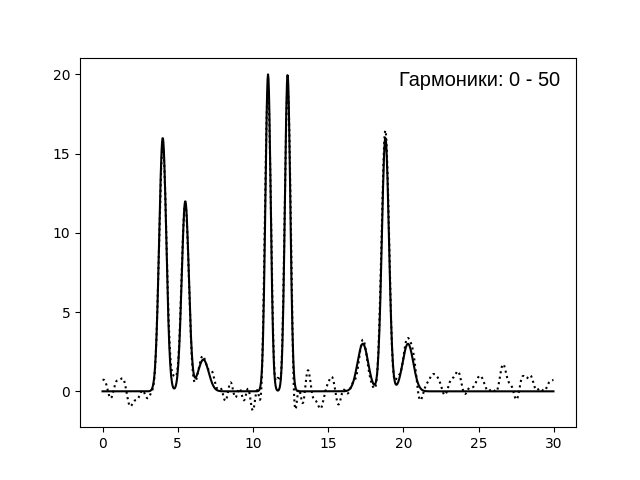
В целом, можно сказать, что при числе гармоник (n) 1..10 качество реконструкции ЭП плохое - при малых значениях
неразличимы не только атомы, но и моолекулы в моделируемой системе. При n=15..25 качество восстановления среднее
(мы можем достаточно точно предположить положение атомов с большим числом электронов ~ амплитудой). В случае с n=30 качество
хорошее (если мы будем знать количество атомов в молекулярной системе, то мы можем предположить, какие пики на графике отображают их
положение). При n=35..45 качество реконструкции - отличное. При используемых нами значениях, n=35 - минимальное количество
гармоник, которое обеспечит отличную реконструкцию электронной плотности. Кажется, правда, что реконструкция при n=40 выглядит лучше (амплитуда шума становится
совсем незначительной. Далее n можно не увеличивать.
Восстановление функции ЭП по амплитудам и фазам (полный набор гармоник, с добавлением шума к амплитуде)
Разложим функцию в ряд Фурье с добавлением к амплитуде шума различного уровня (варьируем % шума от 0 до 50 с шагом 10). Восстанавливать электронную плотность будем по полному набору гармоник с n=35 (как выяснилось ранее, это минимальное их число, необходимое для отличной реконструкции ЭП). Результат можно увидеть на рис. 8.
При увеличении значений параметра F пики атомов (в особенности тех, что имеют в своем составе небольшое число электронов), становятся практически неразличимыми на фоне шума (он приобретает все большую амплитуду). На самом деле, как кажется, в нашей модели увеличение -F до 30% не критично для "хорошего" ЭП. Результаты, полученные при значениях F 40 и 50 можно охарактеризовать как реконструкцию среднего качества.
Восстановление функции ЭП по амплитудам и фазам (полный набор гармоник, с добавлением шума к фазе)
Разложим функцию в ряд Фурье с добавлением к фазе шума различного уровня (варьируем % шума от 0 до 50 с шагом 10). Восстанавливать электронную плотность будем по полному набору гармоник с n=35 (как выяснилось ранее, это минимальное их число, необходимое для отличной реконструкции ЭП). Полученные результаты приведены далее:
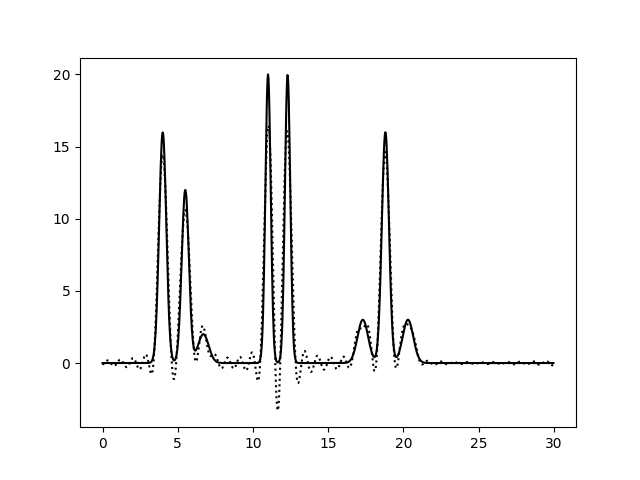
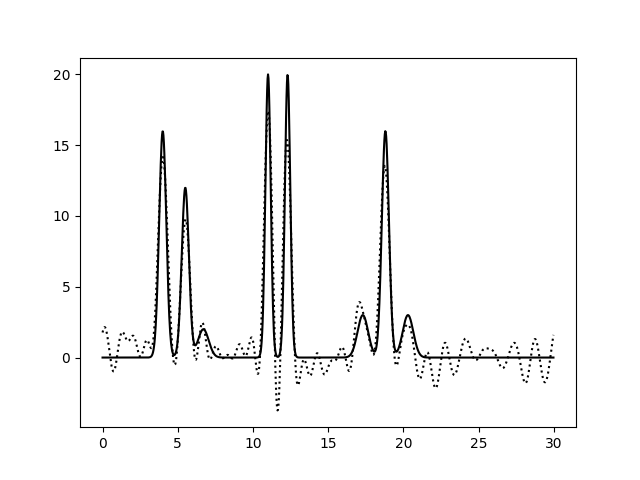
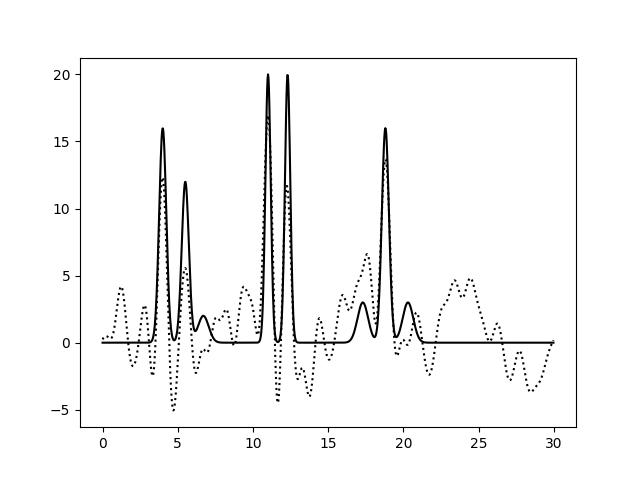
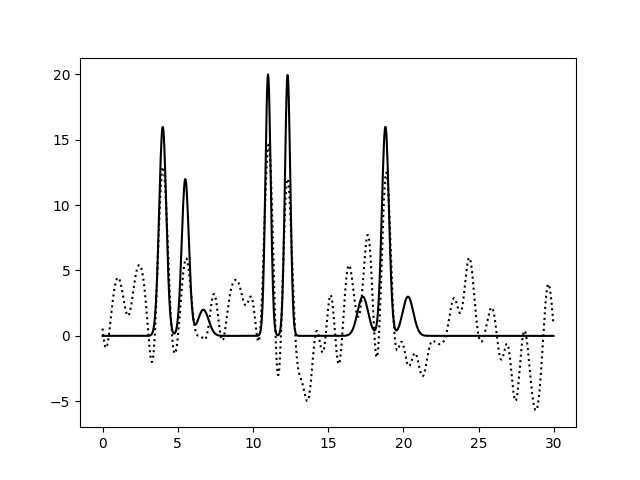
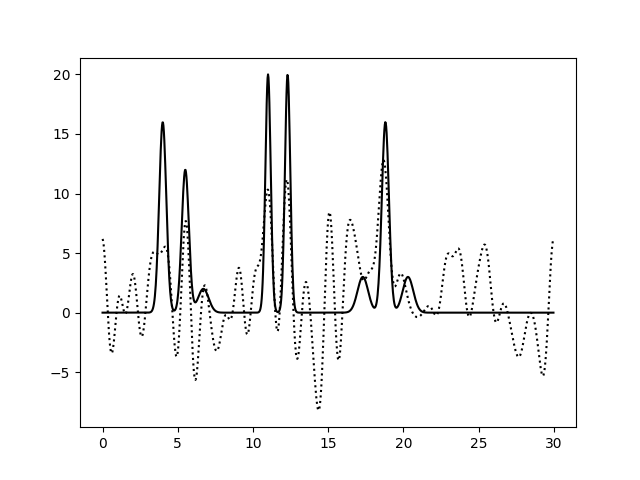
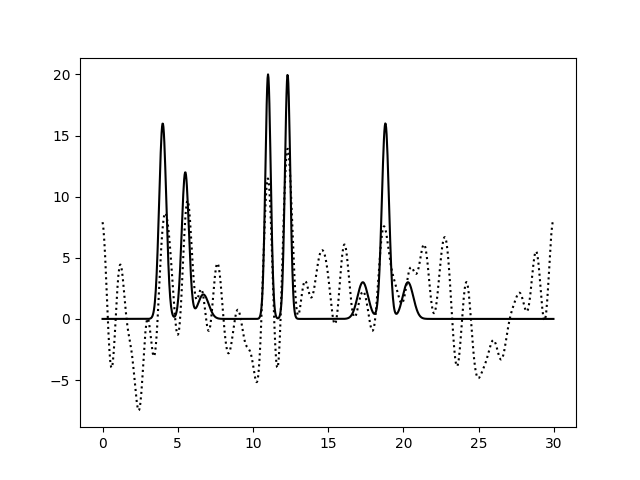
Добавление шума к фазе значительно снижает качество восстановленной электронной плотности. При P = 0 качество реконструкции
отличное, при P=10 его можно охарактеризовать как "хорошее", в связи с тем, что происходит небольшой сдвиг положения
пиков. При P=20, 30 качество среднее, так как мы можем некоторым образом
определить положение только 1, 3, 5, 7 атомов. Остальные пики претерпевают значительное смещение и/или уменьшение амплитуды.
>=40% уровень шума в фазе делает реконструкцию плохой - мы не можем определить положение атомов.
В целом, можно сказать, что уровень "фазового шума" более критичен для качества реконструкции электронной плотности, нежели шум в амплитуде.
Неполный набор гармоник. Удаление начальных гармоник
По идее, чем больше номер гармоники, тем она "лучше" (лучше ее разрешение). Поэтому, мы предполагаем, что удаление первых гармоник не повлечет за собой фатальных для восстановления электронной плотности последствий. Попробуем удалить первую гармонику под номером 0 и произвести реконструкцию ЭП по 1..35 гармоникам. Результат приведен на рисунке 15:
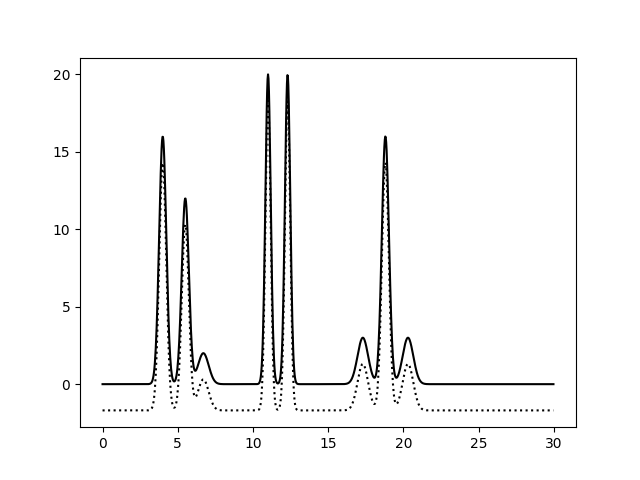
Теперь посмотрим, как на качестве восстановления электронной плотности скажется удаление гармоник из разных частей набора.
Предполагаем, что произведенная реконструкция будет тем хуже, чем больше номера удаленных гармоник. Так как эффект удаления гармоник
из начала набора мы уже наблюдали ранее, рассмотрим теперь середину и ~ вторую треть набора
Неполный набор гармоник. Удаление 14, 15, 16 гармоник
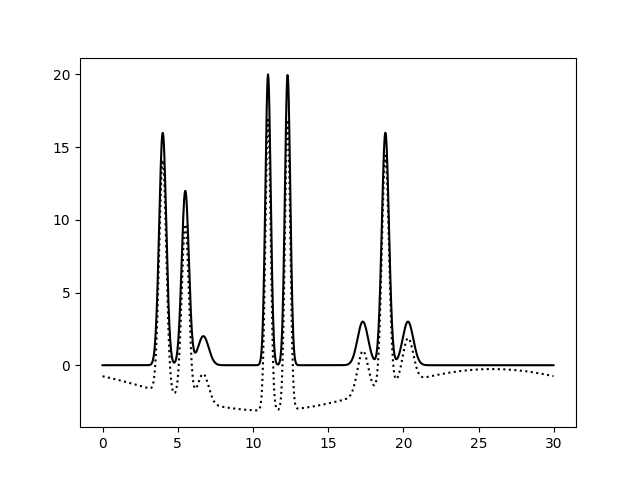
Посмотрим на функцию, полученную в результате реконструкции по неполному набору гармоник 0..13, 17..35:
Качество восстановленной электронной плотности ухудшилось (мы удалили гармоники с достаточно хорошим разрешением) и стало средним (более-менее достоверно мы можем определить положение только 1, 2, 4, 5, 7 атомов). В качестве разрешения неполного набора гармоник возьмем разрешение 21 гармоники.
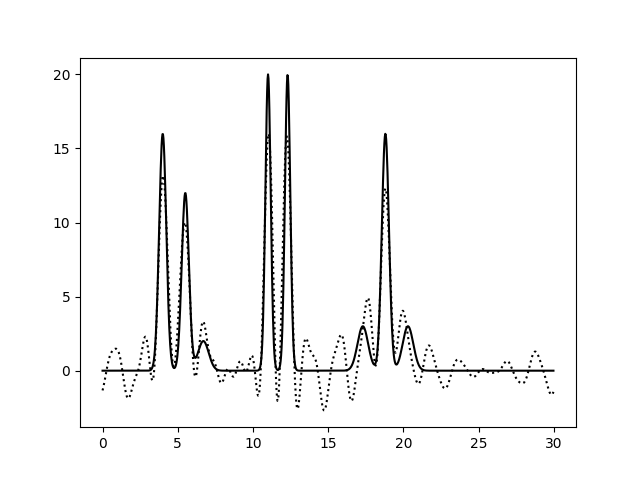
Неполный набор гармоник. Удаление 29, 30, 31 гармоник
Восстановление ЭП было произведено по неполному набору гармоник 0-28 и 32-35 По нашей модели получается, что в данном случае качество восстановленной электронной плотности снижается, но незначительно (качество реконструкции можно даже назвать отличным) - не вполне ожидаемый результат. Стоит упомянуть, что пик 3 атома практически сравним по амплитуде с шумом.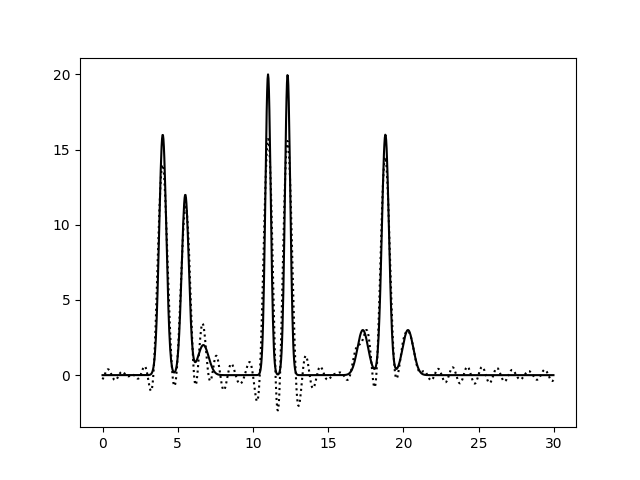
Добавление 45 гармоники
Чтобы проверить влияние добавления "старшей" по номеру гармоники в набор, возьмем для сравнения уже рассмторенный нами неполный набор гармоник 0..14, 14..35 и добавим в него 45 гармонику (35 + 10, согласно заданию). Результат представлен на рисунке 19.
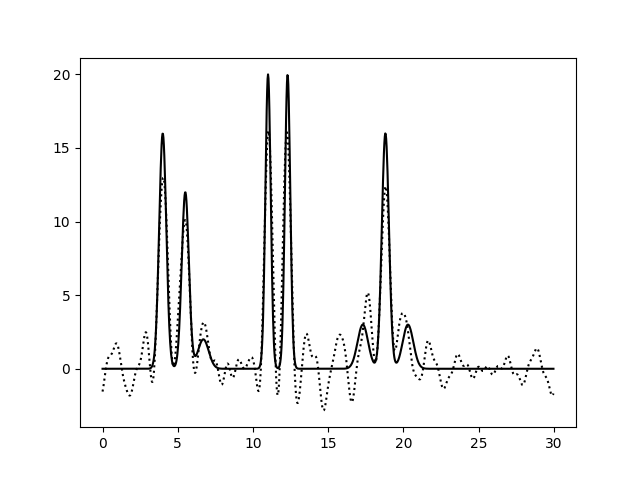
Добавление 45 гармоники
Добавление 45 гармоники не повлекло за собой улучшения восстановления ЭП. Почему так произошло? Ранее мы выяснили, что минимальное количество гармоник, достаточное для получения электронной плотности отличного качества равно 35. Поэтому, вероятно, добавление старших гармоник - это некоторое ненужное уточнение минимального набора. В данном случае больший вклад вносит потеря 14-16 гармоник. В качестве разрешения неполного набора гармоник возьмем разрешение 21 гармоники (электронная плотность недостаточно высокого качества, поэтому мы не будем брать разрешение гармоник с наибольшим намером в качестве разрешения рассматриваемого неполного набора).
Ссылка на таблицу