Восстановление электронной плотности

Создание модельной функции ЭП в одномерной элементарной ячейке

Командой "python compile-func.py -g 2,3.5,5+16,3,6+13,3,7.2+16,3,8.5+2,3.5,11.7+16,3,12.8+2,3.5,13.9 -o func_1.txt" была получена функция g, которая должна отобразить идеальную электронную плотность двух молекул из четырех и трех атомов. Текстовый файл можно скачать по ссылке: func_1.txt.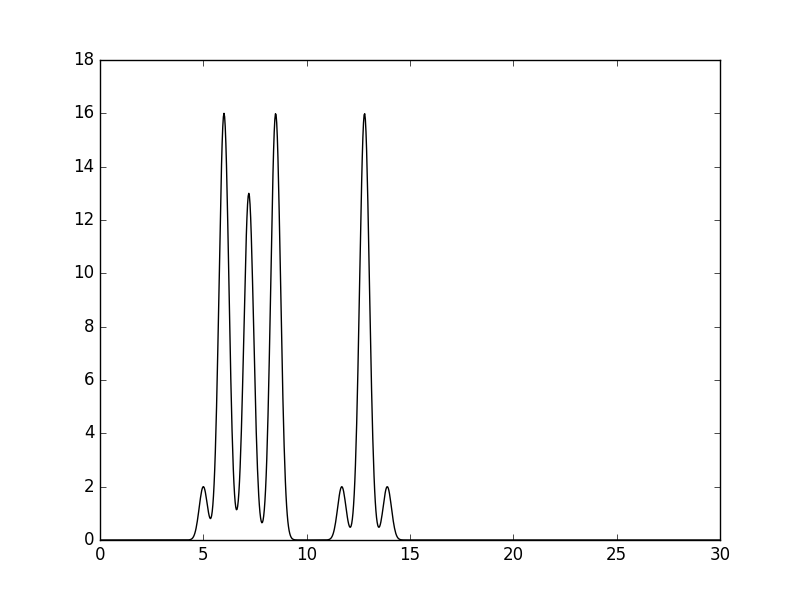

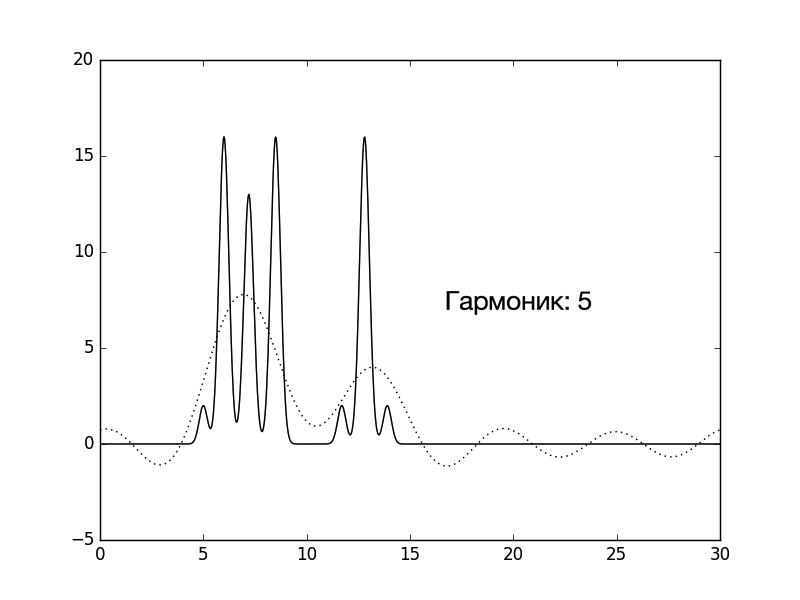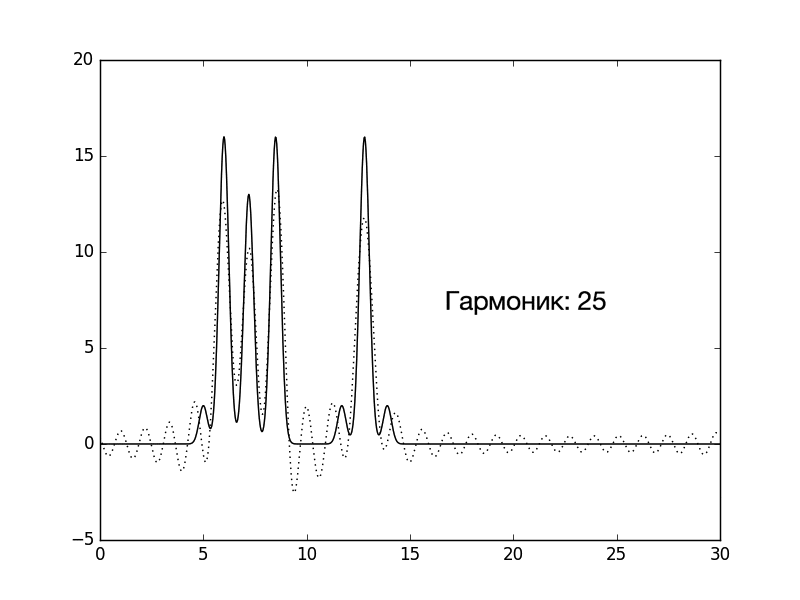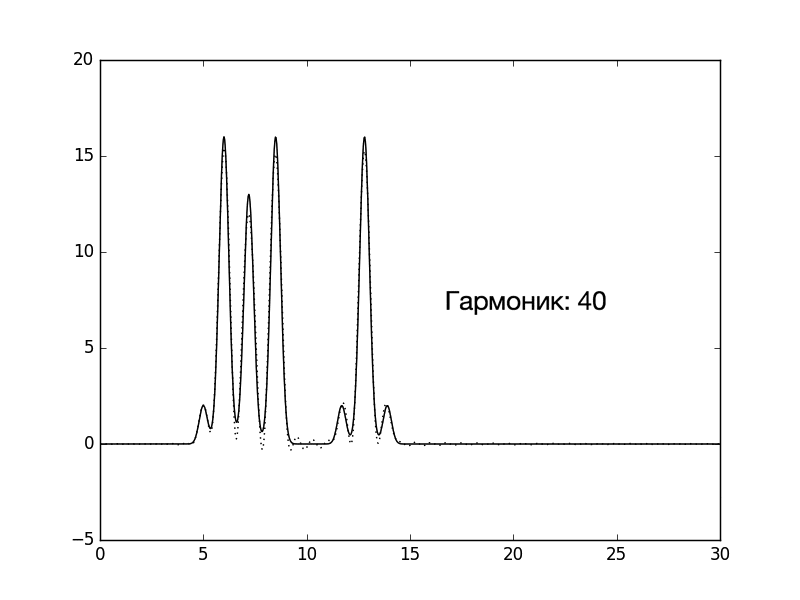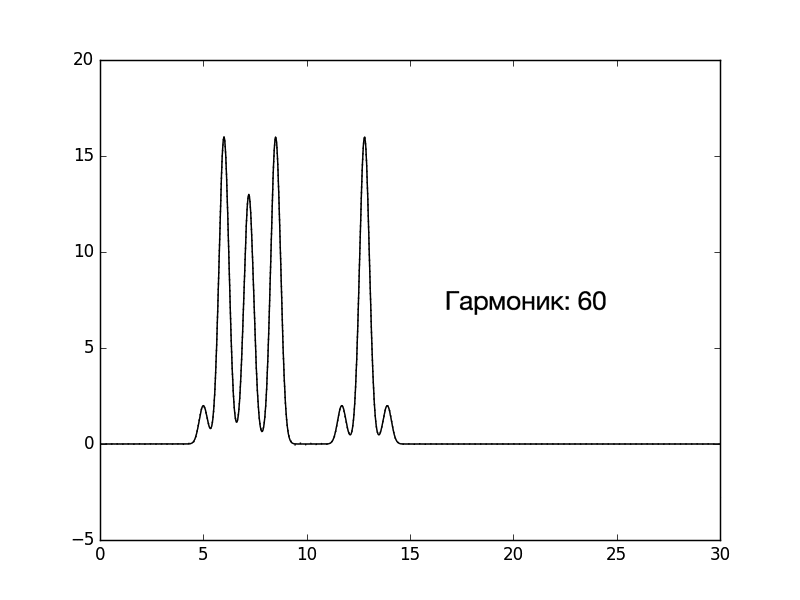
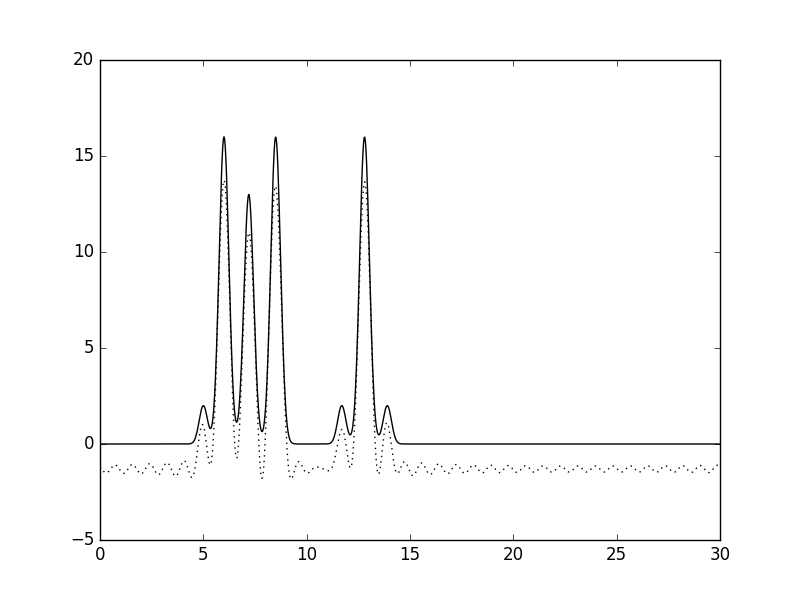
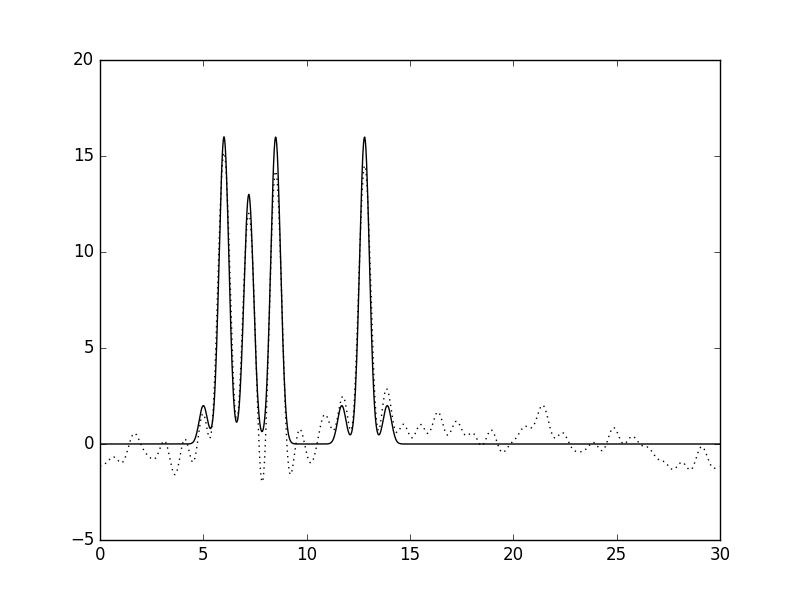
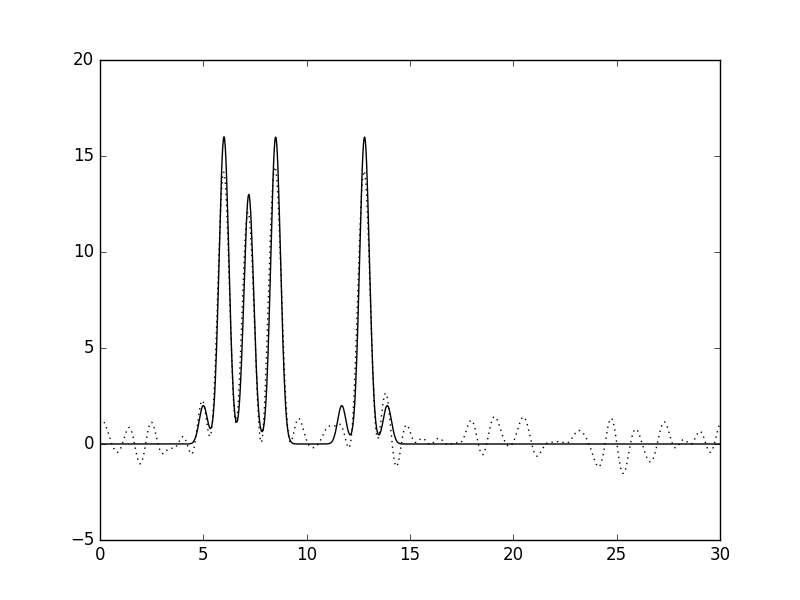
Рисунок 1. Изображение функции Гаусса, использованной в качестве одномерной модели расположения двух молекул.

Расчет параметров сигнала, моделирующих экспериментальные данные: амплитуды и фазы

С помощью скрипта func2fourier.py были получены файлы:

1) Для идеального эксперимента.

2) С учетом 10% гауссова шума к амплитудам.

3) С учетом 10% гауссова шума к фазам.

4) С учетом 10% гауссова шума и к амплитудами, и к фазам.

Затем, с помощью скрипта fourier-filter.py были отобраны гармоники из файла для идеального эксперимента:

1.1) 0-5*i, где i от 1 до 12.

1.2) 1-35

1.3) 0-35,45

1.4) 1-14,18-35

Восстановление функции ЭП по модельным данным

Для начала были проанализированы функции ЭП с гармониками 0-5*i (1.1). На рисунке 2 можно посмотреть на то, как увеличение количества гармоник улучшает качество восстановления. Уже при гармониках от 0 до 30 функция легко угадывается, а при 0-35 – почти идеально. Поэтому, собственно говоря, для экспериментов 1.2-1.4 и 2-4 предел для гармоник равен 35.

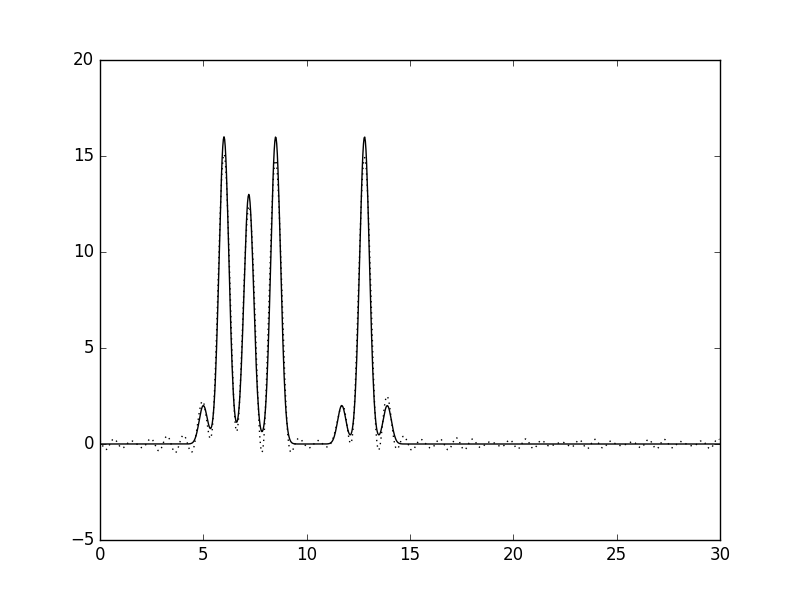
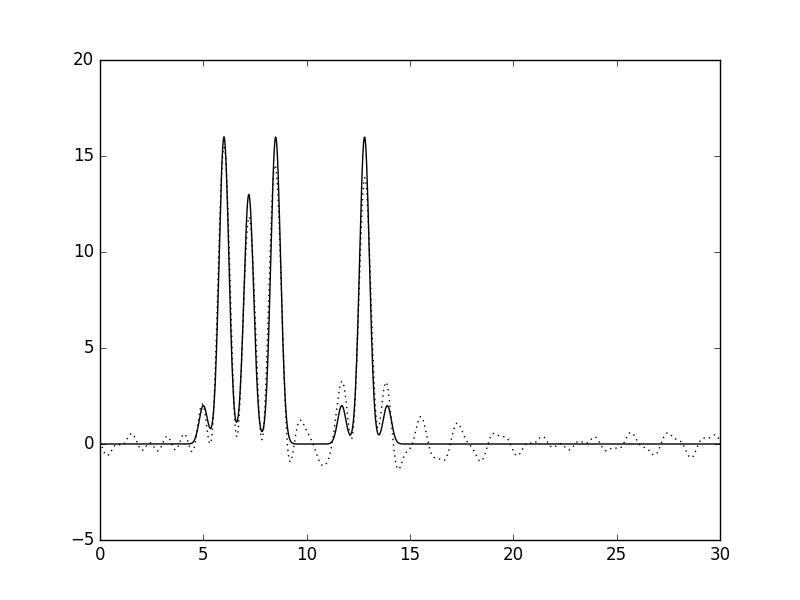
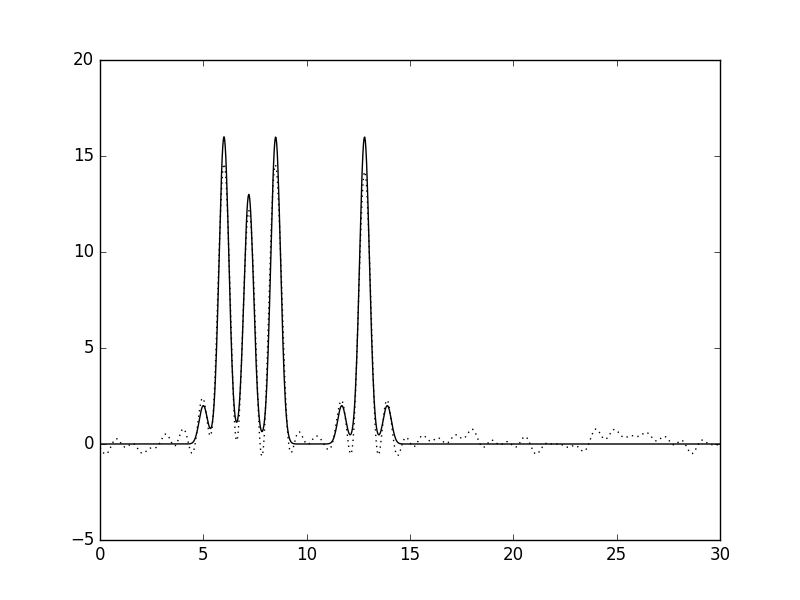
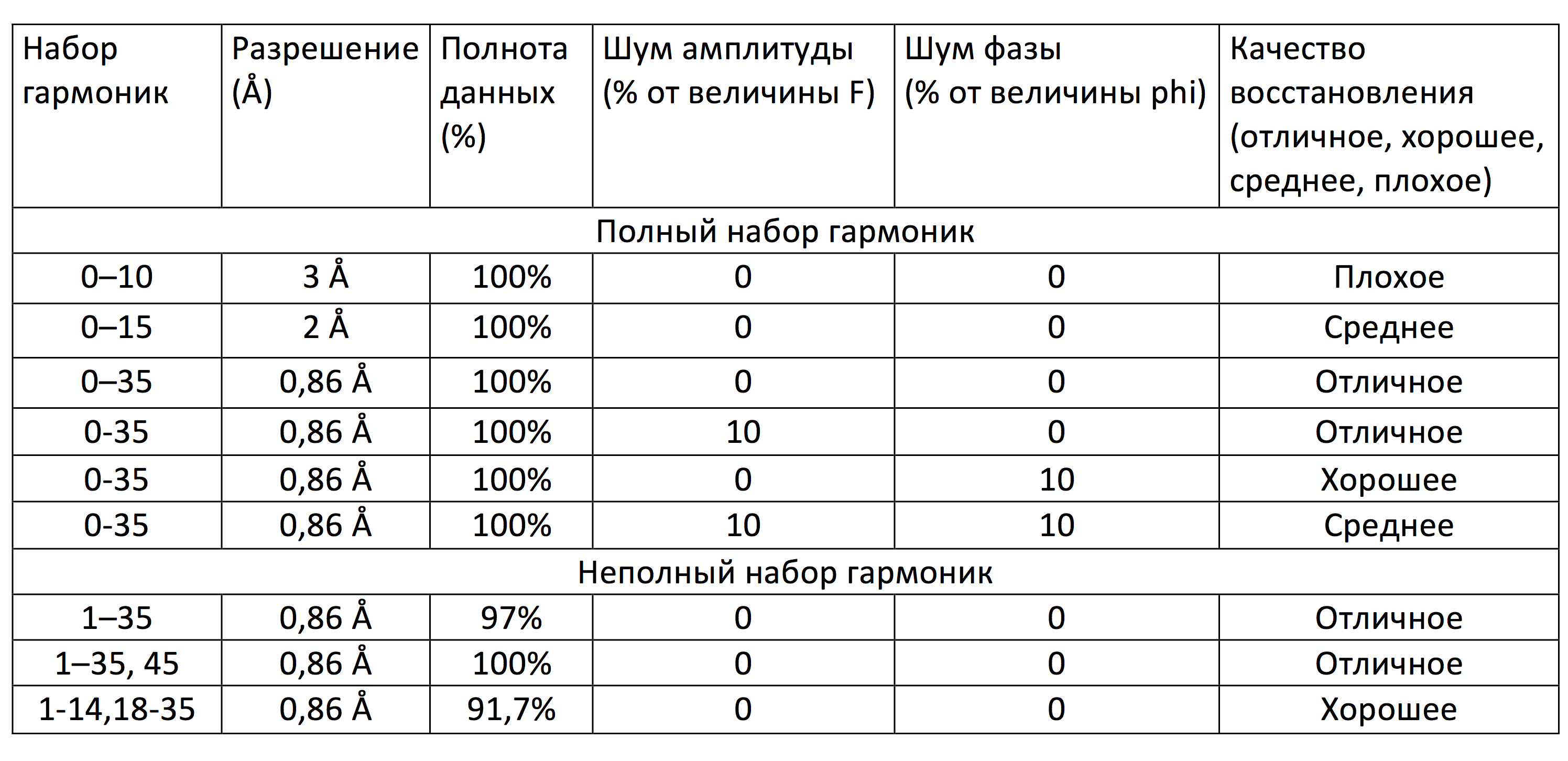
Рисунок 2. Изменение качества восстановления функции ЭП в зависимости от количества взятых гармоник.

Далее были проанализированы функции ЭП 1.2-1.4. Результаты можно видеть на рисунках 3-5.

Рисунки 3-5 (кликабельны). Восстановление функции ЭП при изменениях количества гармоник. Первый рисунок – удалена нулевая гармоника, второй рисунок – добавлена 45-я гармоника, третий рисунок – удалены 15-17 гармоники.

Потом был проведен анализ гармоник с учетом гауссова шума (6-8)

Рисунки 6-8 (кликабельны). Восстановление функции ЭП с учетом гауссова шума. Первый рисунок – 10% шума к амплитудам, второй рисунок – 10% шума к фазам, третий рисунок – 10% шума и к амплитудам, и к фазам.

Результаты анализа описаны в таблице 1 (кликабельна):

Таблица 1, оценка результатов