Разложение функции ЭП в ряд Фурье

Задание функции электронной плотности

Функия ЭП была смоделирована на отрезке [0,30] для двух молекул из двух и трех атомов на расстоянии примерно 4А. Для этого с помощью скрипта compile-func.py. Комманда с параметрами имела вид:

python compile-func.py -g 25,3.1,7+21,3.0,8.3+11,3.0,12.5+10,3.2,14+27,3.5,15.1 -o func.txt

В каждом слагаемом внутри параметра -g первое число - величина пика, второе число - ширина пика, третье число - точка максисума пика.

В результате получен файл func.txt со значениями функции ЭП, на рисунке 1 построен ее график.

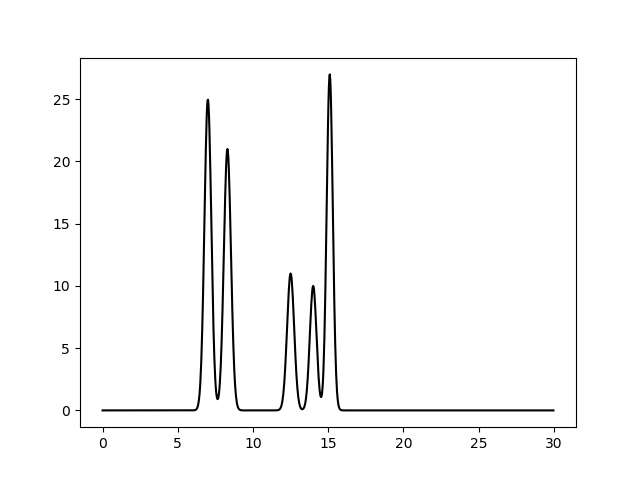
Рис. 1. Одномерная функция ЭП для двухатомной и трехатомной молекул

Расчет амплитуд и фаз сигналов, моделирующих эксприментальные данные

Пороизведен расчет коэффициентов Фурье с помощью скрипта func2fourier.py:

python func2fourier.py -i func.txt -o fouriercoef.txt

Итог - fouriercoef.txt, где в трех столбцах для каждой из 498 гармоник приведены ее номер no, амплитуда P и фаза phi. Такие гармоники необходимы для полного восстановления исходной функции ЭП.

Далее требовалось подобрать такое минимальное количество гармоник, по которому можно точно (по оценке графика на глаз) восстановить исходную функцию. Для этого из исходного файла с помощью скрипта fourier-filter.py из полученного файла fouriercoef.txt отфильтровывалось определенное число k гармоник:

python fourier-filter.py -i fouriercoef.txt -r 0-k -o func_ft_filtered.txt

По отобранным гармоникам функция восстанавливалась при помощи скрипта fourier2func.py:

python fourier2func.py -f func.txt - i func_ft_filtered.txt -o func_k.txt

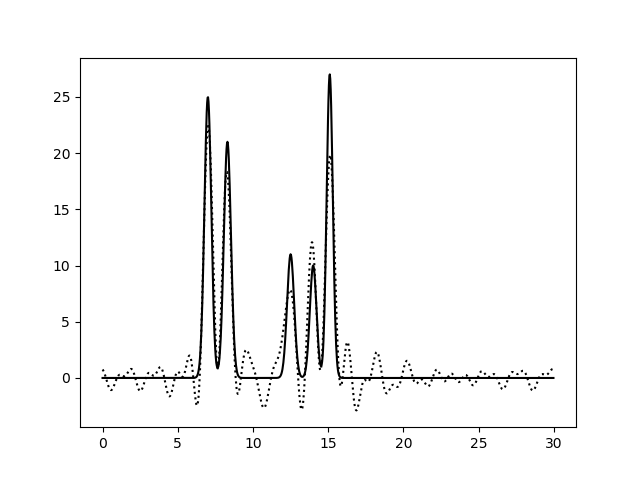
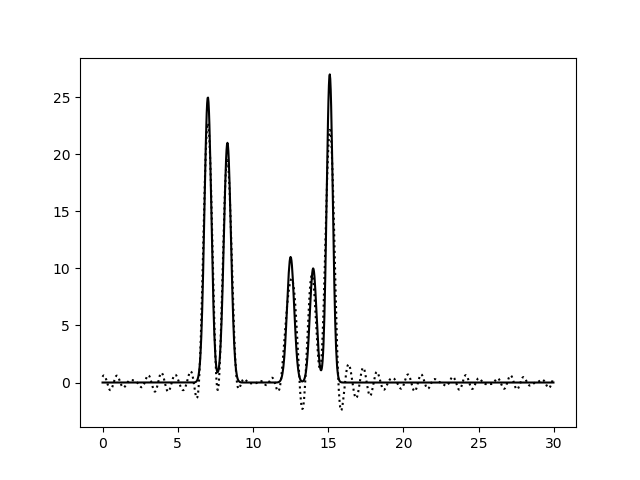
Результаты этих операций на рисунках 2-5. Использовались значения k = 10, 15, 25, 30.

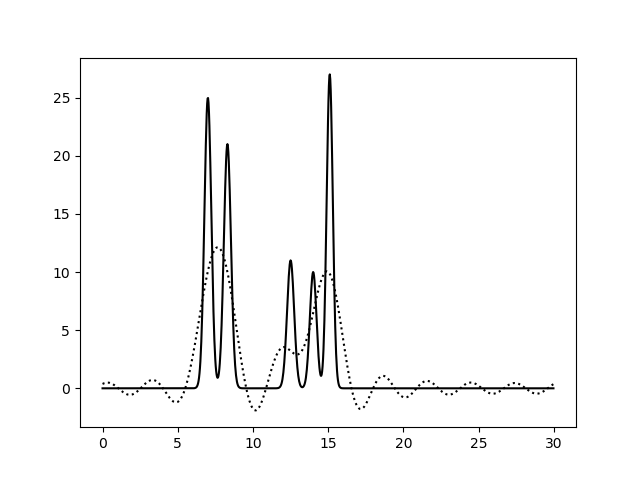
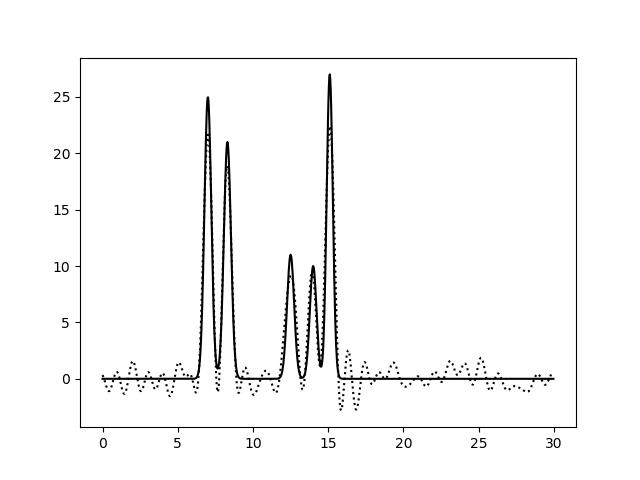
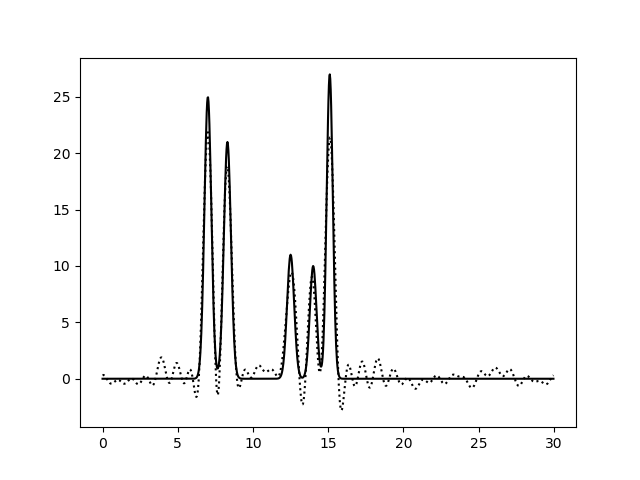
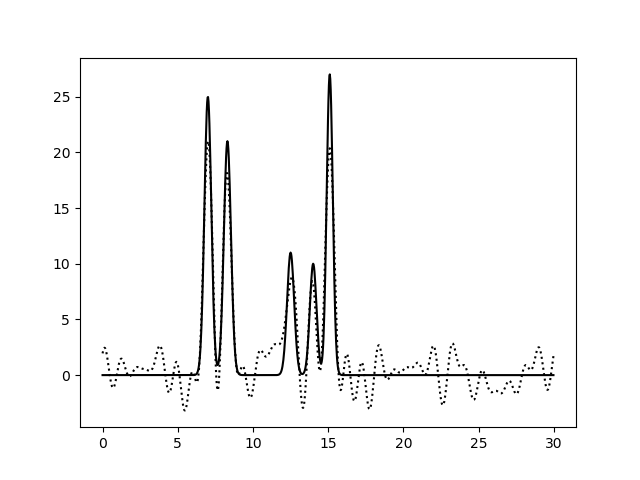
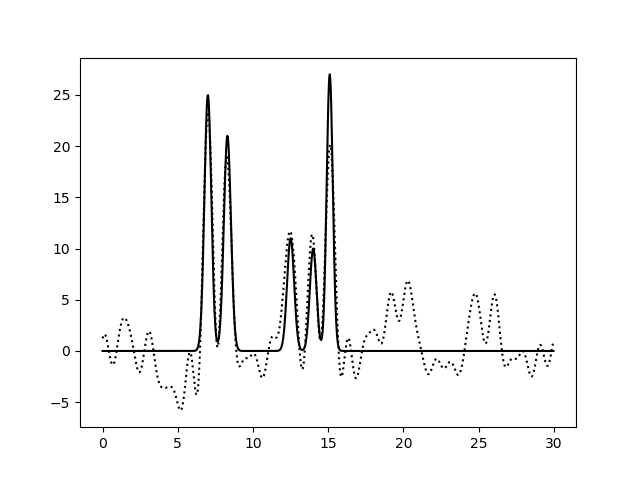
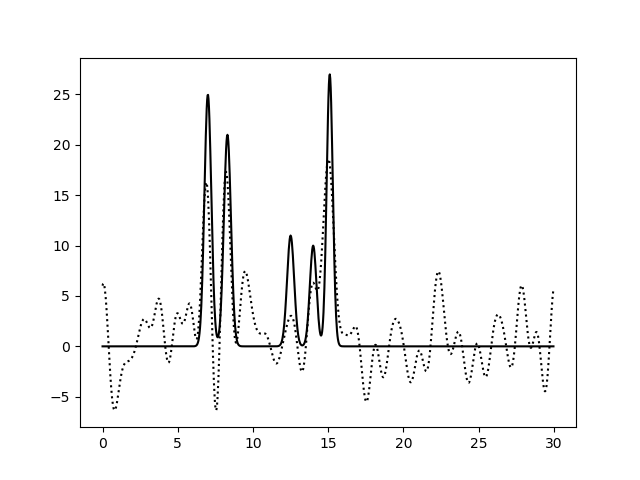
Рис. 2. Восстановление функции по первым 10 гармоникам

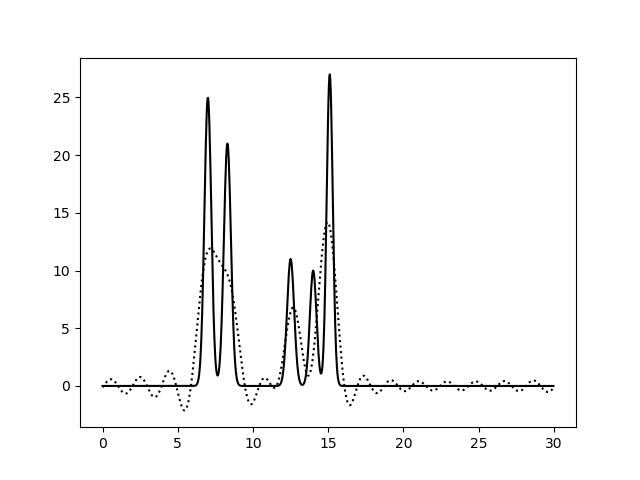
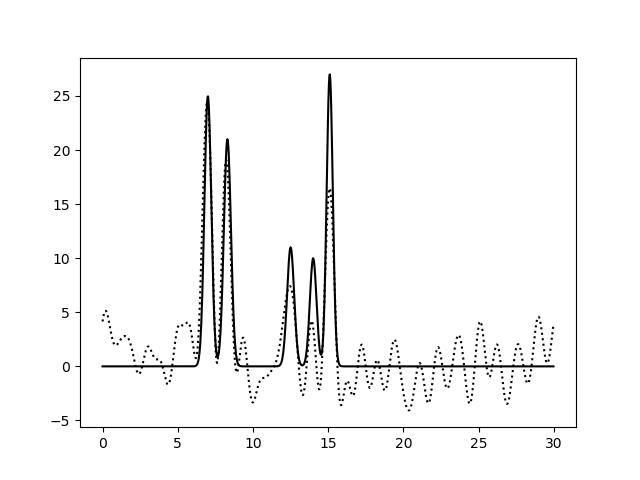
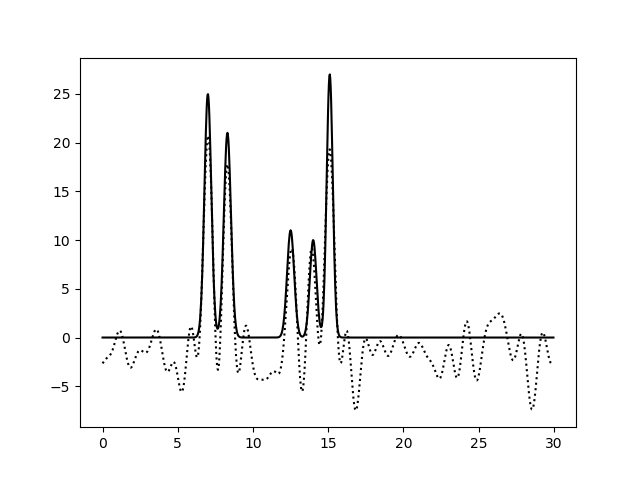
Рис. 3. Восстановление функции по первым 15 гармоникам

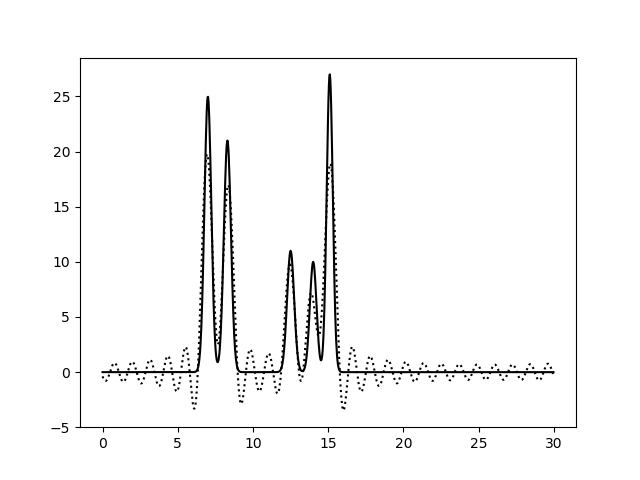
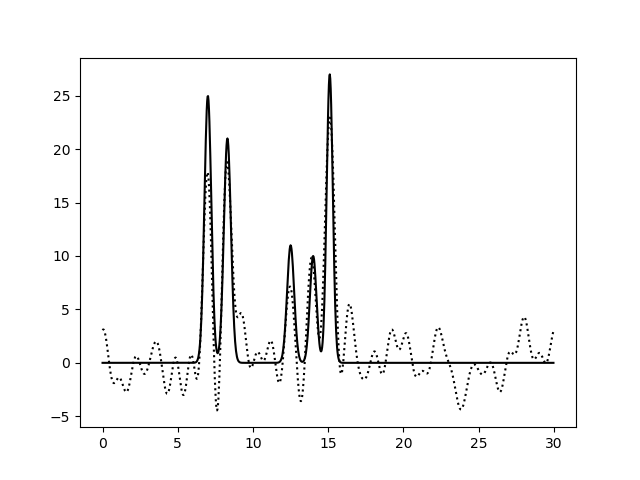
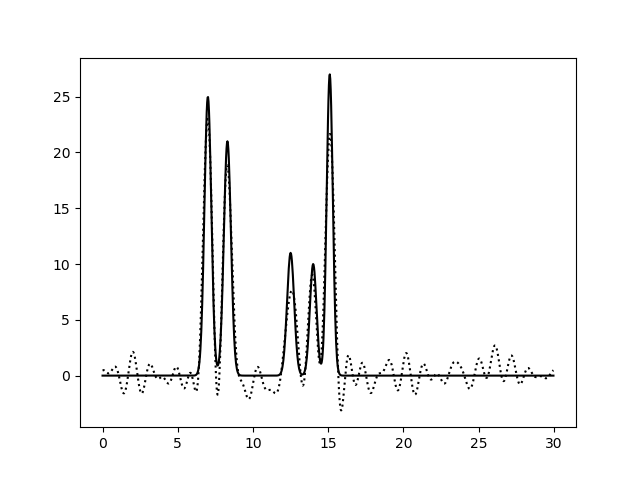
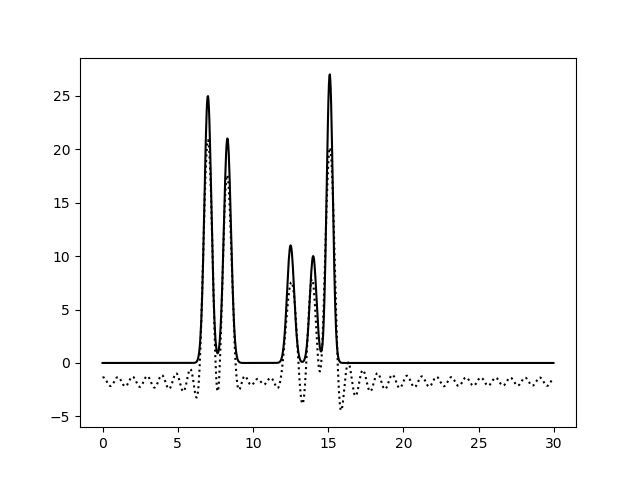
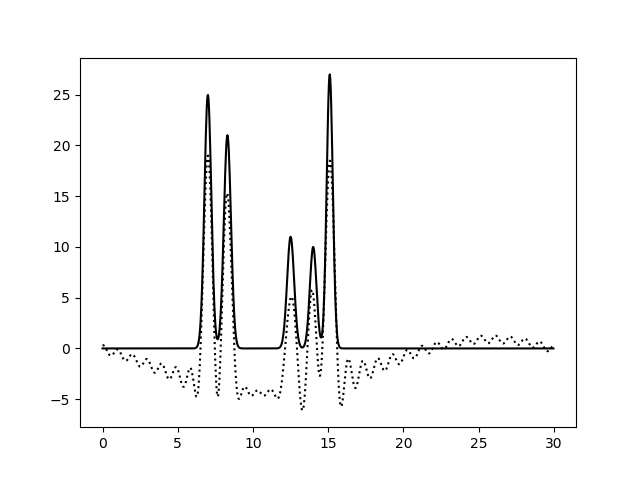
Рис. 4. Восстановление функции по первым 25 гармоникам

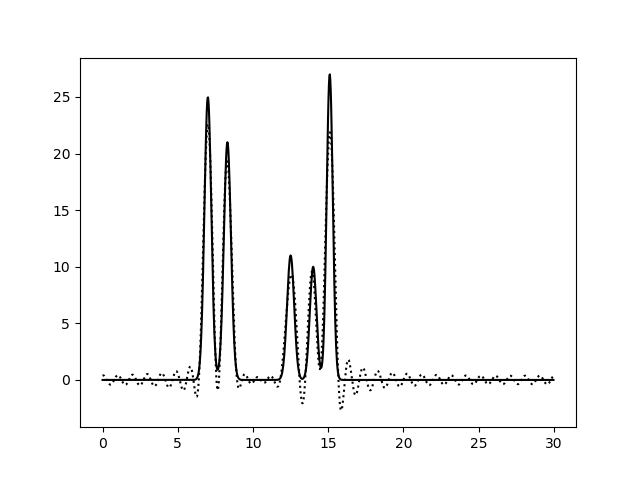
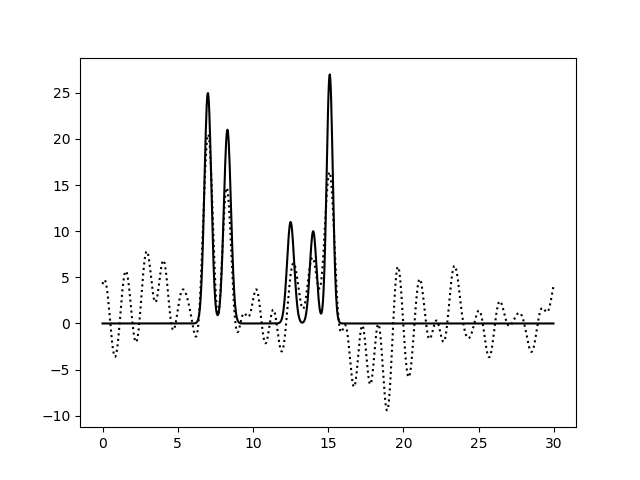
Рис. 5. Восстановление функции по первым 30 гармоникам

Из рисунков 2-5 видно, что по 10 и 15 гармоникам неверно определяется даже число пиков, по 25 гармоникам функция восстанавливается хорошо (если бы в молекуле были атомы с малой величиной пиков, их можно было бы спутать с шумом), по 30 гармоникам функция восстанавлвается отлично - положения всех атомов очевидны. То есть по первым 25 гармоникам уже можно определить число и положение атомов в соединении. Восстановление по 30 гармоникам можно считать отличным, далее будем использовать его как отлично восстановление с минимальным числом гармоник.

Влияние шумов в параметрах гармоники на восстановление функции ЭП

Гауссовский шум вносился в набор из 30 гармоник в амплитуды (M%), в фазы (N%), в амплитуды и фазы вместе с помощью команд:

python func2fourier.py -F M -P N -i func.txt -o file_noise.txt

python fourier-filter.py -r 0-30 -i file_noise.txt -o file_noise.txt

python fourier2func.py -f func.txt -i file_noise.txt -o fpXY.txt

Результаты на рисунках 6-17.

Рис. 6. Шум 10%

Рис. 7. Шум 20%

Рис. 8. Шум 30%

Рис. 9. Шум 50%

Выше зашумление данных только по фазам

Рис. 10. Шум 10%

Рис. 11. Шум 20%

Рис. 12. Шум 30%

Рис. 13. Шум 50%

Выше зашумление данных только по амплитудам

Рис. 14. Шум 10% по фазам, 50% по амплитудам

Рис. 15. Шум 10% по амплитудам, 50% по фазам

Выше зашумление данных по амплитудам и фазам

Можно видеть, что добавление шума к фазе сильнее ухудшает качество восстановления, чем добавление шума к амплитуде.

Восстановление функции электронной плотности по неполным наборам гармоник

При расшифровке структур в реальной жизни часто приходится расшифровывать структуры по неполным наборам гармоник. Аналогично с получением файлов с первыми гармониками получили разнообразные неполные наборы, представлены на рисунках 16-19.

Рис. 16. Восстановление по 1-30 гармоникам

Рис. 17. Восстановление по 2-30 гармоникам

Рис. 18. Восстановление по 0-12,16-30 гармоникам

Рис. 19. Восстановление по 0-30,40 рармоникам

При удалении нулевой гармоники функция не меняет вид, но смещается вниз по оси ординат (понятный эффект, если знать, что нулевая гармоника - константа). При удалении нулевой и первой гармоник на графике появилась "яма", он стал похож на синусоиду. Если построить график первой гармоники, то видно, что это синусоида с максимумом в области "центра" нашего пятиатомного соединения, так что провал при ее удалении понятен. Удаление гармоник из середины набора ухудшило качество восстановления, а добавление одной гармоники никак на качество не повлияло (поскольку высокочастотные гармоники имеют пренебрежимо малую амплитуду).

Сравнение восстановленных функций с исходной

В таблице 1 собрана информация о всех представленных графиках. качество восстановления оценивалось по следующей шкале:

Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции
Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых, хотя на восстановленной функции максимумы от атомов не отличимы от шума
Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"

Таблица 1. Восстановление функции по коэффициентам ряда Фурье

Набор гармоник	Разрешение (Å)	Полнота данных (%)	Шум амплитуды (%F)	Шум фазы (%phi)	Качество восстановления	Комментарии
Полный набор гармоник
0-10	3	100	0	0	плохое
0-15	2	100	0	0	среднее
0-25	1.2	100	0	0	хорошее
0-30	1	100	0	0	отличное
0-30	1	100	0	10	хорошее
0-30	1	100	0	20	среднее
0-30	1	100	0	30	плохое
0-30	1	100	0	50	плохое
0-30	1	100	10	0	отличное
0-30	1	100	20	0	хорошее
0-30	1	100	30	0	среднее
0-30	1	100	50	0	плохое
0-30	1	100	50	10	среднее
0-30	1	100	10	50	плохое
Неполный набор гармоник
1-30	1	96.7	0	0	отличное	функция "съехала" вниз
2-30	1	93.5	0	0	отличное	прогиб вниз
0-12,16-30	1	87.1	0	0	хорошее
0-30,40	1	75.6	0	0	отличное

изменено 11.11.2017