Восстановление электронной плотности
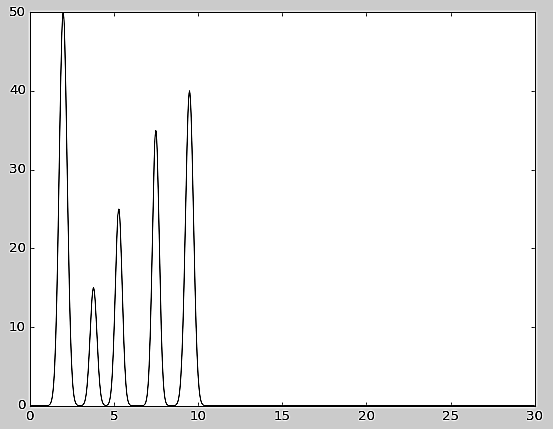
На отрезке [0,30] (ангстремы) расположены две молекулы. Две молекулы (всего 5 атомов) расположены на расстоянии ~ 5 ангстрем. Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме. Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py:
compile-func.py -g 15,3.5,3.8+25,3.5,5.3+35,3.5,7.5+40,3,9.5+50,3,2
На выходе скрипта получаем текстовый файл func.txt, в котором заданы пары (Х,Y) функции. Так же скрипт выдает график функции ЭП, который приведен ниже.

График электронной плотности для заданной молекулы
Полные наборы гармоник
Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py:
func2fourier.py -i func1.txt -o fourier1.txt
В выходном файле fourier1.txt приведены номер каждой гармоники, её амплитуда и фаза.
Было получено 499 гармоник. Далее нужно было определить n0 - число гармоник, при котором восстановление отличное. Проверялись n0 =1, 10, 20, 30, 40, 60. Ниже представлены графики, показывающие восстановленные функции электронной плотности. n0 было определенно равным 40.
Чтобы определить минимальный необходимый для восстановления функции набор гармоник n0, использовался скрипт fourier-filter.py. Набор команд:commands.txt.
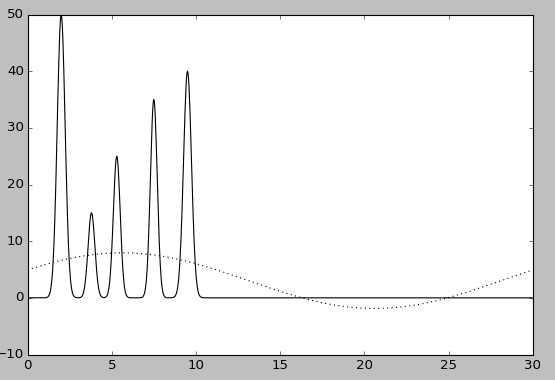
n0=1.
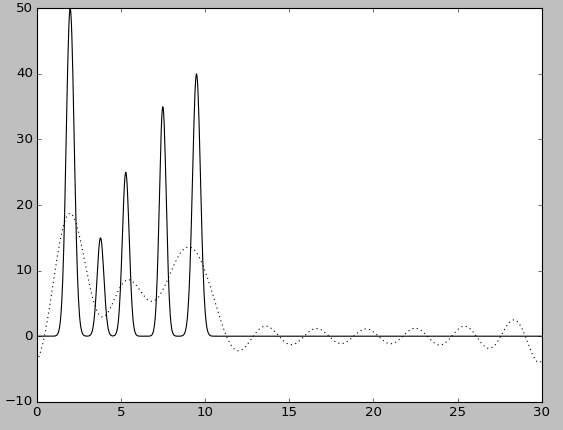
n0=10.
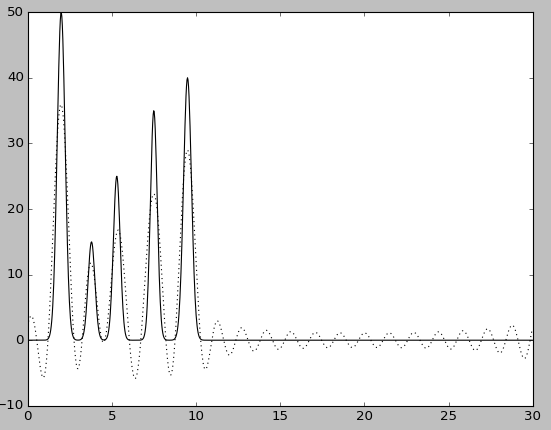
n0=20.

n0=30.
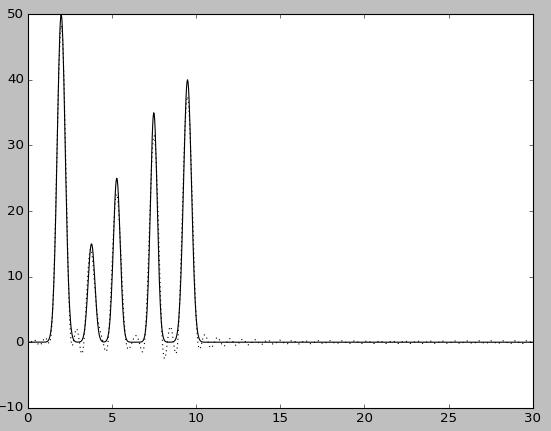
n0=40.
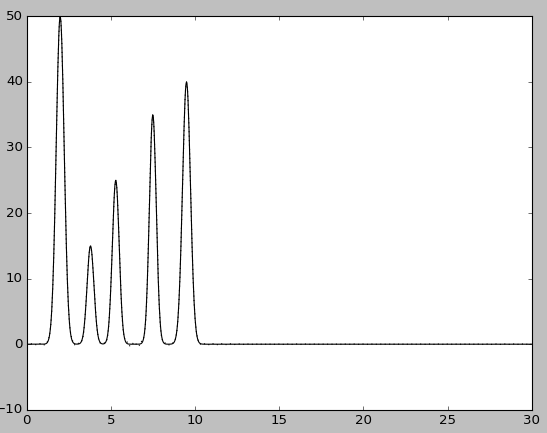
n0=60.
Восстановление для n0 = 1, n 0= 10 является плохим, так как положение атомов определить невозможно. При n0 = 20 можно определить положение лишь некоторых атомов, при n0 = 30 по восстановленной функции можно угадать положение всех максимумов, зная число слагаемых, однако на восстановленной функции максимумы некоторых «атомов» плохо отличимы от шума. При n0 = 40 можно определить положение максимума всех гауссовых слагаемых функции, что говорит об отличном восстановлении. Использование больших значений n0 для полных наборов гармоник позволяет ещё более точно восстановить исходную функцию (n0 = 60).
К амплитудам и фазам был добавлен шум (параметры -F и P скрипта func2fourier.py соответственно). Графики электронных плотностей, восстановленных по полному набору гармоник (n0=40) с шумом представлены ниже.
Список команд:commands1.txt
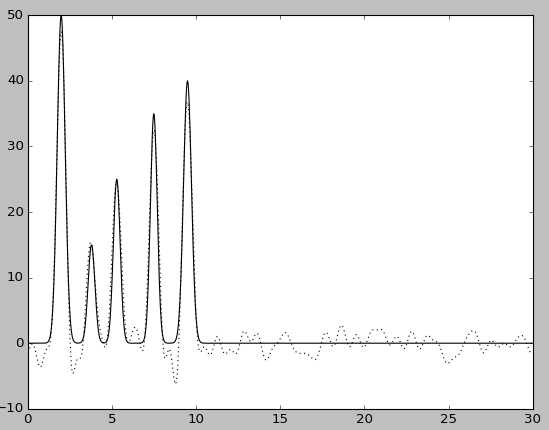
Шум -F 20
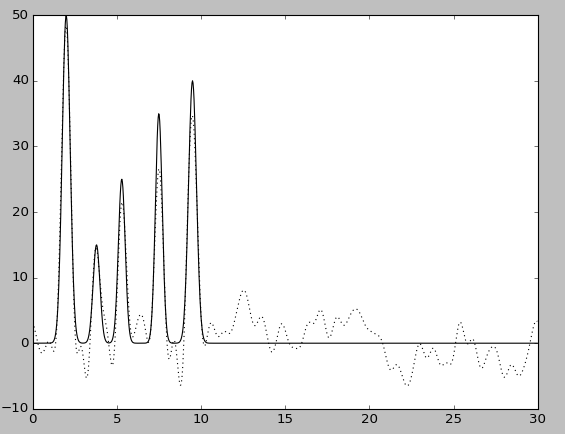
Шум -P 20
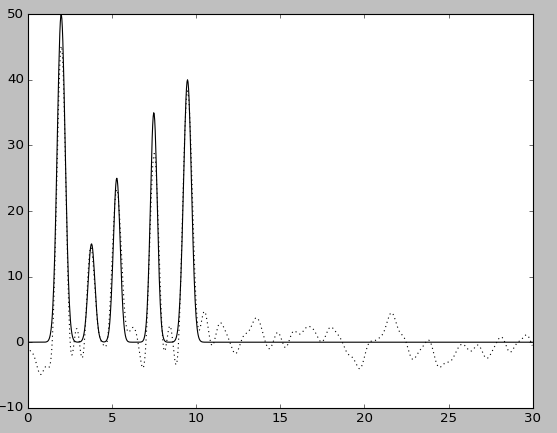
Шум -F 10 -P 10
Таким образом, можно заметить, что качество восстановления заметно снизилось.
Неполные наборы гармоник
Для получения неполного набора гармоник удалили одну и две начальные гармоники. Список команд: commands2.txt.
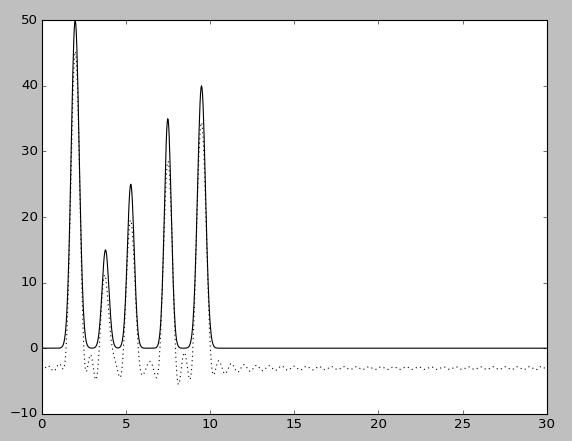
Удаление первой гармоники n=0
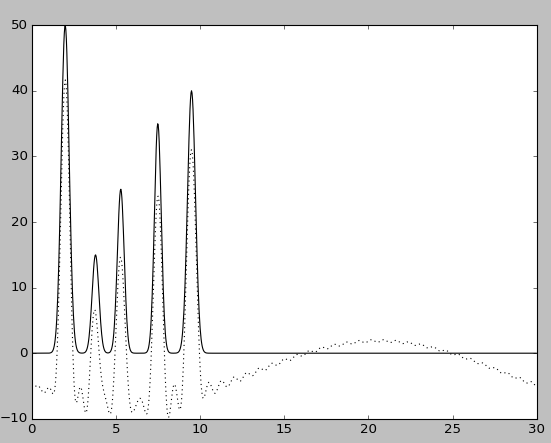
Удаление гармоник n=0 и n=1
В обоих случаях восстановление отличное, но при удалении двух гармоник функция заметно искажается, значения максимумов можно однозначно определить
Из набора удалили гармоники с номерами 29-30 (5%) и гармоники с номерами 21-24(10%). Список команд: commands3.txt.
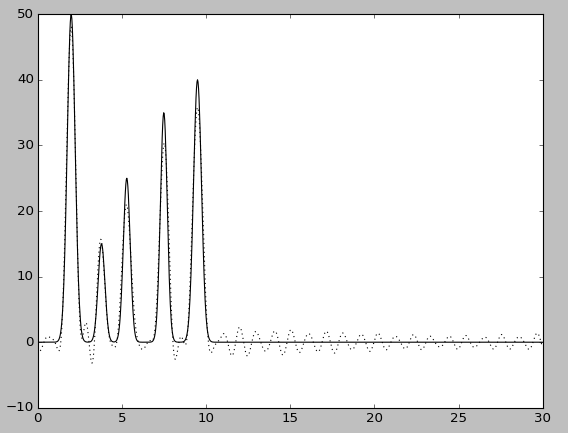
Уаление 29-30 гармоник
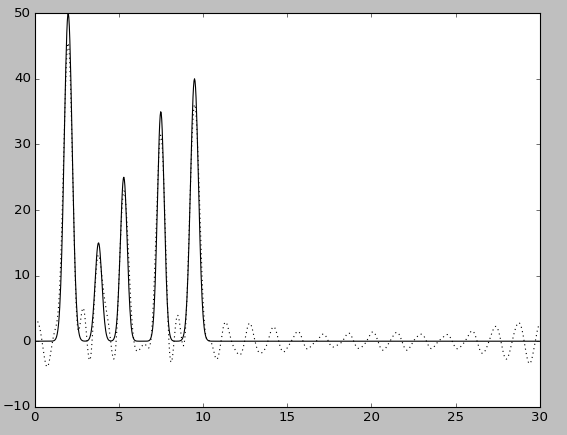
Удаление 21-24 гармоник
В обоих случаях качество восстановления становится средним.При этомвследствие удаления гармоник в середине набора максимумы от «атомов» становятся менее отличимы от шума.
К набору добавили гармонику с номером 50. Список команд: commands4.txt
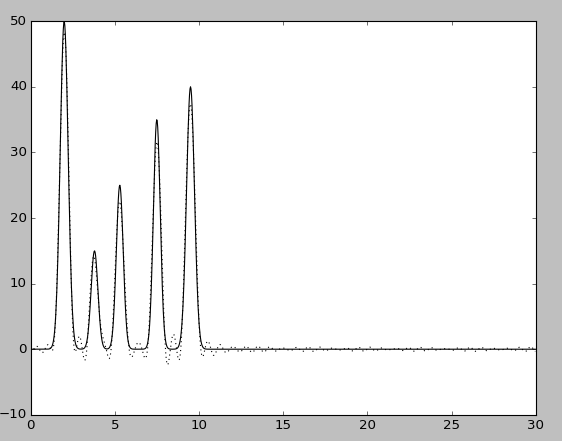
Добавление гармоники n0+10
Результат практически не отличается от того, что получается при восстановлении по полному набору гармоник.
Определение разрешения и полноты данных
По результатам анализа восстановления от исходных данных была заполнена таблица ниже.
| Набор гармоник | Разрешение, A | Полнота данных, % | Шум амплитуды (% от F) | Шум фазы (% от phi) | Качество восстановления | |
| Полный набор гармоник | 0-1 | 30 | 100 | 0 | 0 | Плохое |
| 0-10 | 3 | 100 | 0 | 0 | Плохое | |
| 0-20 | 1.5 | 100 | 0 | 0 | Среднее | |
| 0-30 | 1 | 100 | 0 | 0 | Хорошее | |
| 0-40 | 0.75 | 100 | 20 | 0 | Среднее | |
| 0-40 | 0.75 | 100 | 0 | 20 | Среднее | |
| 0-40 | 0.75 | 100 | 10 | 10 | Среднее | |
| Неполный набор гармоник | 1-40 | 0.75 | 97.75 | 0 | 0 | Отличное |
| 2-40 | 0.75 | 95 | 0 | 0 | Отличное | |
| 0-28, 31-40 | 0.75 | 95 | 0 | 0 | Хорошее | |
| 0-20, 25-40 | 0.75 | 90 | 0 | 0 | Хорошее | |
| 0-40, 50 | 0.75 | 100 | 0 | 0 | Отличное |
Для полного набора гармоник разрешение определяется как период гармоники с наибольшим номером. Тогда, например, разрешение для полного набора гармоник 0, 1, ..., 40 равно 30 ангстрем / 40 = 0,75 ангстрем (в данном компьютерном эксперименте). Полнота данных вычисляется как процент гармоник в наборе, период которых не меньше разрешения, от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%.
Для неполного набора гармоник разумно всегда указывать, помимо разрешения, полноту данных. Так, для набора гармоник 0, 1, ..., 40, 50 разрешение можно определить равным ~0,60 ангстрем при полноте данных 80%. Однако более «справедливым» выглядит разрешение ~0,75 ангстрем при полноте данных 100%. Таким образом, при указании разрешения для неполного набора гармоник видится разумным использование некоего условного порога на полноту данных (например, в 90%).