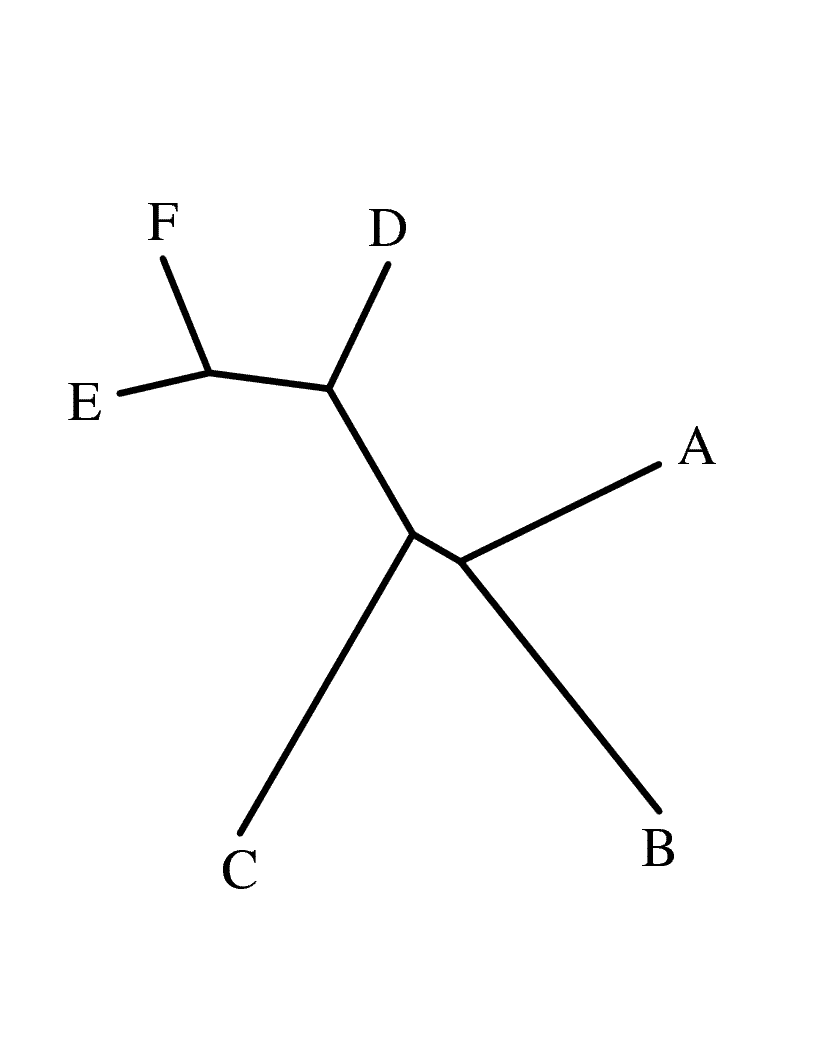
Это неукоренённое дерево.
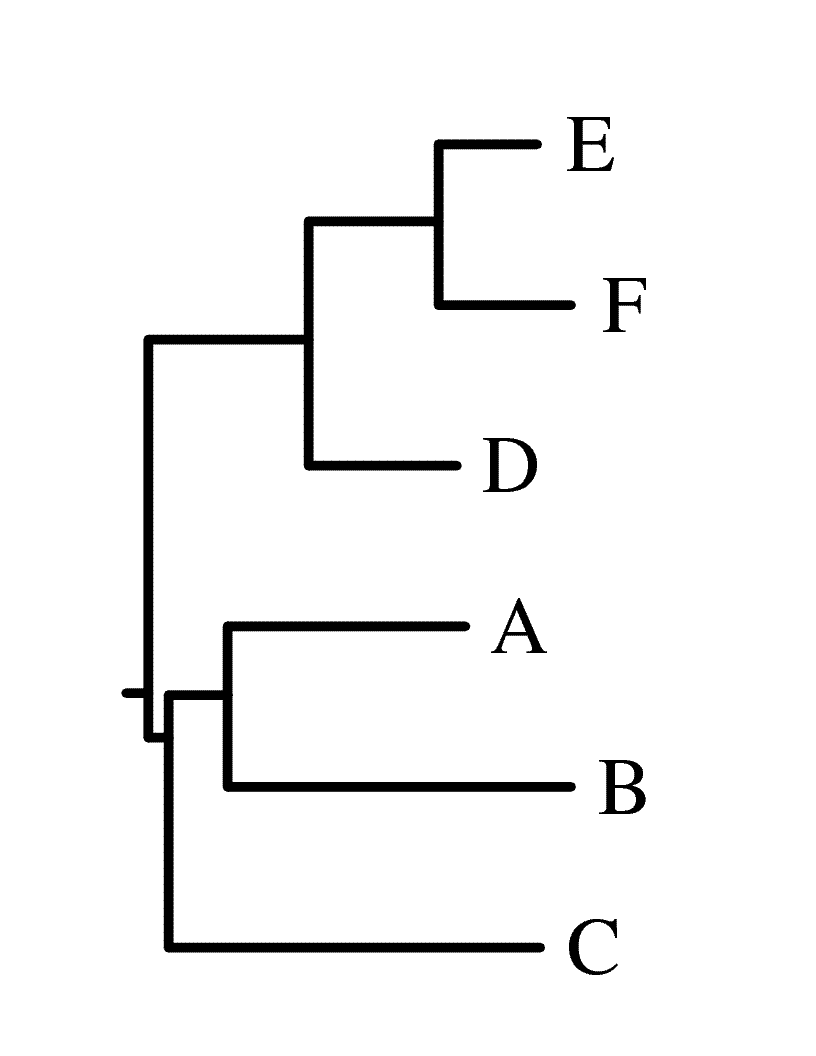
А это филограмма.
+-------------D
+100.0-|
| | +------F
+-86.0-| +100.0-|
| | +------E
+------| |
| | +--------------------C
| |
| +---------------------------A
|
+----------------------------------B
Нетрудно заметить, что топология бутстрэпного дерева полностью совпадает с
топологией реального дерева. Более того, мы можем доверять этому дереву "как
самому себе" — ведь бутстрэпное значение одной ветви равно 86 (т.е.
ветвь надёжна, и даже очень!), а двух других — вообще по сотне!!!Species in order: 1. B 2. D 3. F 4. E 5. C 6. AА вот бутстреп-значения из выходного файла:
Set (species in order) How many times out of 100.00 ..**.. 100.00 .***.. 100.00 .****. 86.00На этих данных и базируются приведённые мной выводы о полученном бутстрепном дереве. Небольшое пояснение: сначала приведён порядок листьев, а потом топология, где внутренние ветви расставлены согласно этому порядку.
1. E 2. F 3. D 4. B 5. C 6. AВот топология дерева согласно этому порядку:
Set (species in order) How many times out of 100.00 ..**** 100.00 ...*** 100.00 ...*.* 81.00Были также получены ветви, которые явно не являются достоверными (согласно их значениям).
Set (species in order) How many times out of 100.00 ....** 17.00 ...**. 2.00И наконец, то, ради чего всё это было затеяно — само филогенетическое дерево.
+--------------------D
+100.0-|
| | +-------------C
| +100.0-|
+------| | +------A
| | +-81.0-|
| | +------B
| |
| +---------------------------F
|
+----------------------------------E
Можно заметить, что топология построенного дерева полностью соответствует
топологии как реального дерева, так и полученного в пункте 1. Правда, оно чуть-
чуть менее достоверно — вместо значения, равного 86, ветвь, соединяющая
две группы листьев — (A,B) и (C,D,E,F) — принимает значение, равное
81. Но разброс данных по методу Jackknife больше, потому что появились ещё две
возможные ветви (хотя они и недостоверные).(C:0.73782,((E:0.19591,F:0.26319):0.25757,D:0.29418):0.35843,(A:0.47201, B:0.68159):0.11738)Далее опишем программы, которые нам помогли в работе:
 Это неукоренённое дерево. |
 А это филограмма. |
+----------D
+----------------4
| | +--------F
+-----2 +--------3
| | +------E
| |
| +------------------------------C
|
1---------------------------B
|
+--------------------A
и исходное дерево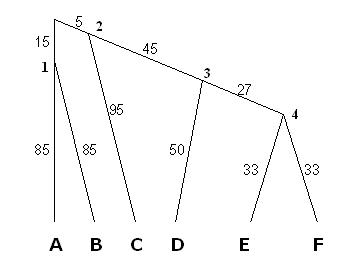
Корень дерева ближе всего находится к узлу 2. Поэтому мы возьмём
последовательность, восстановленную в узле 2, как исходную (предковую).
Причина банальна: dnaml не восстанавливает последовательность в корне дерева...
Вот выравнивание данной последовательности с исходной,
полученное с помощью программы needle. Идентичность этих последовательностей
получилась очень маленькой — 59.6%. Я предполагаю, что это можно объяснить,
во-первых, приличным расстоянием от корня до листьев (100 или 110), и,
во-вторых, тем, что в выравнивании встречаются символы, не обозначающие
конкретный нуклеотид (A, T, C или G), а значит, программа не
смогла точно определить, какой нуклеотид находится в этой позиции.
Приведу обозначения этих коварных символов:
Y - пиримидин
R - пурин
S - C или G
W - A или T
M - А или С
K - G или T