Что такое филогенетическое дерево
Отобранные бактерии
| Название | Мнемоника |
| Bacillus subtilis | BACSU |
| Clostridium botulinum | CLOB1 |
| Enterococcus faecalis | ENTFA |
| Geobacillus kaustophilus | GEOKA |
| Lactobacillus acidophilus | LACAC |
| Lactococcus lactis | LACLM |
| Staphylococcus epidermidis | STAES |
| Streptococcus pneumoniae | STRPN |
Скобочная формула дерева
(CLOB1,((LACAC,(ENTFA,(LACLM,STRPN))),(STAES,(BACSU,GEOKA))));
Изображение дерева
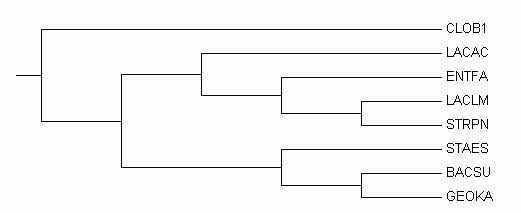
Ветви дерева
Дерево содержит 5 нетривиальных ветвей:1) {BACSU, GEOKA } vs { STAES, CLOB1, LACLM, STRPN, ENTFA, LACAC }
2) {BACSU, GEOKA, STAES } vs { CLOB1, LACLM, STRPN, ENTFA, LACAC }
3) {BACSU, GEOKA, STAES, CLOB1 } vs { LACLM, STRPN, ENTFA, LACAC }
4) {BACSU, GEOKA, STAES, CLOB1, LACAC } vs { LACLM, STRPN, ENTFA }
5) {BACSU, GEOKA, STAES, CLOB1, LACAC, ENTFA } vs { LACLM, STRPN }
Реконструкция филогенетических деревьев
Таксономия выбранных бактерий
Использованный таксономический сервис NCBI http://www.ncbi.nlm.nih.gov/taxonomy/:| Мнемоника | Таксономия |
| BACSU | cellular organisms; Bacteria; Firmicutes; Bacilli; Bacillales; Bacillaceae; Bacillus; Bacillus subtilis group |
| CLOB1 | cellular organisms; Bacteria; Firmicutes; Clostridia; Clostridiales; Clostridiaceae; Clostridium |
| ENTFA | cellular organisms; Bacteria; Firmicutes; Bacilli; Lactobacillales; Enterococcaceae; Enterococcus |
| GEOKA | cellular organisms; Bacteria; Firmicutes; Bacilli; Bacillales; Bacillaceae; Geobacillus |
| LACAC | cellular organisms; Bacteria; Firmicutes; Bacilli; Lactobacillales; Lactobacillaceae; Lactobacillus |
| LACLM | cellular organisms; Bacteria; Firmicutes; Bacilli; Lactobacillales; Streptococcaceae; Lactococcus |
| STAES | cellular organisms; Bacteria; Firmicutes; Bacilli; Bacillales; Staphylococcaceae; Staphylococcus |
| STRPN | cellular organisms; Bacteria; Firmicutes; Bacilli; Lactobacillales; Streptococcaceae; Streptococcus |
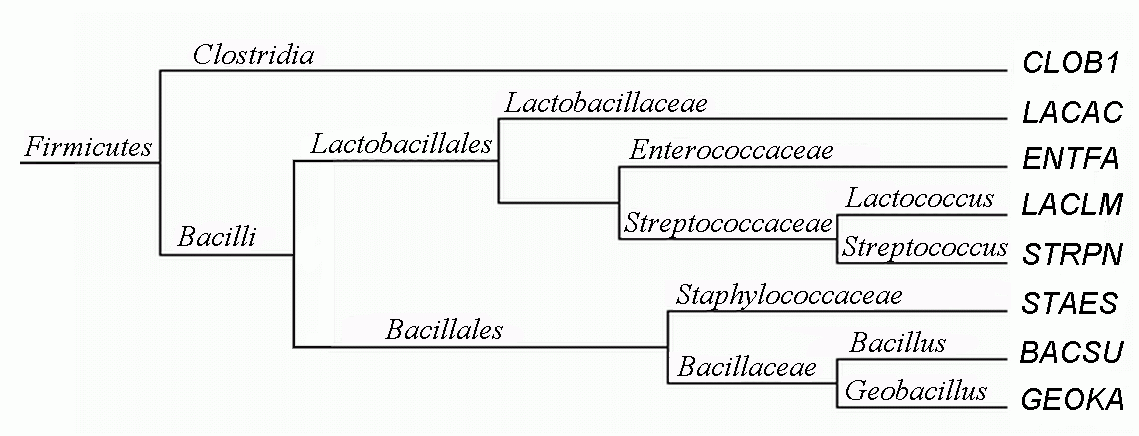
Для реконструирования филогенетического дерева было выбрано семейство белков IF2 (Фактор инициации трансляции 2) и создано выравнивание с помощью программы muscle
Поиск диагностических позиций выравнивания
РезультатыРеконструкция дерева программой fprotpars
Скобочная формула дерева
Программа выдала только одно дерево(((ENTFA,(GEOKA,(STAES,(BACSU,CLOB1)))),(STRPN,LACLM)),LACAC);
Изображение дерева
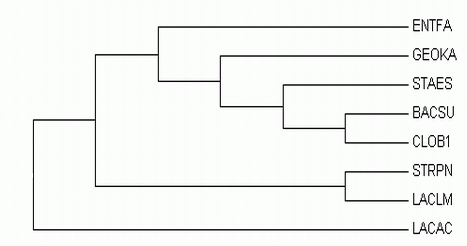
Комментарии :
Топология этого дерева совпалает с правильной только по двум ветвям:
{BACSU, GEOKA, STAES, CLOB1 } vs { LACLM, STRPN, ENTFA, LACAC }
{BACSU, GEOKA, STAES, CLOB1, LACAC, ENTFA } vs { LACLM, STRPN }
Ветви, которые есть в дереве, построенном fprotpars, но отсутствуют в правильном:
{BACSU, CLOB1 } vs { STAES, GEOKA, LACLM, STRPN, ENTFA, LACAC }
{BACSU, CLOB1, STAES } vs { GEOKA, LACLM, STRPN, ENTFA, LACAC }
{BACSU, GEOKA, STAES, CLOB1, ENTFA } vs { LACLM, STRPN, LACAC }
Ветви, которые есть в правильном дереве, но отсутствуют в дереве, построенном fprotpars:
{BACSU, GEOKA } vs { STAES, CLOB1, LACLM, STRPN, ENTFA, LACAC }
{BACSU, GEOKA, STAES } vs { CLOB1, LACLM, STRPN, ENTFA, LACAC }
{BACSU, GEOKA, STAES, CLOB1, LACAC } vs { LACLM, STRPN, ENTFA }
*Рассматривались только нетривиальные ветви.
Оценка эволюционных расстояний между последовательностями программой fprotdist
Матрица расстояний, полученная программой fprotdist
| LACAC | LACLM | CLOB1 | STAES | GEOKA | BACSU | ENTFA | STRPN | |
| LACAC | 0.000000 | 0.879882 | 0.816413 | 0.711764 | 0.691780 | 0.688026 | 0.653347 | 0.795011 |
| LACLM | 0.879882 | 0.000000 | 0.860399 | 0.663668 | 0.730750 | 0.674451 | 0.589780 | 0.644758 |
| CLOB1 | 0.816413 | 0.860399 | 0.000000 | 0.613374 | 0.677098 | 0.627131 | 0.736244 | 0.759876 |
| STAES | 0.711764 | 0.663668 | 0.613374 | 0.000000 | 0.499841 | 0.405165 | 0.551165 | 0.592610 |
| GEOKA | 0.691780 | 0.730750 | 0.677098 | 0.499841 | 0.000000 | 0.411840 | 0.600128 | 0.648623 |
| BACSU | 0.688026 | 0.674451 | 0.627131 | 0.405165 | 0.411840 | 0.000000 | 0.568069 | 0.604269 |
| ENTFA | 0.653347 | 0.589780 | 0.736244 | 0.551165 | 0.600128 | 0.568069 | 0.000000 | 0.544889 |
| STRPN | 0.795011 | 0.644758 | 0.759876 | 0.592610 | 0.648623 | 0.604269 | 0.544889 | 0.000000 |
Оценка ультраметричности
Ультраметричность : из трёх расстояний между тремя объектами два всегда равны между собой и не меньше третьегоd(A,B) >= d(B,C) то d(A,C) = d(A,B).
d(CLOB1,BACSU) = 0.627131
d(BACSU,GEOKA) = 0.411840
d(CLOB1,GEOKA) = 0.677098
Из трёх расстояний два почти равны между собой (отклонение на 0.049967) и не меньше третьего => принцип ультраметричности выполняется
d(STAES,GEOKA) = 0.499841
d(STAES,BACSU) = 0.405165
d(BACSU,GEOKA) = 0.411840
Из трёх расстояний два почти равны между собой (отклонение на 0.006675), но меньше третьего => принцип ультраметричности НЕ выполняется
Оценка аддитивности
Аддитивность : если есть четыре последовательности A,B,C,D, то из трёх сумм d(A,B)+d(C,D) , d(A,C)+d(B,D) , d(A,D)+d(B,C) две равны между собой и больше третьей.d(A,B)+d(C,D) = d(CLOB1,BACSU) + d(STAES,GEOKA) = 0.627131 + 0.499841 = 1.126972
d(A,C)+d(B,D) = d(CLOB1,STAES) + d(BACSU,GEOKA) = 0.613374 + 0.411840 = 1.025214
d(A,D)+d(B,C) = d(CLOB1,GEOKA) + d(BACSU,STAES) = 0.677098 + 0.405165 = 1.082263
Из трёх сумм d(A,B)+d(C,D) , d(A,C)+d(B,D) , d(A,D)+d(B,C) две почти равны между собой (отклонение на 0.044709) и больше третьей => принцип аддитивности выполняется
Реконструкция дерева программой fneighbor
Алгоритм Neighbor-Joining
По умолчанию выдаёт неукоренённое дерево с длинами ветвей; не предполагает молекулярных часов.
Полностью совпадает с правильным, если укоренить в место, отмеченное стрелочкой.
Алгоритм UPGMA
выдаёт укоренённое дерево с длинами ветвей. Его можно применять, если справедлива гипотеза молекулярных часов, т.е. матрица расстояний не слишком далека от ультраметрической.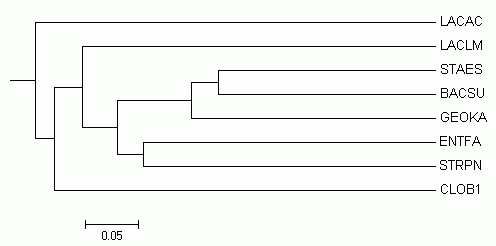
Cовпадает с правильным ( и с построенным по алгоритму Neighbor-Joining) только одной ветвью : {BACSU, GEOKA, STAES} vs {CLOB1, LACLM, STRPN, ENTFA, LACAC}. С деревом, построенным с помощью программы fprotpars, не совпадает ни одна ветвь.
Выводы: Правильным оказался только результат алгоритма Neighbor-Joining; деревья, полученные с помошью других программ, к сожалению, далеки от правильного.