Восстановление функции по коэффициентам ее ряда Фурье
Задача
Исследовать качество восстановления функции одной переменной в зависимости от того, какие и сколько гармоник ряда Фурье используются для ее восстановления.
Для этого необходимо симулировать эксперимент по получению данных об амплитудах и фазах гармоник Фурье и восстановить по ним функцию ЭП.
Модель для компьютерного эксперимента
- Для симуляции использовалась модель одномерной электронной плотности.
- На отрезке от 0 до 30 (ангстрем) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними).
- Функция имеет вид нескольких гауссовых кривых с центром в разных точках. Электронные плотности (ЭП) атомов описываются этими гауссовыми кривыми, которые представляют собой пики на графике.
- Гауссова функция определяется числами lambda,beta,gamma (параметрами) по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2)
- Параметры гауссовских кривых соответствуют различным атомам. Различная высота пиков соответствует различному количеству электронов в атоме, ширина пика примерно соответствует диаметру атома, то есть порядка 1 ангстрема(электронная плотность резко спадает на таком расстоянии от центра).
Симуляция
Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py (из пяти пиков - 3+2, всего две "молекулы" - модель водородной связи (3.5) ):
python compile-func.py -g 16,3.5,4.72+12,3.5,6.54+14,3.5,7.82+1,3,11.32+14,3.5,12.33
Каждое "слагаемое" в формуле для параметра -g соответствует одному атому (пику) и содержит в себе параметры, разделенные запятыми:
- высота пика (число электронов)
- ширинa пика (размер атома)
- положение пика на прямой (так как симуляция одномерная)
Выходной файл скрипта compile-func.py - текстовый файл func.txt, в котором описана заданная функция (в виде пар X – Y).
 |
| Рис.1. Функция электронной плотности атомов двух воображаемых молекул на отрезке [0;30] |
Экспериментальной информацией, на самом деле, являются данные об амплитудах и фазах гармоник Фурье. Коэффициенты Фурье можно рассчитать при помощи скрипта func2fourier.py. В результате получается файл вида garm.txt:
#no. F phi
0 4.72654359376 0
1 1.39720718995 -2.12035906411
2 1.98245142474 -1.43298013822
3 0.433019796648 1.19952810495
4 1.16454822148 -2.28301295427
5 0.827520704547 -2.09439511117
python func2fourier.py -i func.txt -o garm.txt
Выходной файл имеет формат:
<номер гармоники> <амплитуда> <фаза>
Добавление гауссового шума к амплитудам (параметр -F <число>) и фазам (-P <число>) искажает все вычисленные амплитуды и фазы. Пример: -F 20 (шум 20%) приводит к тому, что к каждой амплитуде прибавляется случайное число, распределенное нормально с параметрами: среднее = 0, среднее квадратичное отклонение (сигма)=0.2*F. Аналогично действует параметр -P <число>. Это позволяет еще более точно приблизится к эксперименту.
Восстановление функции электронной плотности. Полные наборы гармоник.
Для сравнения восстановленной функции с исходной использовались следующие категории:
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов").
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума.
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно.
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".
Коэффициенты ряда Фурье рассчитаны при помощи скрипта func2fourier.py. Результат - файл garm_full.txt:
python func2fourier.py -i func.txt -o garm_full.txt -F 0 -P 0
Из 499 гармоник отбиралось n0 гармоник (полный набор - 0, 1, ..., n0), для которых по графику восстановленной по ним функции можно было определить положение максимумов всех гауссовых слагаемых («отличное восстановление»):
python fourier-filter.py -r 0-15 -i garm_full.txt -o garm_full_0-15.txt
python fourier2func.py -f func.txt -i garm_full_0-15.txt -o recr_func_0-15.txt -s
 |
|

|
|
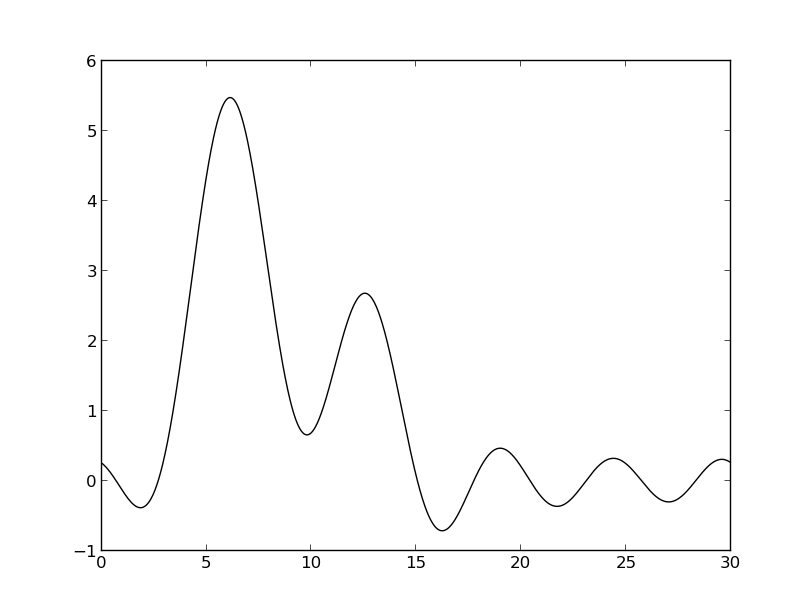
Исходная функция
|
n0 = 5 (плохое)
|
n0 = 10 (плохое)
|

|

|
|
|
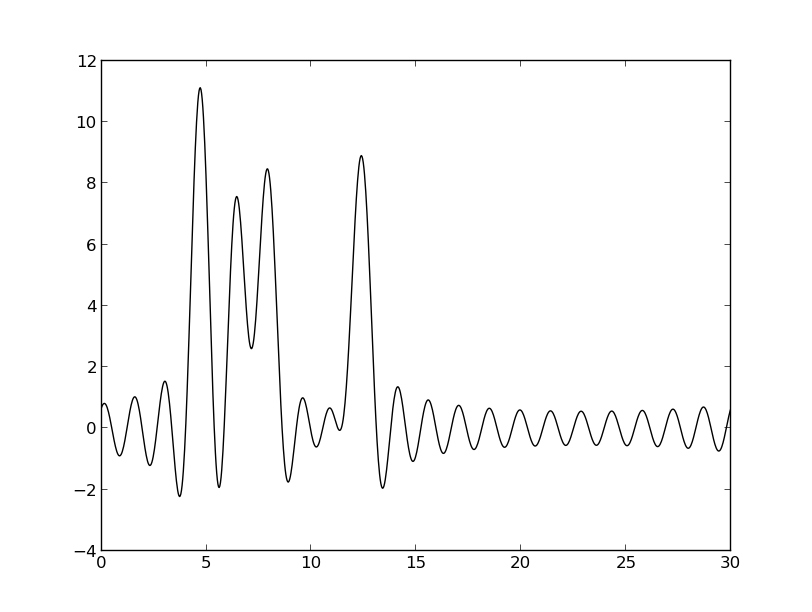
Исходная функция
|
n0 = 15 (плохое)
|
n0 = 20 (среднее)
|

|

|
|
|
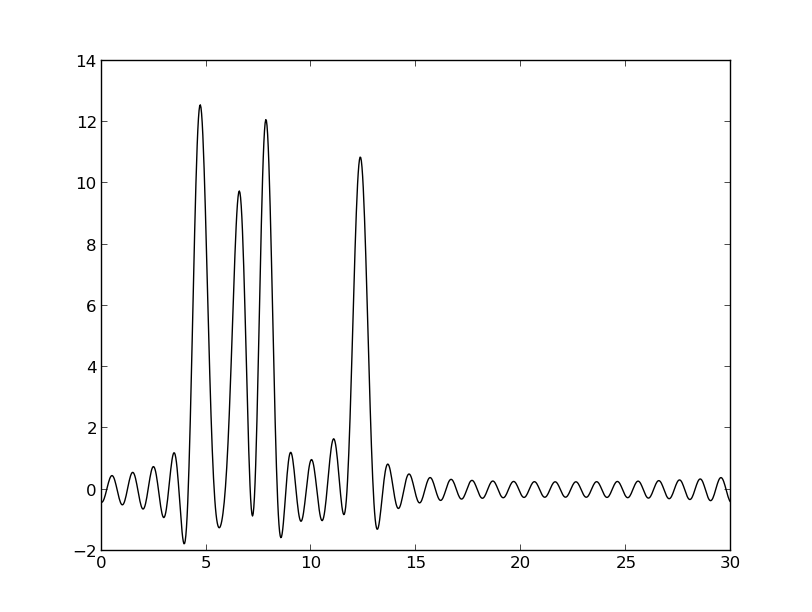
Исходная функция
|
n0 = 25 (среднее)
|
n0 = 30 (хорошее)
|

|

|

|
|
Исходная функция
|
n0 = 35 (хорошее)
|
n0 = 40 (хорошее)
|

|

|

|
|
Исходная функция
|
n0 = 45 (отличное)
|
n0 = 70 (отличное)
|
Таким образом, четыре пика для тяжелых атомов хорошо различимы уже на n = 20, но пик легкого атома выделяется только при n = 45, поэтому за минимальный полный набор гармоник примем n0=45. Таким образом, основная трудность - разрешение соседних пиков, а также отличие пиков малых атомом (водород) от шума.
Если брать еще большие значения n для полных наборов гармоник, то восстановить исходную функцию получается еще точнее.
Добавление шума
Теперь добавим шум к амплитудам и фазам. По полному набору гармоник (0-45) были построены графики восстановленной функции при ненулевом значении шума.
# Добавление шума к амплитуде
python func2fourier.py -F 20 -i func.txt -o ampl_noise20.txt
python fourier-filter.py -r 0-45 -i ampl_noise20.txt -o ampl_noise20_45.txt
python fourier2func.py -i ampl_noise20_45.txt -o recr_func_ampl_noise20_45.txt -s
# Добавление шума только к фазе
python func2fourier.py -P 20 -i func.txt -o phase_noise20.txt
python fourier-filter.py -r 0-45 -i phase_noise20.txt -o phase_noise20_45.txt
python fourier2func.py -i phase_noise20_45.txt -o recr_func_phase_noise20_45.txt -s
# Добавление шума к амплитуде и к фазе
python func2fourier.py -F 20 -P 20 -i func.txt -o both_noise20.txt
python fourier-filter.py -r 0-45 -i both_noise20.txt -o both_noise20_45.txt
python fourier2func.py -i both_noise20_45.txt -o recr_func_both_noise20_45.txt -s

|

|

|
|
Исходная функция
|
Нет шума
|
Шум амплитуды 20 %
|

|

|

|
|
Исходная функция
|
Шум фазы 20 %
|
Шум амплитуды и фазы 20 %
|
Из рисунков видно, что ошибка в фазе больше "мешает" верно определить пики, чем такой же шум в амплитуде. Поэтому решение проблемы фаз в настоящем эксперименте - важная задача, так как неверное определение фазы сильно влияет на результат.
Неполные наборы гармоник. Удаление первых гармоник
Удаление первых (0, 0-1, 0-3) гармоник поможет понять, как первые гармоники влияют на качество результата.
# Удаление первой гармоники
python fourier-filter.py -r 1-45 -i garm_full.txt -o garm_1-45.txt
python fourier2func.py -i garm_1-45.txt -o recr_func_1-45.txt -s
# Удаление первых двух гармоник
python fourier-filter.py -r 2-45 -i garm_full.txt -o garm_2-45.txt
python fourier2func.py -i garm_2-45.txt -o recr_func_2-45.txt -s
# Удаление первых трех гармоник
python fourier-filter.py -r 3-45 -i garm_full.txt -o garm_3-45.txt
python fourier2func.py -i garm_3-45.txt -o recr_func_3-45.txt -s
 |
 |
 |
| Исходная функция |
Гармоники 0-45 |
Гармоники 1-45 |
 |
 |
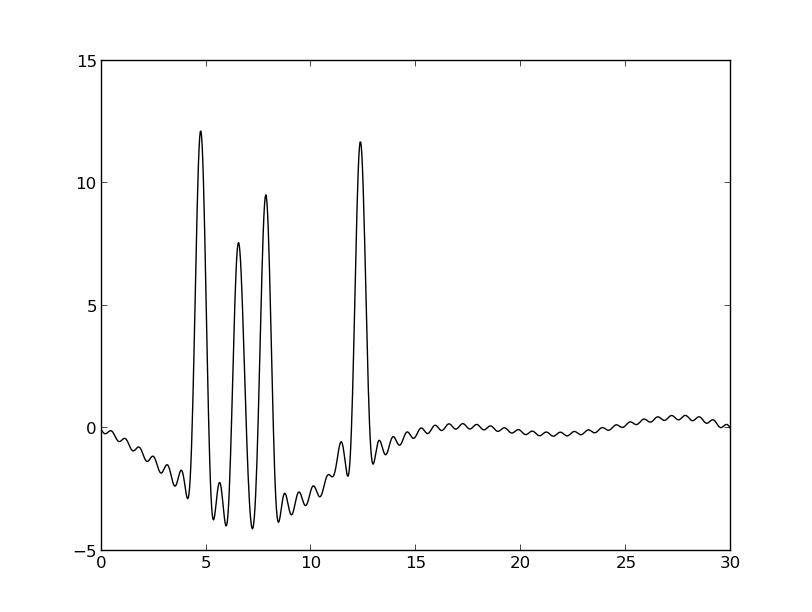 |
| Исходная функция |
Гармоники 2-45 |
Гармоники 3-45 |
При удалении первой гармоники функция смещается по оси ординат; при этом результат восстановления можно считать «отличным».
При удалении первых двух и трех гармоник восстановленная функция сильно искажается, но значения максимумов для больших атомов можно однозначно определить (водород, как и ожидается, не отличим от шума).
Такомобразом, удаление первых гармоник значительно искажает фоновое значение (фон теперь не образует "прямую" вдоль оси абсцисс) и увеличивается шум.
Неполные наборы гармоник. Удаление гармоник из середины набора
Было решено удалить 6,7% и 11,1% гармоник из середины набора (гармоники 16, 24 и 32 (6%), 8, 40 (12%)). Такое удаление гармоник не дает никакого радикального эффекта, хоть разрешение, а значит и качество восстановления, снижается вследствие неполноты данных (можно охарактеризовать как «среднее»). Таким образом, удаление гармоник в середине набора приводит к тому,что максимумы от «атомов» становятся менее отличимы от фонового шума, вследствие его увеличения.
# Удаление 6,7% гармоник
python fourier-filter.py -r 0-15,17-23,25-31,33-45 -i garm_full.txt -o garm_6.txt
python fourier2func.py -i garm_6.txt -o recr_func_6.txt -s
# Удаление 11,1% гармоник
python fourier-filter.py -r 0-7,9-15,17-23,25-31,33-39,41-45 -i garm_full.txt -o garm_11.txt
python fourier2func.py -i garm_11.txt -o recr_func_11.txt -s
 |
 |
| Исходная функция |
Полный набор гармоник (0...45) |
 |
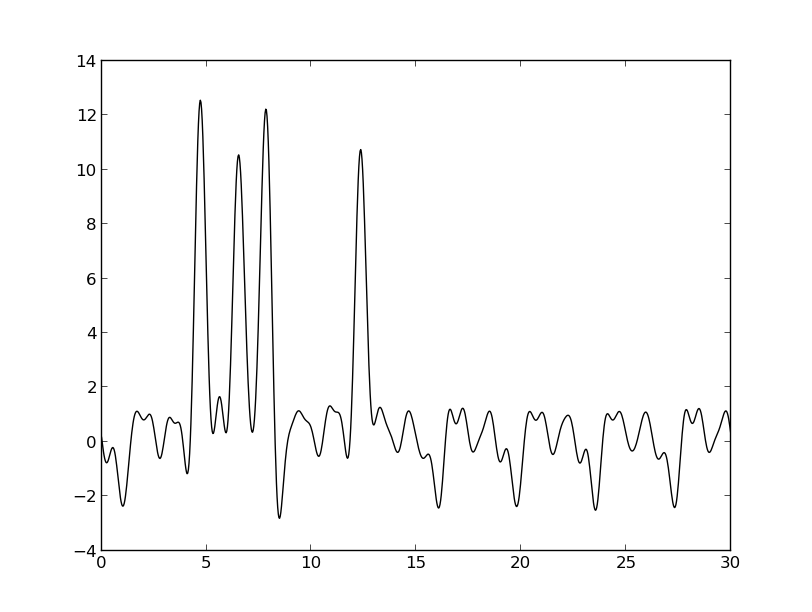 |
| 6,7% гармоник удалено |
11,1% гармоник удалено |
Добавление гармоники n0+10
К набору гармоник 0-45 добавлена гармоника 55, что ни в коей мере не изменило качество восстановления.
# Добавление 55 гармоники
python fourier-filter.py -r 0-45,55 -i garm_full.txt -o garm_55.txt
python fourier2func.py -i garm_55.txt -o recr_func_55.txt -s
 |
 |
 |
| Исходная функция |
Полный набор гармоник (0...45) |
Гармоники (0...45, 55) |
Таблица 1. Восстановление функции по коэффициентам ряда Фурье
| Набор гармоник |
Разрешение, A |
Полнота данных,% |
Шум амплитуды (% от F) |
Шум фазы (% от phi) |
Качество восстановления |
| Полный набор гармоник |
| 0-5 |
6 |
100 |
0 |
0 |
Плохое |
| 0-10 |
3 |
100 |
0 |
0 |
Плохое |
| 0-15 |
2 |
100 |
0 |
0 |
Плохое |
| 0-20 |
1.5 |
100 |
0 |
0 |
Среднее |
| 0-25 |
1.2 |
100 |
0 |
0 |
Среднее |
| 0-30 |
1 |
100 |
0 |
0 |
Хорошее |
| 0-35 |
0.86 |
100 |
0 |
0 |
Хорошее |
| 0-40 |
0.75 |
100 |
0 |
0 |
Хорошее |
| 0-45 |
0.67 |
100 |
0 |
0 |
Отличное |
| 0-45 |
0.67 |
100 |
20 |
0 |
Хорошее |
| 0-45 |
0.67 |
100 |
0 |
20 |
Среднее |
| 0-45 |
0.67 |
100 |
20 |
20 |
Среднее |
| Неполный набор гармоник |
| 1-45 |
0.67 |
97.82 |
0 |
0 |
Отличное |
| 2-45 |
0.67 |
95.65 |
0 |
0 |
Хорошее |
| 3-45 |
0.67 |
93.48 |
0 |
0 |
Хорошее |
| 0-15,17-23,25-31,33-45 |
0.67 |
93.48 |
0 |
0 |
Среднее |
| 0-7,9-15,17-23,25-31,33-39,41-45 |
0.67 |
89.13 |
0 |
0 |
Среднее |
| 0-45, 55 |
0.67 |
100 |
0 |
0 |
Отличное |
|