Профили подсемейства белков

Выбор Подсемейства

В начале необходимо было выбрать подсемейство из выравнивания последовательностей домена, исследованного в прошлом практикуме. Подсемейство будем считать хорошим, если оно является кладой на дереве и если есть некоторые признаки (доменная архитектура, таксономическая принадлежность или диагностические позиции), по которым можно отнести домен к данному подсемейству. Я решила выбрать выделенное на рис. 1 подсемейство. Они образуют кладу и имеют диагностические позиции (например, №105,150 и 154). Таким образом, в подсемействе 18 последовательностей. Выбранные последовательности были сохранены в отдельный файл в формате .fasta.

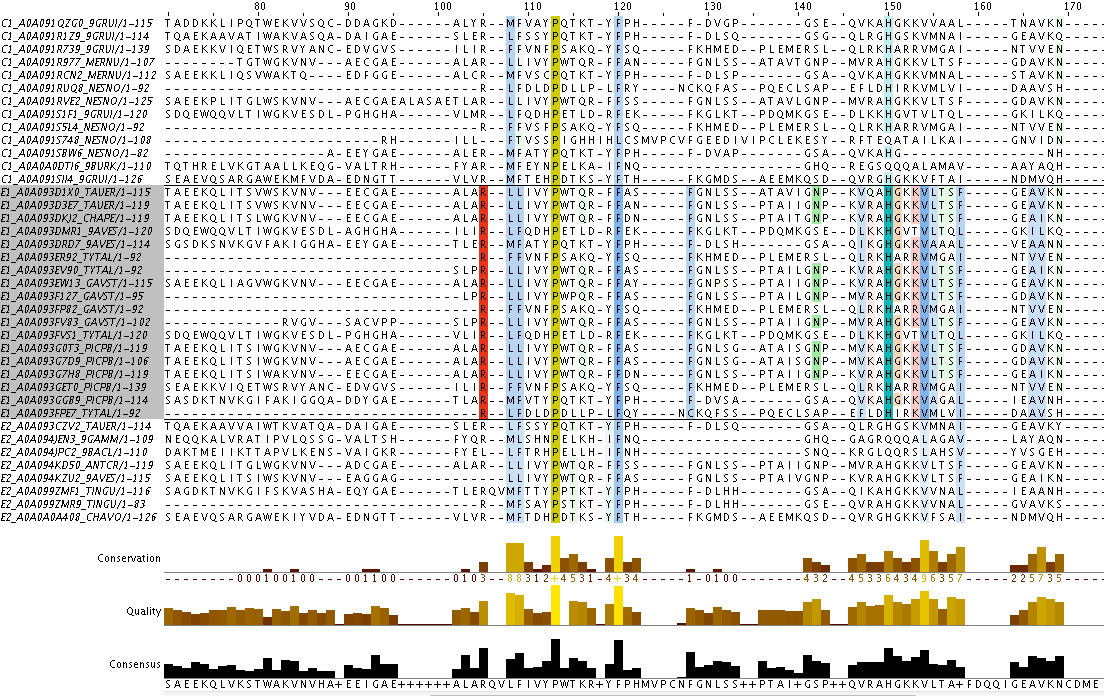Рис. 1. Выделенное в выравнивании подсемейство

Рис. 2. Отдельное выравнивание подсемейства

Построение профиля и поиск гомологов

Далее для полученного подсемейства необходимо было построить профиль. Для этого использовался пакет HMMER, использующий скрытые модели Маркова для анализа выравнивания последовательностей и поиска гомологов.

Сначала был построен профиль:

 hmm2build profile.out podsem1.fasta

Полученный файл c профилем был откалиброван:

 hmm2calibrate profile.out

Затем я скачала с сайта UniProt полноразмерные последовательности белков, содержащих мой домен.
По полученному файлу для итогового профиля был осуществлен поиск гомологов:

 hmm2search profile.out PF00042.fasta > findings.out

В итоговом файле findings.out содержатся все находки.

Анализ результатов

Для анализа результатов нам предложили использовать ROC-кривую и гистограмму весов находок.
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для анализа качества моделей. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров. Рассмотрим возможные результаты: TP (True Positives) — верно классифицированные положительные примеры (истинно положительные случаи). В нашем случае — это количество последовательностей, расположенных выше некоторого порога и достоверно содержащих искомый домен; TN (True Negatives) — верно классифицированные отрицательные примеры (истинно отрицательные случаи). В нашем случае — это количество последовательностей, расположенных ниже некоторого порога и достоверно не содержащих искомый домен; FP (False Positives) — отрицательные примеры, классифицированные как положительные (ошибка II рода); Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи). В нашем случае — это количество последовательностей, расположенных выше некоторого порога, но не содержащих домен;
FN (False Negatives) — положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый "ложный пропуск" – когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры). В нашем случае — это количество последовательностей, расположенных ниже некоторого порога и содержащих домен.
Специфичность (SP) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью (т.е. доля достоверно предсказанных белков, не содержащих домен, 2 от общего количества последовательностей, известно не содержащих этот домен).
Чувствительность (SE) — доля истинно положительных случаев (т.е. доля достоверно предсказанных белков, содержащих домен, от общего количества последовательностей,
известно содержащих домен. Из определений следуют формулы, по которым считаются данные показатели: SP = TN/(TN+FP)
SE = TP/(TP+FN)

Были проанализированы результаты поиска гомологов по профилю. Файл с находками был открыт в Excel (лист 'Лист1'), на другом листе ('Лист2') для каждого значения порога были подсчитаны TP, TN, FP и FN, а также SP и SN, а также значения 1-SP, построена ROC-кривая: по оси ОY откладывается SЕ, по оси ОX — 1–SP (сто процентов минус специфичность). Результат приведен на рис. 3. Итоговая таблица: table1.xlsx.

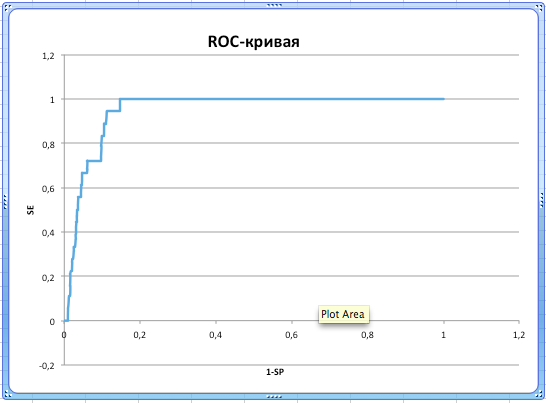
Рис. 3. Полученная ROC-кривая

Находок	принадлежит подсемейству	не принадлежит подсемейству	Сумма
Выше порога по профилю	18	340	358
Ниже порога	0	1971	1971
Сумма	18	2311	2329