Рис.
Главная страница > Четвертый семестр > Филогенетическое дерево и его реконструкция (дополнительные задания)
Для оценки статистической надежности реконструированных деревьев (см. результаты выполнения обязательных заданий) было построено 100 jackknife-реплик исходного выравнивания. Для построения реплик использовалась программа seqboot пакета PHYLIP (версия, свободно распространяемая на сайте Felsenstein lab). В связи с тем, что данная программа принимает входные файлы только в формате PHYLIP, исходное множественное выравнивание было переведено из формата FASTA в формат PHYLIP средствами GeneDoc. Использование программы seqboot вместо fseqboot связано с тем, что построенные fseqboot реплики имели длину 1830 н.п., равную длине исходного выравнивания (программа была запущена с параметром -test j). Однако, при применении метода delete-half-jackknifing должно происходить удаление половины колонок выравнивания, то есть длина реплик должна составлять 915 н.п. Следовательно, имеет место ошибка, которую можно избежать путем использования другой версии программы. Jackknife-реплики, построенные с помощью программы seqboot, имели "правильную" длину (915 н.п.). Одна из таких реплик приведена здесь.
Анализ публикаций не позволил выявить существенных преимуществ одного из методов bootstrapping и jackknifing. По результатам Farris et al. (1996) и Freudenstein et al. (2004), jackknife-значения соответствуют бутстреп-значениям тех же ветвей при удалении не половины, а 1/e столбцов исходного выравнивания (метод delete-fraction-jackknifing). Это противоречит результатам Felsenstein (2005), утверждающего, что наибольшее соответствие между jackknife- и бутстреп-значениями достигается при удалении половины столбцов (метод delete-half-jackknifing, который и реализован автором последней публикации в программе seqboot). Подробнее см. Muller (2005).
Реконструкция деревьев по построенным репликам была проведена с помощью программы fdnaml. Меньшие длины jackknife-реплик по сравнению с бутстреп-репликами существенно сократили время, затраченное на построение деревьев. Таким образом, анализ статистической надежности деревьев с помощью метода jackknifing занимает меньше времени, чем с помощью метода bootstrapping, что может оказаться существенным при работе с большим количеством последовательностей (несколько десятков) и построении большого количества реплик (более 1000).
Консенсусное дерево было построено с помощью программы fconsense (использовался метод extended majority rule, рис. 1). Топология консенсусного дерева соответствует топологии исходного дерева и реконструированных деревьев, а также консенсусного дерева, построенного методом бутстреп-анализа. Это служит дополнительным подтверждением надежности реконструкций. Jackknife-значения трех внутренних ветвей составляют 85, 90 и 100, то есть несколько ниже соответствующих бутстреп-значений (88, 97 и 100, рис. 2). При этом имеет место корреляция между длинами ветвей исходного дерева и их jackknife-значениями (о причинах см. результаты выполнения обязательных заданий). Количество ложных ветвей (не включенных в консенсусное дерево) равняется четырем (вместо трех при проведении бутстреп-анализа), и их jackknife-значения (5, 5, 7, 8) в целом несколько выше бутстреп-значений (3, 3, 9). Таким образом, деревья, реконструированные по отдельным jackknife-репликам, менее надежны, чем деревья реконструированные по отдельным бутстреп-репликам. Лучшего соответствия между jackknife- и бутстреп-значениями можно добиться путем увеличения количества информации исходного выравнивания в составе реплик (то есть путем удаления менее чем половины столбцов исходного выравнивания). Возможно, при использовании метода delete-fraction-jackknifing, который осуществляет удаление 1/e столбцов (около 44%), jackknife-значения ветвей приблизятся к бутстреп-значениям. При этом проведение анализа надежности топологии по данному методу также займет меньше времени, чем при использовании бутстреп-анализа.
|
|
Рис.
1. Визуализация консенсусного дерева. Для внутренних ветвей указано количество деревьев, реконструированных по jackknife-репликам, в составе которых они были выявлены (фрагмент выдачи программы fconsense).|
|
Рис.
2. Ветви, входящие в состав деревьев, реконструированных по jackknife-репликам мутантных последовательностей гена glmS (фрагмент выдачи программы fconsense).
С помощью программы freetree пакета PHYLIP проведено укоренение дерева, реконструированного по методу NJ, в среднюю точку (см. результаты выполнения обязательных заданий). Были использованы следующие команды: ? (вызов справки о значении команд), M (Middle, укоренение в среднюю точку), F (Flip, поворот выбранного узла, в результате выполнения серии поворотов листья дерева были расположены в алфавитном порядке, что упростило сравнение топологии с топологией исходного дерева), W (Write, сохранение результата, при сохранении программа запросила, как следует сохранять результат: в виде укорененного или неукорененного дерева) и X (eXit, выход из программы). Скобочная формула полученного дерева приведена здесь.
Данный способ укоренения корректен, так как для рассмотренных последовательностей справедлива гипотеза "молекулярных часов" (исходное дерево является ультраметрическим). Это подтверждается тем, что топология NJ-дерева, укорененного в среднюю точку, совпадает с топологией исходного дерева (корень пришелся на ветвь, соединяющую точки расхождения последовательностей A, B, C и D, E, F). При работе с реальными последовательностями, особенно достаточно удаленными друг от друга, гипотеза "молекулярных часов", как правило, неприменима, в связи с чем необходимо использовать другие методы укоренения (например, укоренение путем включения в выборку эволюционно удаленного организма).
Построенное дерево было визуализировано с помощью программы fdrawgram. Информация о значении параметров программы была получена путем перенаправления потоков stdout и stderr при запуске с параметром help в текстовый файл):
fdrawgram -help 2> fdrawgram.txt
Программа fdrawgram визуализирует все деревья как укорененные (в отличие от fdrawtree, которая визуализирует все деревья как неукорененные, см. результаты выполнения обязательных заданий). Визуализация укорененного в среднюю точку NJ-дерева, построенная с помощью fdrawgram, приведена на рис. 3. Ниже приведена команда Linux, с помощью которой была запущена программа:
fdrawgram formula.txt tree.ps -style p -auto
Параметр style задает тип дерева (значение p соответствует филограмме - дереву с ветвями, расположенными параллельно друг другу).

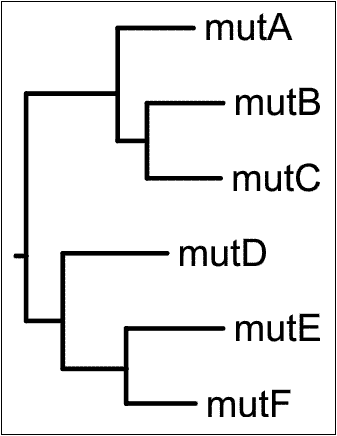
Рис.
3. Визуализация дерева, реконструированного по методу NJ и укорененного в среднюю точку. Обозначены листья (mutA-mutF). Длины ветвей пропорциональны эволюционным расстояниям. Визуализация построена с помощью программы fdrawgram.
Восстановление последовательности гена glmS по мутантным последовательностям (A-F) было проведено с помощью программы fdnamlk пакета PHYLIP. Данная программа предназначена для реконструкции деревьев методом максимального правдоподобия (ML) при условии выполнения гипотезы "молекулярных часов". Полученные деревья являются ультраметрическими и, следовательно, укорененными. Программа fdnamlk также позволяет осуществлять восстановление предковых последовательностей (соответствующих корню дерева). Восстановление позиций предковых последовательностей проводится на основе вычисленных для них значений параметра likelihood (правдоподобие), которые характеризует вероятность нахождения на каждого из нуклеотидов на данной позиции. Возможны следующие варианты:
Значение параметра likelihood некоторого нуклеотида превышает 0.50. В этом случае данный нуклеотид будет помещен на рассматриваемую позицию предковой последовательности (если likelihood > 0.95 — показан прописной буквой).
Значение параметра likelihood для каждого из нуклеотидов не превышает 0.50. В этом случае выбирается минимальное количество нуклеотидов (в порядке уменьшения likelihood), суммарное значение параметров likelihood для которых превышает 0.50. В соответствие с выбранными нуклеотидами на рассматриваемую позицию предковой последовательности помещается один из символов r, y, m и т.п. (по данным документации к программе dnamlk).
Запуск программы fdnamlk с целью восстановления предковой последовательности был проведен следующей командой Linux:
fdnamlk mutant.fasta -ttratio 0.5 -hypstate -auto
В связи с равновероятностью замен отношение частот транзиций и трансверсий (значение параметра ttratio) было принято равным 0.5 (см. результаты выполнения обязательных заданий). Параметр hypstate указывает на то, что помимо реконструкции дерева программа должна осуществить восстановление предковой последовательности.
Топология реконструированного дерева (рис. 4) совпадает с топологией исходного дерева. Расстояние между реконструированным и исходным деревьями, вычисленное согласно методике (см. результаты выполнения обязательных заданий), составляет 14.07, что ниже соответствующего значения для метода ML без условия выполнения гипотезы "молекулярных часов" (36.00) и близко к значению для метода UPGMA (12.38). Возможно, высокое сходство дерева, реконструированного с помощью программы fdnamlk, с исходным деревом связано с тем, что, помимо матриц расстояний, программа fdnamlk использует дополнительное предположение о справедливости гипотезы "молекулярных часов". Таким образом, при реконструкции дерева программа fdnamlk руководствуется большим количеством исходных данных, чем программа fdnaml.
Реконструированная предковая последовательность была сопоставлена с исходной последовательностью (последовательностью гена glmS) c использованием редактора выравниваний GeneDoc. Около половины позиций реконструированной последовательности содержат символы отдельных нуклеотидов (a, g, c, t). Остальные позиции содержат символы, обозначающие сразу несколько нуклеотидов (например, r, y и m, см. статистический отчет). Количество попарных различий между исходной последовательностью и ее реконструкцией составляет 71 на 100 н.п. (см. выравнивание) и приближается к количеству попарных различий, вычисленного для двух случайных последовательностей (75 на 100 н.п.). Таким образом, реконструированная предковая последовательность существенно отличается от исходной. Отличия могут быть обусловлены значительным эволюционным расстоянием между последовательностями листьев (A-F) и последовательностью, находящейся в корне дерева (240 замен на 100 н.п., то есть каждая позиция исходной последовательности в среднем мутировала более двух раз). Как было показано при выполнении обязательных заданий (работа с программой fdnadist), при таких расстояниях эволюционные модели начинают давать существенные сбои в связи с увеличением значимости вклада случайных отклонений. Следовательно, лучшие результаты могли бы быть получены либо при меньших эволюционных расстояниях между последовательностями, либо при работе с более объемной выборкой.
|
|
Рис.
4. Визуализация дерева, построенного с помощью программы fdnamlk.
© Куравский Михаил Львович, 2007