Главная страница > Четвертый семестр > Филогенетическое дерево и его реконструкция
Рассмотрено дерево, заданное скобочной формулой
((А:60,(В:50,С:50):10):60,(D:80,(Е:60,F:60):20):40);
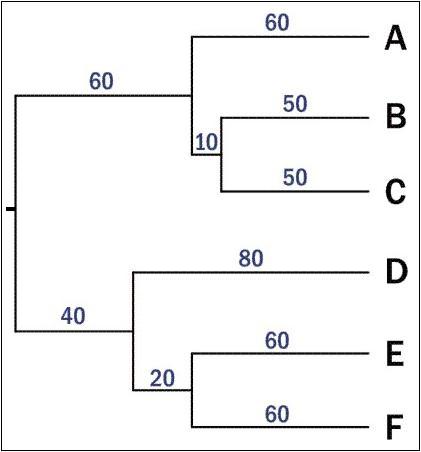
Данная скобочная формула содержит информацию о корне дерева, который расположен между точками расхождения последовательностей A, B, C и D, E, F. Дерево включает в себя шесть листьев, равноудаленных от корня дерева (суммы длин ветвей, соединяющих корень с каждым из листьев, равны друг другу и составляют 120 замен на 100 н.п.). Вероятно, для рассматриваемых последовательностей справедлива гипотеза "молекулярных часов": скорость накопления мутаций постоянна. Дерево было визуализировано средствами Corel Graphics Suite (рис. 1). Описание топологии дерева приведено в табл. 1.

Рис. 1. Визуализация дерева, заданного скобочной формулой (см. в тексте). Обозначены листья (A-F) и эволюционные расстояния (синим шрифтом). Длины ветвей пропорциональны эволюционным расстояниям.
Табл. 1. Описание топологии дерева, заданного скобочной
формулой (см. в тексте) как
разбиений множества листьев.
Ветви, отделяющие один лист от остальных, не показаны.
| A | B | C | D | E | F |
| . | * | * | . | . | . |
| . | . | . | * | * | * |
| . | . | . | . | * | * |
С помощью программы msbar* пакета EMBOSS была создана модель эволюции гена глюкозамин-6-фосфатсинтазы (glmS) E.coli. Данная последовательность рассматривалась как исходная (находящаяся в корне дерева). Считалось, что в ходе эволюции имеют место только замены нуклеотидов (в реальных биологических системах частоты других типов мутаций, таких как вставки, делеции, дупликации, инверсии, как правило, значительно меньше частоты замен). Расчет количеств замен (N), которые необходимо ввести в последовательность гена glmS, проводился в соответствии со следующей формулой:
N = 1.33 D L / 100 ,
где D — количество замен на 100 н.п., L = 1830 — длина гена glmS.
Коэффициент 1.33 был введен в связи с тем, что при генерации мутантных последовательностей программа msbar осуществляет замены нуклеотидов на один из четырех возможных вариантов (с равной вероятностью). Например, нуклеотид A может быть заменен не только на G, C или T, но и на A с той же вероятностью. Следовательно, значение параметра count (общее количество вносимых замен) в 4/3 раза превышает количество замен, приводящих к изменению нуклеотидного состава последовательности. Таким образом, для введения в последовательность n замен необходимо задать значение параметра count равным 4/3 n (приблизительно 1.33 n). Подробнее об этом см. результаты выполнения задания "Элементарные эволюционные события". Текст скрипта Linux, создающего файл, содержащий мутантные варианты последовательности гена glmS (позиции последовательностей, по которым произошли замены, показаны прописными буквами), приведен здесь. Полученным последовательностям были присвоены имена mutA - mutF в соответствии с листьями A-F исходного дерева.
Вычисление эволюционных расстояний между полученными мутантными последовательностями проведено с помощью программы fdnadist** пакета PHYLIP. Для оценки эволюционных расстояний использовалась модель Джукса-Кантора, которая исчерпывающе описывает работу программы msbar (при значении параметра point равному 4; подробнее см. результаты выполнения задания "Элементарные эволюционные события"). При работе с реально существующими последовательностями целосообразно использовать более сложную модель, например, модель Кимуры, которая позволяет учесть различия между частотами транзиций и трансверсий (Kimura, 1980; см. также руководство к пакету MEGA). По умолчанию fdnadist использует именно этот метод, причем отношение частот транзиций и трансверсий задается параметром ttratio. Однако, в модели эволюции, построенной с помощью программы msbar на основе последовательности гена glmS, частота транзиций в два раза меньше частоты трансверсий, т.е. все замены равновероятны (при использовании модели Кимуры следует задать параметр ttratio равным 0.5). Таким образом, при решении данной задачи метод Кимуры вырождается в метод Джукса-Кантора. Вследствие этого результаты выполнения следующих команд Linux совпадают:
fdnadist
mutant.fasta -method j -auto
fdnadist mutant.fasta -ttratio 0.5 -auto
Файл mutant.fasta, поданный на вход программы fdnadist, содержит множественное выравнивание анализируемых последовательностей, которое, в данном случае, совпадает с содержимым файла, созданного скриптом (см. выше). Это связано с тем, что в ходе "эволюции" имели место только замены нуклеотидов. Матрицы расстояний, полученные в результате выполнения обеих команд, совпадают (приведены здесь). Следует отметить, что в матрице расстояний расстояния приведены в среднем количестве замен, приходящемся на 1 н.п (а не на 100 н.п.). Вычисленные с помощью fdnadist расстояния в целом соответствуют истинным эволюционным расстояниям, заданным скобочной формулой дерева. Наибольшие различия (до 33 замен на 100 н.п.) свойственны наиболее удаленным друг от друга последовательностям (например, mutA и mutD). Появление таких различий связано с очень большим удалением последовательностей друг от друга (до 240 замен на 100 н.п., то есть каждая позиция мутировала в среднем более двух раз, и количество попарных различий приближается к максимальному — 75%). При этих условиях незначительные вариации количества попарных различий, обусловленные случайными причинами, приводят к значительно большим отклонениям эволюционных расстояний, вычисляемых по методу Джукса-Кантора.
На основе матрицы эволюционных расстояний, построенной с помощью программы fdnadist, были реконструированы деревья, описывающие предполагаемый ход эволюции последовательности glmS. Реконструкция деревьев проведена с помощью программы fneighbor пакета PHYLIP; использовались алгоритмы UPGMA (Unweighted Pair Group Method with Arithmatic mean) и NJ (Neighbor Joining). Кроме того, с помощью программы fdnaml того же пакета было реконструировано дерево по методу ML (Maximum Likelihood). Алгоритм данной программы, в отличие от fneighbor, не требует предварительной оценки эволюционных расстояний между анализируемыми последовательностями (на вход программы подается множественное выравнивание, как и при работе с fdnadist). Отношение частот транзиций и трансверсий (значение параметра ttratio) было принято равным 0.5 (см. выше).
При использовании каждого из методов реконструкции деревьев программой fneighbor были созданы по два файла: файл с расширением fneighbor и файл с расширением treefile. Первый из них содержит информацию о длинах ветвей реконструированного дерева (в виде таблицы), а также визуализацию дерева в текстовом виде (см. файлы с расширением fneighbor, созданные при использовании алгоритмов UPGMA и NJ). Файл с расширением treefile содержит скобочную структуру реконструированного дерева.
Программой fdnaml были созданы два файла, имеющие расширения fdnaml и treefile. Последний, как и в случае fneighbor, содержит скобочную формулу реконструированного дерева. Файл с расширением fdnaml, помимо визуализации дерева и длин ветвей, содержит доверительные интервалы для длин ветвей (подробнее см. ниже), информацию о частотах встречаемости различных типов нуклеотидов в анализируемых последовательностях, а также отношение количеств транзиций и трансверсий, совпадающее с предполагаемым значением (отношением их частот, заданным как значение параметра ttratio).
Полученные скобочные формулы деревьев, а также команды Linux, с помощью которых были запущены программы, приведены в табл. 2.
* Подробнее о работе программы msbar см. результаты выполнения задания "Элементарные эволюционные события".
** Информация о значении параметров программ fdnadist, fneighbor и fdnaml получена путем перенаправления потоков stdout и stderr при запуске с параметром h в текстовые файлы.
Табл. 2. Команды
Linux,
с помощью которых были запущены программы, осуществляющие реконструкцию
деревьев различными методами, и скобочные формулы полученных деревьев.
| Название метода | Команда Linux | Скобочная формула реконструированного дерева |
| UPGMA | fneighbor mutant.fdnadist -treetype u -auto | ((mutA:0.60770,(mutB:0.50552,mutC:0.50552):0.10218):0.59146,(mutD:0.84670,(mutE:0.56097,mutF:0.56097):0.28573):0.35246); |
| NJ | fneighbor mutant.fdnadist -treetype n -auto | ((mutB:0.51403,mutC:0.49702):0.19753,(mutD:0.70492,(mutE:0.65450, mutF:0.46744):0.42751):0.86487,mutA:0.51235); |
| ML | fdnaml mutant.fasta -ttratio 0.5 -auto |
(((mutF:0.40775,mutE:0.71276):0.40105,mutD:0.71304):0.87285, (mutB:0.49728,mutC:0.51461):0.19309,mutA:0.51682); |
Реконструированные деревья были визуализированы с помощью программ drawgram и drawtree пакета PHYLIP (использовались online-версии программ, доступные на сайте Пастеровского Института). Скобочная формула дерева, построенного по методу UPGMA, содержит информацию о расположении корня дерева (в отличие от скобочных формул деревьев, реконструированных методами NJ и ML). При этом данный метод действительно позволяет установить расположение корня дерева, а не помещает его случайным образом (подробное описание алгоритма UPGMA см. результаты выполнение задания "Филогенетические деревья, реконструированные разными способами" за второй семестр). Поэтому для визуализации дерева, реконструированного методом UPGMA, была применена программа drawgram, которая строит укорененные деревья (рис. 2А). Соответственно, для визуализации деревьев, реконструированных методами NJ и ML, была применена программа drawtree, строящая неукорененные деревья (рис. 2 Б, В).
Топология всех трех деревьев совпадает и соответствует исходному сценарию эволюции. Описание топологии деревьев как разбиений множества листьев приведено в табл. 3. Близость результатов, полученных разными методами, свидетельствует об их корректности, что и подтверждается сходством с исходным деревом.
Для сравнения деревьев, реконструированных тремя различными методами, с деревом, описывающим истинный сценарий эволюции, каждое из них было представлено в виде вектора многомерного пространства, координаты которого соответствуют длинам ветвей. В связи с тем, что с помощью методов NJ и ML были получены неукорененные деревья, исходное дерево и дерево, реконструированные по методу UPGMA, были также приведены к неукорененному виду: длина ветви, соединяющей точку расхождения последовательностей A, B и C с точкой расхождения последовательностей D, E и F, была вычислена как сумма расстояний от данных точек до корня дерева. В качестве оценки степени различия реконструированных деревьев и исходного дерева использовалось расстояние между соответствующими векторами, вычисленное в евклидовой метрике (корень из суммы квадратов разностей координат). Применение данного способа оценки справедливо, так как (1) топология всех деревьев совпадает, и (2) длины ветвей выражены в одних и тех же единицах измерения (количество замен на 100 н.п.). Вычисления были проведены с помощью электронной таблицы Excel.
Как показали результаты вычислений, ближе всего к исходному дереву располагается дерево, реконструированное по методу UPGMA (расстояние составляет 12.38). Расстояния между исходным деревом и деревьями, реконструированными по методам NJ и ML, значительно выше (33.47 и 36.00 соответственно).
Алгоритм UPGMA реконструирует ход эволюции в предположении о справедливости гипотезы "молекулярных часов" (скорость накопления мутаций поcтоянна, см. Kimura and Ohta, 1968). Вследствие этого суммарные расстояния от корня дерева до каждого из его листьев оказываются равны друг другу (см. рис. 2 А). При анализе реальных последовательностей гипотеза "молекулярных часов" имеет свою область применимости. Например, в работе Tajima (1993) было показано, что данная гипотеза неверна для последовательностей митохондриальных ДНК гоминид. Как правило, гипотеза "молекулярных часов" неприменима для достаточно удаленных друг от друга последовательностей. Узкая область применимости гипотезы "молекулярных часов" ограничивает использование метода UPGMA на практике (см. сайт Norwegian Functional Genomics Program).
Однако в рассмотренной модели эволюции скорости накопления мутаций постоянны и не зависят от ветви дерева, на которой расположена последовательность (то есть расстояния от корня исходного дерева до каждого из его листьев равны). В связи с этим дерево, реконструированное по методу UPGMA, неплохо согласуется с истинным ходом "эволюции". Так, вычисленные по данному методу длины ветвей практически совпадают с длинами ветвей исходного дерева, и максимальное отклонение не превышают 8 замен на 100 н.п. Возможно, более высокое сходство дерева, реконструированного по методу UPGMA, с исходным деревом связано с тем, что, помимо матриц расстояний, данный алгоритм использует дополнительное предположение о справедливости гипотезы "молекулярных часов". Таким образом, при построении дерева алгоритм UPGMA руководствуется большим количеством исходных данных. В выборках реальных последовательностей скорость накопления мутаций, как правило, не является постоянной, что может стать причиной ошибок при реконструкции деревьев методом UPGMA. В этих случаях для реконструкции деревьев следует использовать методы NJ или ML.
Методы NJ и ML учитывают различия в скорости накопления мутаций в разных последовательностях. Это дает определенные преимущества при анализе выборок реальных последовательностей. Однако, для рассмотренной модели эволюции имеют место значительные расхождения между истинными эволюционными расстояниями и их оценками. Например, истинные расстояния от точки расхождения последовательностей E и F равны 60, метод NJ оценил их равными 65 и 47 соответственно, а метод ML - 71 и 41 соответственно. Алгоритм ML, в отличие от NJ, позволил оценить доверительные интервалы длин ветвей уровня значимости 0.01 (см. файл с расширением fdnaml).
Следует отметить, что метод NJ справился с реконструкцией дерева значительно быстрее, чем метод ML. Для выборки из шести последовательностей различия во времени работы составляют секунды, однако для выборок реально существующих последовательностей большего объема, особенно при проведении бутстреп-анализа (см. ниже), различия по времени работы могут оказать влияние на выбор алгоритма.
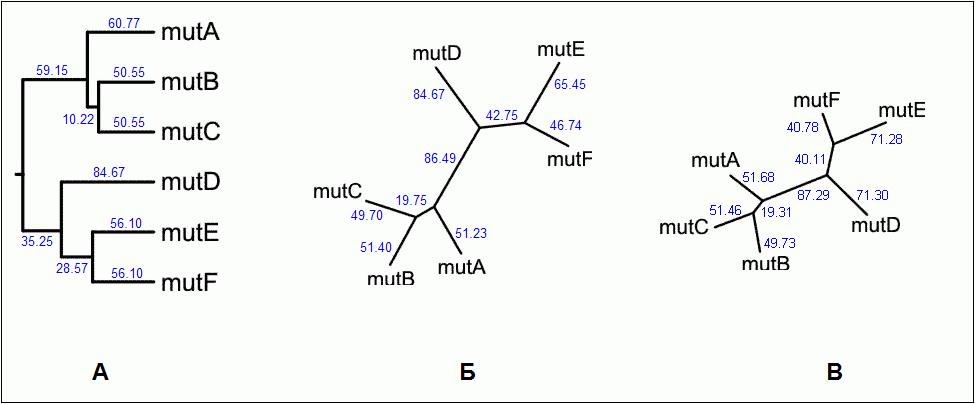
Рис. 2 (А, Б, В). Деревья, реконструированные методами UPGMA (А), NJ (Б) и ML (В). Скобочные формулы были визуализированы с помощью программ drawgram (А) и drawtree (Б, В) пакета PHYLIP. Длины ветвей соответствуют количеству замен на 100 н.п.
Табл. 3. Описание топологии
исходного дерева и деревьев, реконструированных тремя различными методами, как
разбиений множества листьев.
Ветви, отделяющие один лист от всех остальных, не показаны.
| Листья | Входит ли в состав дерева, построенного с использованием данного алгоритма? | ||||||||
| A | B | C | D | E | F | исходное | UPGMA | NJ | ML |
| . | * | * | . | . | . | + | + | + | + |
| . | . | . | * | * | * | + | + | + | + |
| . | . | . | . | * | * | + | + | + | + |
Для оценки статистической надежности ветвей реконструированных деревьев был проведен бутстреп-анализ выравнивания мутантных последовательностей. С помощью программы fseqboot пакета PHYLIP были созданы 100 бутстреп-реплик данного выравнивания. Команда Linux, с помощью которой была запущена программа, приведена ниже:
fseqboot mutant.fasta -auto
Помимо бутстреп-реплик множественных выравниваний программа fseqboot способна создавать реплики, используя такие методы, как delete-half-jackknifing* и permuting species within characters. Для выбора метода необходимо задать соответствующее значение параметра test: значение b для выбора выбора метода bootstrapping, j — delete-half-jackknifing и с — permuting species within characters. Подробнее о методах jackknifing и их отличиях от метода bootstrapping см. результаты выполнения дополнительных заданий. Метод permuting species within characters отличается от двух других методов по своему предназначению: он служит не для оценки статистической надежности топологии реконструированного дерева, а для проверки гипотезы об отсутствии таксономической структуры в исходной выборке. При запуске со значением параметра test, равным с, программа fseqboot случайным образом осуществляет перестановку символов в пределах столбцов исходного множественного выравнивания. Если в полученных таким способом репликах эволюционные расстояния между двумя последовательностями будут значительно превышать эволюционное расстояние, вычисленное по исходному выравниванию, то можно утверждать, что рассматриваемые последовательности являются родственными (по данным документации к программе fseqboot).
В результате выполнения программы fseqboot был создан файл с расширением fseqboot, содержащий полученные бутстреп-реплики. Каждая реплика представляет собой множественное выравнивание в формате PHYLIP (в верхней строке указано количество последовательностей в выравнивании и длина выравнивания, ниже расположено само выравнивание). Таким образом, получив на вход выравнивание в формате fasta, которое не может быть корректно обработано программами некоторых версий пакета PHYLIP (не инкорпорированных в EMBOSS), fseqboot выдала реплики в другом формате, пригодном для дальнейшего анализа любыми версиями программ пакета PHYLIP. Это может помочь избежать затрат времени на преобразования реплик из одного формата в другой (например, если дальнейший анализ полученных реплик производится на другом компьютере). Помимо формата fasta программа fseqboot способна обрабатывать исходные выравнивания и в других форматах, например, в формате Clustal (который, как и fasta, достаточно часто используется): при подаче на вход программы множественного выравнивания мутантных последовательностей, построенного с помощью программы ClustalW, fseqboot построила реплики, не выдав сообщения об ошибке. Таким образом, возможность анализа выравниваний последовательностей в различных форматах является одним из преимуществ версий программ пакета PHYLIP, инкорпорированных в EMBOSS.
С помощью программы fdnaml по методу ML были реконструированы деревья для каждой из реплик (отношение частот транзиций и трансверсий было принято равным 0.5, см. выше). Реконструкция деревьев для 100 реплик, включающих в себя по шесть последовательностей, заняла продолжительное время (несколько минут). Как правило, в научных исследованиях проводится реконструкция деревьев для значительно большего числа последовательностей. При этом оценка надежности топологии осуществляется путем построения не менее 1000 бутстреп-реплик (по данным molbiol.ru). В связи с этим использование более быстрых методов реконструкции деревьев (например NJ) является целесообразным, если не идет в ущерб качеству.
В результате выполнения программы fdnaml были созданы два файла, имеющие расширения fdnaml и treefile (о характере информации, хранящейся в этих файлах, см. выше). Скобочные формулы 100 реконструированных по репликам деревьев, содержащиеся в файле с расширением treefile, были проанализированы с помощью программы fconsense. Команда Linux, с помощью которой была запущена данная программа, приведена ниже:
fconsense mutant.treefile -auto
Программа fconsense осуществляет реконструкцию консенсусных деревьев с помощью одного из четырех возможных методов: minimum fraction, majority rule, extended majority rule и strict. Используемый метод задается параметром программы method. Наиболее общим является метод minimum fraction, при применении которого программа включает в состав консенсусного дерева только те ветви, которые присутствуют более чем в заданном количестве реплик. Пороговое количество реплик не может превышать 1/2 от их общего количества. Это связано с тем, что те ветви, которые присутствуют в составе более чем половины деревьев, реконструированных по репликам, заведомо совместимы друг с другом, чего нельзя сказать о ветвях, входящих в состав менее чем половины деревьев. Пороговое значение количества реплик задается параметром mlfrac, который, соответственно, может принимать значения от 0.5 до 1.0. Методы majority rule и strict являются частными случаями метода minimum fraction: для первого из них значение параметра mlfrac принято равным 0.5, для второго — 1.0. Метод extended majority rule, используемый программой fconsense по умолчанию**, сначала включает в состав консенсусного дерева те ветви, которые присутствуют более чем в половине реконструированных по репликам деревьев (как и метод majority rule), а затем в порядке встречаемости добавляет оставшиеся ветви, которые совместимы с уже включенными (по данным документации к программе consense).
В качестве критерия для оценки статистической надежности ветвей консенсусного дерева было выбрано пороговое значение в 50 деревьев (надежными считались те ветви, которые входят в состав более чем половины деревьев, реконструированных по репликам: в состав консенсусного дерева, построенного методом extended majority rule, также могут входить ветви, присутствующие менее чем в половине деревьев). По результатам Berry and Gascuel (1996), оптимальное пороговое значение определяется количеством столбцов исходного выравнивания (при увеличении длины выравнивания уменьшается возможный вклад случайных ошибок, вследствие чего для более длинных выравниваний оптимальное пороговое значение выше, чем для более коротких) и, в меньшей степени, методом реконструкции деревьев по бутстреп-репликам (авторами данной статьи были рассмотрены методы maximum parsimony и один из distance methods, для первого оптимальные пороговые значения несколько ниже, чем для второго).
В результате выполнения программы fconsense был создан файл с расширением fconsense и обновлен исходный файл с расширением treefile***. Файл fconsense содержит список всех ветвей, присутствующих в деревьях, реконструированных по бутстреп-репликам (рис. 3). Ветви представлены в виде разбиений множества листьев (как в табл. 1 и 2). Указано количество деревьев, в составе которых были выявлены данные ветви, а также те ветви, которые включены в состав консенсусного дерева. Кроме того, приведена визуализация консенсусного дерева в текстовом виде (дерево неукорененное, так как реконструкция деревьев по репликам проводилась с помощью метода ML, позволяющего строить только неукорененные деревья, рис. 4). Обновленный файл с расширением treefile содержит скобочную формулу консенсусного дерева, в которой вместо длин ветвей указано количество деревьев в составе которых эти ветви были выявлены (длины ветвей, отделяющих один лист от всех остальных, составляют 100, так как такие ветви присутствуют в любом дереве, реконструированном для данных последовательностей).
Топология консенсусного дерева совпадает с топологией исходного дерева и топологией деревьев, реконструированных тремя различными методами. При этом для каждой из внутренних ветвей количество деревьев, в которых эта ветвь присутствовала, близко к 100 (88, 97 и 100) и значительно превышает выбранный критерий (50). Ветви, не вошедшие в состав консенсусного дерева, были выявлены в значительно меньшем количестве деревьев (не более 9). Таким образом, топология реконструированных деревьев являются достаточно надежной.
Следует отметить, что количество деревьев, в которых присутствовали внутренние ветви консенсусного (и исходного) деревьев, коррелирует с длинами этих ветвей. Так, длина ветви исходного дерева, соединяющей точку расхождения последовательностей A, B и C с точкой расхождения последовательностей B и C составляет 10 замен на 100 н.п., эта ветвь была выявлена в 88 деревьях из 100. Длина ветви, соединяющей точку расхождения последовательностей D, E и F с точкой расхождения последовательностей E и F составляет 20 замен на 100 н.п., и эта ветвь была выявлена уже в 97 деревьях из 100. Ветвь, соединяющая точку расхождения последовательностей A, B и C с точкой расхождения последовательностей D, E и F имеет длину 100 замен на 100 н.п. и присутствовала во всех деревьях, реконструированных по бутстреп-репликам. Возможно это связано с тем, что при небольших эволюционных расстояниях и небольших объемах выборок (при построении реплик по методу bootstrapping теряется половина информации исходного множественного выравнивания) повышается вероятность того, что по случайным причинам эволюционно более отдаленные последовательности внутри некоторых реплик окажутся более сходными друг с другом, чем последовательности, эволюционно более близкие друг к другу. При этом такие ложные ветви (которые не вошли в состав консенсусного дерева в связи с тем, что они несовместимы с более часто встречающимися истинными ветвями) в основном должны имеют небольшую длину. Это согласуется с выдачей программы fdnaml. Например, в дереве, реконструированном по 12-й реплике, длина ложной ветви, соединяющей точку расхождения последовательностей A и B и точку расхождения всех остальных последовательностей составляет приблизительно 4 замены на 100 н.п.
* Также существует метод delete-fraction-jackknifing, который осуществляет удаление e-1 столбцов выравнивания.
** При заданном параметре auto.
*** Имя выходных файлов было задано по умолчанию, т.е. совпадающим с именем исходного файла.
|
|
Рис. 3.
Ветви, входящие в состав деревьев, реконструированных по бутстреп-репликам мутантных последовательностей гена glmS (фрагмент выдачи программы fconsense).|
|
Рис. 4.
Визуализация консенсусного дерева. Для внутренних ветвей указано количество деревьев, реконструированных по бутстреп-репликам, в составе которых они были выявлены (фрагмент выдачи программы fconsense).
Исходное дерево было визуализировано с помощью программы fdrawtree пакета PHYLIP (использовалась версия пакета, инкорпорированная в EMBOSS; о работе с online-версией программы drawtree на сайте Пастеровского института см. выше). Информация о значении параметров программы была получена с помощью следующей команды Linux (проведено перенаправление потоков stdout и stderr при запуске с параметром help в текстовый файл):
fdrawtree -help 2> fdrawtree.txt
Данная программа визуализирует все деревья как неукорененные (в отличие от fdrawgram, которая визуализирует все деревья как укорененные, см. результаты выполнения дополнительных заданий). С параметрами, заданными по умолчанию, программа выдает графический файл в формате postscript; длины ветвей дерева пропорциональны эволюционным расстояниям. Визуализация исходного дерева, построенная с помощью fdrawtree, приведена на рис. 5. Ниже приведена команда Linux, с помощью которой была запущена данная программа:
fdrawtree
formula.txt tree.ps -auto
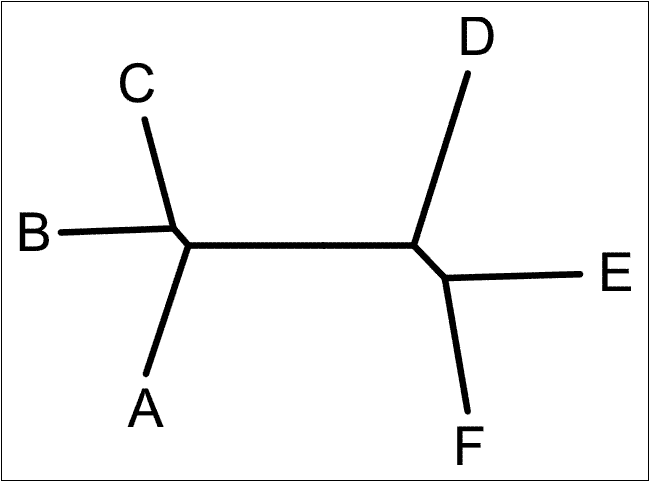
Рис. 5. Визуализация дерева, заданного скобочной формулой. Обозначены листья (A-F). Длины ветвей пропорциональны эволюционным расстояниям. Визуализация построена с помощью программы fdrawtree.
© Куравский Михаил Львович, 2007