Алгоритмы и программы множественного выравнивания
Задание 2. Сравнивание выравниваний разных программ
Для множественного выравнивания среди белков, имеющих доменную архитектуру:
Cas3_HD - DEAD - Cas3-like_C_2 - Cas3_C
Я выбрал десять случайных последовательностей:
-A1ARI0 из Pelobacter propionicus
-A4XYU5 из Ectopseudomonas mendocina
-A8M400 из Salinispora arenicola
-A8SDS1 из Faecalibacterium prausnitzii
-B1VIY4 из Corynebacterium urealyticum
-B5GA96 из Streptomyces sp.
-B6XT60 из Bifidobacterium catenulatum
-C1DSH5 из Azotobacter vinelandii
-C2BEU2 из Anaerococcus lactolyticus
-C3PF92 из Corynebacterium aurimucosum
-и ещё одну репрезентативную последовательность Q5YRB2 из Nocardia farcinica
Затем в приложении Jalview провёл три выравнивания при помощи программ множественного выравнивания Mafft, Muscle и Clustal.
Для того, чтобы сравнить выравнивания я использовал программу Куликова Антона MSA.py (Ссылка на 13-ый практикум Куликова Антона)
Я решил сравнить выравнивания, построенные программой Muscle с выравниваниями, построенными программами Mafft и Clustal: Проект Jalview
Текстовая выдача программы MSA.py при сравнении выравниваний, сделанных программами Muscle и Mafft
Текстовая выдача программы MSA.py при сравнении выравниваний, сделанных программами Muscle и Clustal
| Первая программа | Вторая программа | Длина выравнивания и процент совпадающих колонок первого выравнивания | Длина выравнивания и процент совпадающих колонок второго выравнивания | Координаты совпадающих блоков | Координаты совпадающих индивидуальных колонок |
|---|---|---|---|---|---|
| Muscle | Mafft |
1228 51.55% |
1265 50.04% |
21-22 = 23-24 39-52 = 42-55 92-93 = 95-96 111-127 = 114-130 167-178 = 189-200 198-213 = 220-235 244-261 = 265-282 265-273 = 286-294 283-298 = 304-319 302-304 = 323-325 387-463 = 414-490 470-473 = 497-500 483-491 = 510-518 522-524 = 552-554 528-623 = 558-653 637-657 = 672-692 674-675 = 709-710 682-697 = 717-732 718-723 = 753-758 727-759 = 762-794 764-772 = 799-807 777-778 = 812-813 782-785 = 817-820 791-818 = 826-853 820-823 = 855-858 827-828 = 862-863 830-877 = 865-912 929-941 = 963-975 944-945 = 978-979 948-970 = 982-1004 1051-1072 = 1096-1117 1102-1119 = 1145-1162 1151-1168 = 1193-1210 1178-1190 = 1220-1232 1194-1204 = 1236-1246 |
59=62 240=261 278=299 300=321 465=492 467=494 498=525 897=935 925=959 972=1006 1172=1214 1175=1217 |
| Clustal |
1228 38.11% |
1158 40.41% |
62-81 = 50-69 105-127 = 93-115 198-210 = 180-192 212-213 = 194-195 279-298 = 251-270 325-334 = 292-301 401-463 = 365-427 470-473 = 434-437 480-495 = 444-459 521-526 = 486-491 528-539 = 493-504 542-625 = 507-590 682-685 = 647-650 720-724 = 684-688 729-758 = 693-722 764-768 = 728-732 792-815 = 749-772 838-877 = 789-828 929-943 = 878-892 956-970 = 903-917 1059-1068 = 999-1008 1151-1169 = 1086-1104 1177-1190 = 1112-1125 1194-1204 = 1129-1139 |
498=462 1056=996 1171=1106 |
Надо учесть то, что под блоком в программе понимается не достоверный блок без гэпов, а блок, состоящий из несколько подряд идущих идентичных колонок в выравнивании.
Исходя из таблицы и из текстового вывода программы становится очевидным, что выравнивание алгоритмом Mafft в данном случае более близко к выравниванию алгоритмом Muscle (51.55% идентичности), нежели выравнивание алгоритмом Clustal к выравниванию алгоритмом Muscle(всего 38.11% идентичности).
Самые крупные идентичные блоки выравниваний Muscle и Mafft, имеющие длину 77 (387-463), 96 (528-623) и 48 (830-877), больше, чем самые крупные идентичные блоки выравниваний Muscle и Clustal, имеющие длину 63(401-463), 84(542-625) и 40(838-877). Что также говорит нам о бóльшей схожести алгоритмов Mafft и Muscle. Также интересно то, что эти блоки приурочены к доменам PF00270 (DEAD/DEAH box helicase domain) и PF22590 (Cas3-like_domain)
P.S. - в скобках идентичность и координаты даны относительно выравнивания алгоритмом Muscle.
Задание 3. Построение выравниваний по совмещению структур
Для выравнивания по совмещению 3D-структур я выбрал 3 белка из семейства PF01036 (Bacteriorhodopsin-like protein):
-S5DM51 из Candidatus Actinomarina minuta (граммположительный, актиномицет) с 3D-структурой 7avn (Structure of marine actinobacteria clade rhodopsin (MacR) in orange form in P1 space group)
-H9ZSC3 из Thermus thermophilus JL-18 (граммотрицательный экстремофил) с 3D-структурой 5azd (Crystal structure of thermophilic rhodopsin)
-P02945 из Halobacterium salinarum (архея) с 3D структурой 1ap9 (X-RAY STRUCTURE OF BACTERIORHODOPSIN FROM MICROCRYSTALS GROWN IN LIPIDIC CUBIC PHASES)
Для начала я загрузил я провёл выравнивание 3D-структур 1ap9 с 7avn и 1ap9 c 5azd. Затем я по методике в пояснении добавлял в необходимых местах гэпы, после чего удалил лишнюю последовательность и получил нужное выравнивание 3D-структур. Затем, используя внутренний сервис Mafft в другом окне провёл выравнивание.
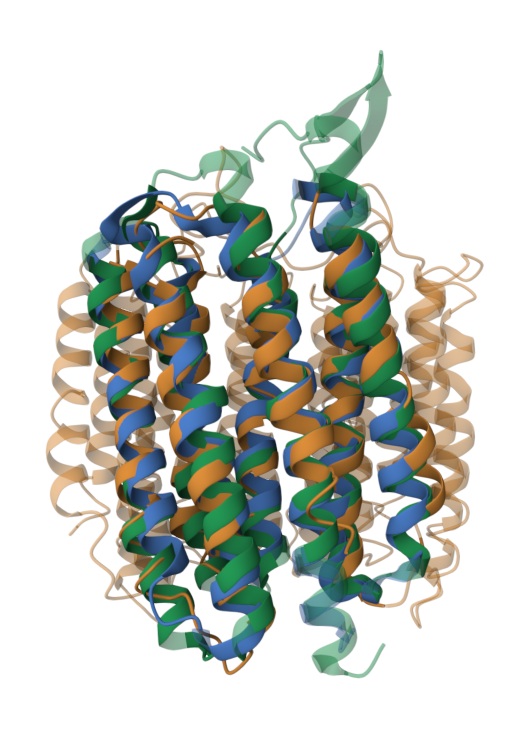
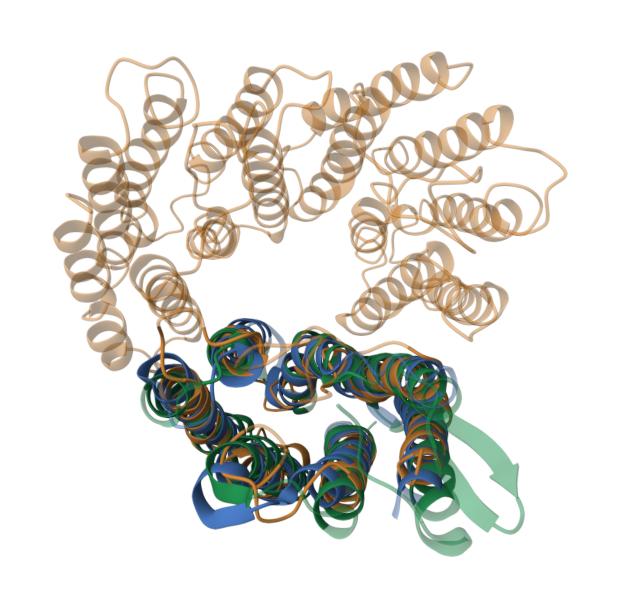
Проект Jalview с выравниванием 3D-структур и выравниванием алгоритмом Mafft.
Потом при помощи вышеупомянутой программы MSA.py от Куликова Антона сравнил два выравнивания (Текстовая выдача программы)
| Длина выравнивания и процент совпадающих колонок выравнивания 3D-структур | Длина выравнивания и процент совпадающих колонок выравнивания Mafft | Координаты совпадающих блоков | Координаты совпадающих индивидуальных колонок |
|---|---|---|---|
|
268 51.49% |
267 51.69% |
7-9 = 7-9 17-35 = 17-35 41-68 = 41-68 72-74 = 79-81 86-91 = 71-76 100-118 = 97-115 139-152 = 138-151 208-221 = 209-222 240-268 = 239-267 |
1=1 80=87 130=123 |
Задание 4. Описание программы Muscle
Выравнивания имеют почти что одинаковую длину, однако процент индентичности не столь большой (чуть больше 50%). Начальные участки выравнивания не совпадают, а конечные, наоборот, совпадают.
3D-структура в основном представлена альфа спиралями, которые соединены между собой петлями или бета-слоями. И по идее, выравнивание должно идти между альфа-спиралями, поскольку они составляют основу родопсина и нужны для выполнения функций, а потому аминокислотная последовательность в эти местах достаточно консервативная, и наоборот, выравнивания на участках с бета слоями и петяли не должно быть. Но при выравнивании программой Mafft на участке выравнивания 70-95, соответствующем петлям и бета-слоям, которые никак не сходятся по 3D-структуре, алгоритм выравнивает белки и находит даже консервативную позицию.
Задание 4. Описание программы ClustalW
Оригинальная программа Clustal была создана в 1988 году, в её основе лежало проведение парных выравниваний последовательностей (аминокислот или нуклеотидов) между собой для построение филогенетического древа, а после следовало выравнивание выравниваний, находящихся наиболее близко друг к другу [1]. Оценка сходства последовательностей вычислялась как кол-во совпадающих слов длины k (алгоритм Нидлмана-Вунша) между двумя последовательностями. Затем строилась матрица, где каждая точка соответствовала совпадениям слов. После алгоритм выбирал N лучших диагоналей и проводил поиск вокруг них. Затем выбирались слова длины k на лучших диагоналях и строилось выравнивание [2].
Программа Clustal учитывает эволюционную близость и больше доверяет выравниваниям близкородственных последовательностей. Для оценки расстояний между последовательностями используется формула:
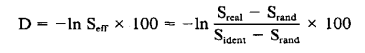
Где S(real) - вес выравнивания; S(rand) - вес выравнивания для случайных последовательностей той же длины и состава; S(ident) - средний вес двух последовательностей, если каждая из них будет выравниваться сама с собой [1].
Затем строится дерево, на основе расстояний между последовательностями, где листья дерева - это последовательности, а ветки, соединяющие листья - выравнивания (или кластеры). Построение выравниваний (кластеризация) идёт от листьев к стволу дерева, от наименьшего расстояния к наибольшему. Расстояние между выравниванием (кластером) и последовательностью/другим выравниванием (кластером) вычисляется как среднее расстояние между каждой последовательностью одного выравнивания (каждым элементом одного кластера) и другой последовательностью/каждой последовательностью другого выравнивания (каждым элементом другого кластера) [3].
Используемая литература
[1] Feng, D. F., & Doolittle, R. F. (1987). Progressive sequence alignment as a prerequisite to correct phylogenetic trees. Journal of molecular evolution, 25(4), 351–360. https://doi.org/10.1007/BF02603120
[2] DendroUPGMA 201410 – A Dendrogram Construction Utility
[3] Higgins, Des (June 1991). "Clustal V Multiple Sequence Alignments. Documentation (Installation and Usage)"