Восстановление электронной плотности
Модель
В качестве примера для восстановления электронной плотности была использована следующая модель: две линейных молекулы H-C-C-H и O-N-O расположены на отрезке [0;30] Å. Расстояние между молекулами - 5.5 Å, длина всех связей - 1.5 Å. Электронные плотности (ЭП) атомов описываются гауссовой кривой, максимум которой в центре атома приблизительно пропорционален числу электронов в атоме. Для этой модели была задана функция линейной электронной плотности с помощью модифицированного скрипта compile-func.py следующей командой:
compile-func.py -g 2,2,8+24,2,9.5+24,2,11+2,2,12.5+32,2,18+28,2,19.5+32,2,21
На выходе получили поточечные координаты функции ЭП и её график (см. рис.1).
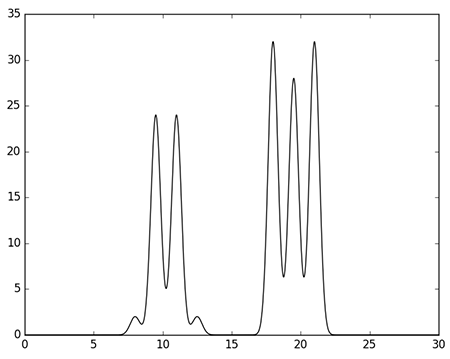
|
| Рис. 1. Одномерный график электронной плотности выбранной модели. |
Полные наборы гармоник
С помощью немного измененного скрипта func2fourier.py было получено преобразование Фурье функции ЭП с нулевым уровнем шума по фазе и амплитуде. Получили файл с набором из 499 гармоник и затем создали несколько аналогичных файлов, содержащих только первые 26, 20, 15 или 5 гармоник.
По полученным разложениям Фурье слегка модифицированным скриптом fourier2func.py востановили функцию ЭП и построили графики этих функций. Качество восстановленной функции получилось тем выше, чем больше гармоник использовалось. Для 499 гармоник (см. рис. 2) график не отличается от исходной функции.
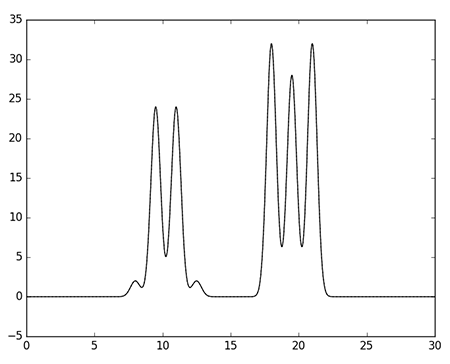
|
| Рис. 2. Восстановленная функция ЭП по набору изз 499 гармоник. Здесь и далее исходная функция показана сплошной линией, а восстановленная - пунктирной. |
Для 26 гармоник уже появляется много "лишних" пиков, но качество всё ещё остаётся отличным (см. рис. 3). Для меньшего числа гармоник качество уже ниже, чем отличное, поэтому число 26 было принято за n_0 - минимальное число гармоник, при котором качество остаётся отличным.
А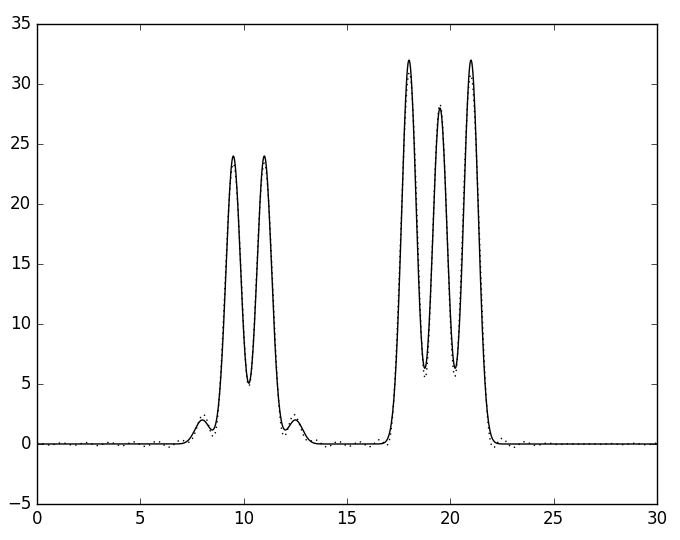
|
Б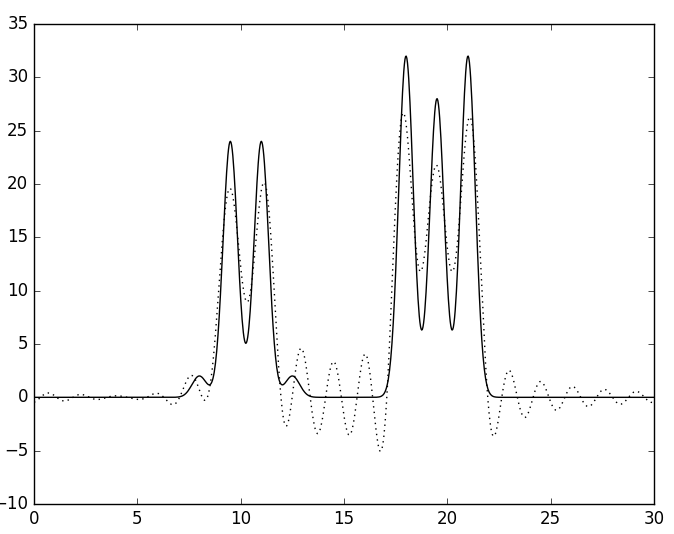
|
В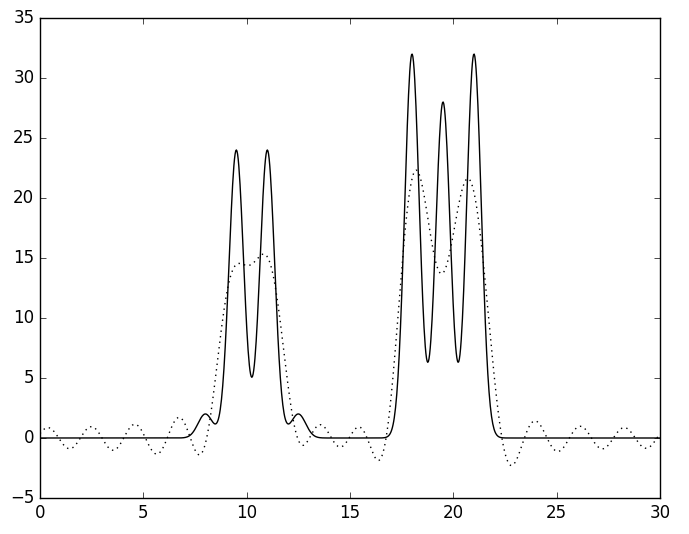
|
Г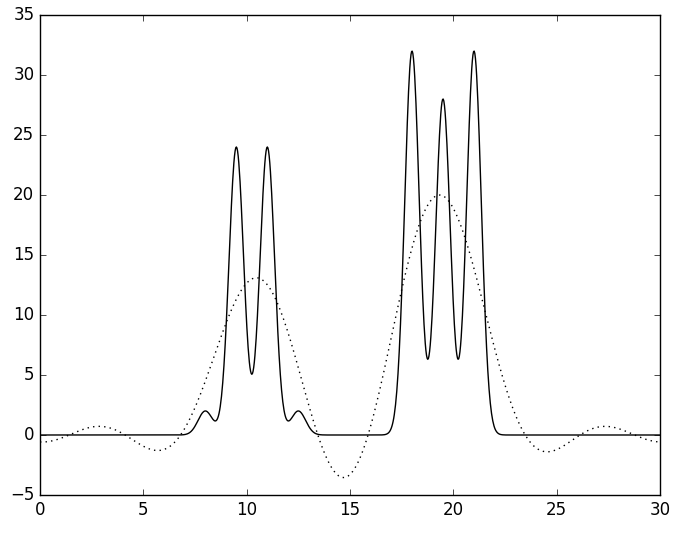
|
| Рис. 3. Восстановленная функция ЭП по набору из 26 (А), 15 (Б), 10 (Г) и 5 (Д) гармоник. | |
Однако, реальные данные всегда содержат шум, поэтому скриптом func2fourier.py были созданы разложения функции ЭП, содержащие разный процент шума по амплитуде и/или фазе и включающие в себя полный набор из 26 гармоник. Сначала одинаковй процент шума добавляли и по фазе, и по амплитуде - 20, 10 и 5 процентов (см. рис. 5). Качество восстановления функции ЭП можно назвать хорошим только при 5 процентах шума. Стоит отметить, что эти результаты в некоторой степени случайны, так как шум добавляется случайным образом, а мы смотрим только по 1 из возможных картинок.
А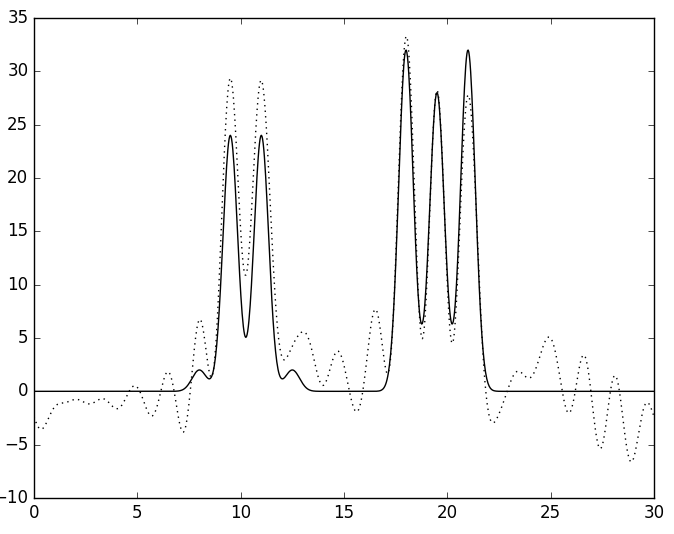
|
Б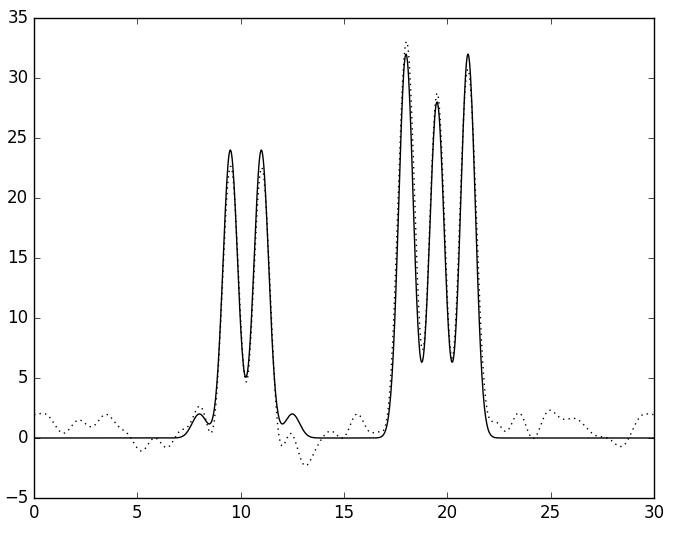
|
В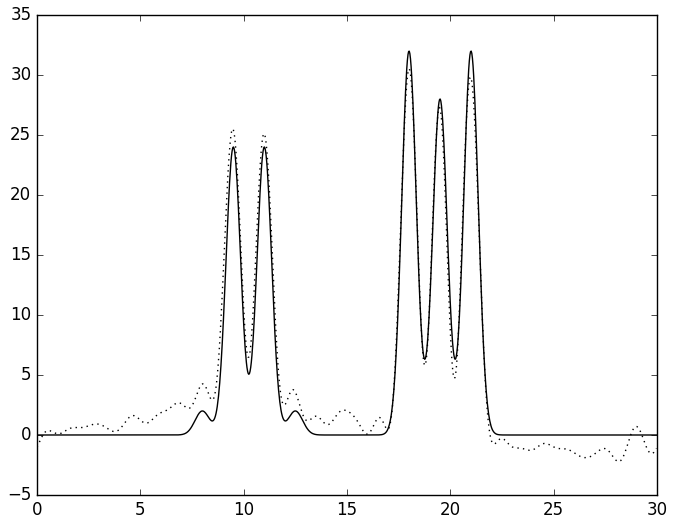
|
| Рис. 5. Восстановленная функция ЭП по полному набору гармоник с шумом по фазе и амплитуде в 20 (А), 10 (Б) и 5 (В) процентов. | ||
Затем шум добавляли отдельно по фазе и по амплитуде. На рисунке 6 приведены восстановленные функции ЭП по наборам гармоник с шумом в 20 и 40% по амплитуде. Шум сильно снизил качество восстановления, при 20% оно хорошее, ари 40 - среднее.
А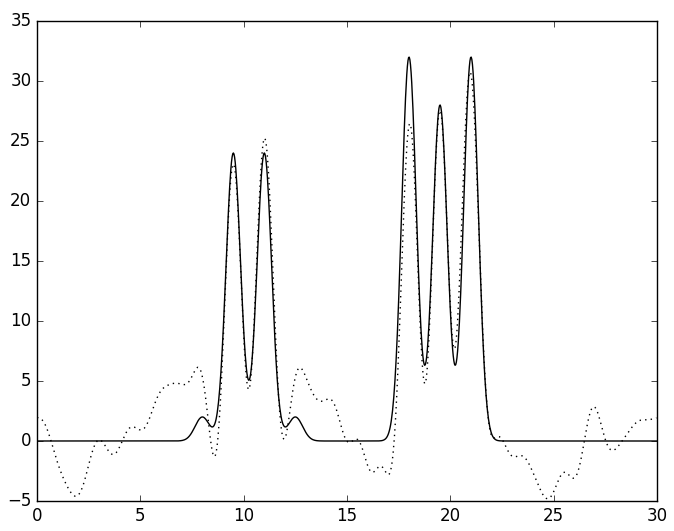
|
Б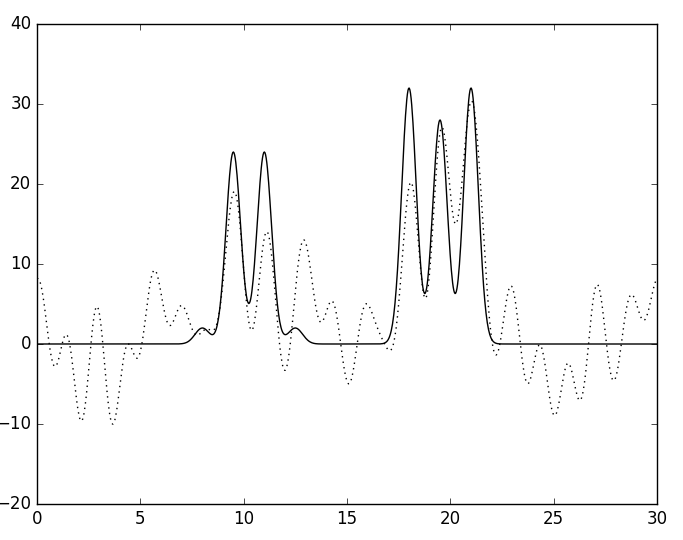
|
| Рис. 6. Восстановленная функция ЭП по полному набору гармоник с шумом по амплитуде в 20 (А) и 40 (Б) процентов. | |
При добавлении того же уровня шума по фазе качество ухудшается сильнее. Уже при 20% шума качество восстановления среднее. Таким образом, фазы вносят больший вклад в общий вид восстановленной функции.
А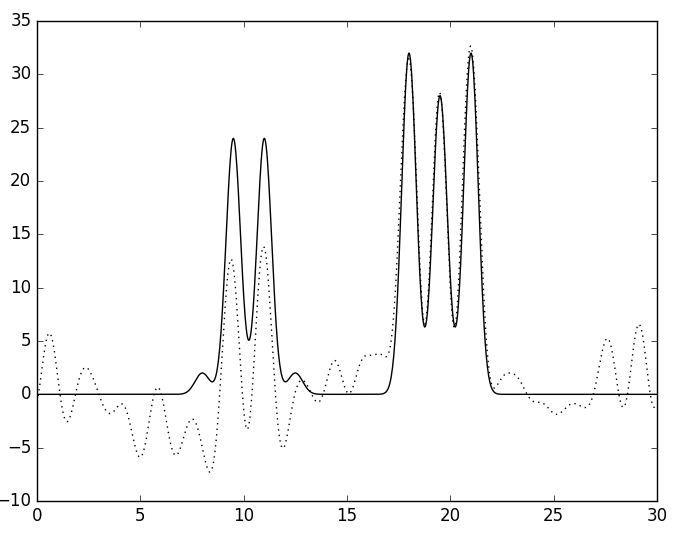
|
Б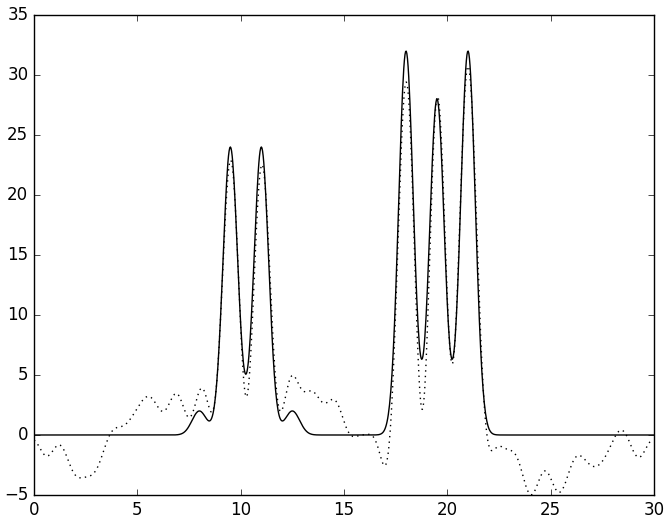
|
| Рис. 7. Восстановленная функция ЭП по полному набору гармоник с шумом по фазе в 20 (А) и 40 (Б) процентов. | |
Неполные наборы гармоник
Следующим этапом функция ЭП была восстановлена по неполному набору гармоник. Сначала удаляли первые 1, 2 или 3 гармоники (см. рис. 6). При удалении одной гармоники график смещается вниз, так как первая гармоника - константа. При удалении двух первых гармоник возникает волнообразный "прогиб". При удалении трёх - появляется периодичность в "прогибе". При этом положение атомов определить всё так же легко.
А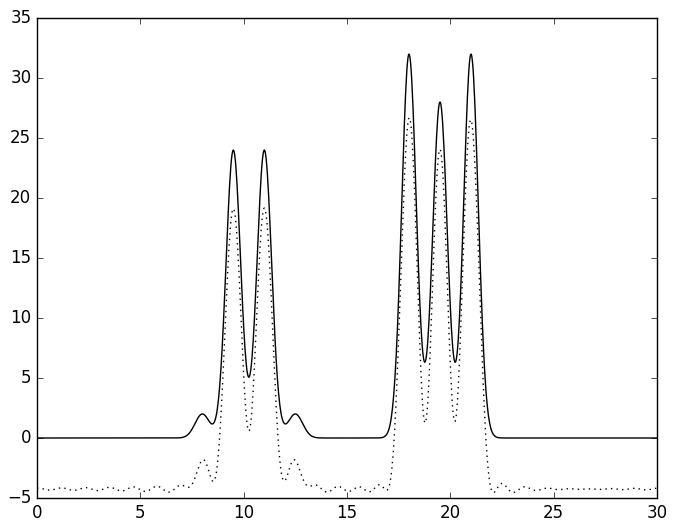
|
Б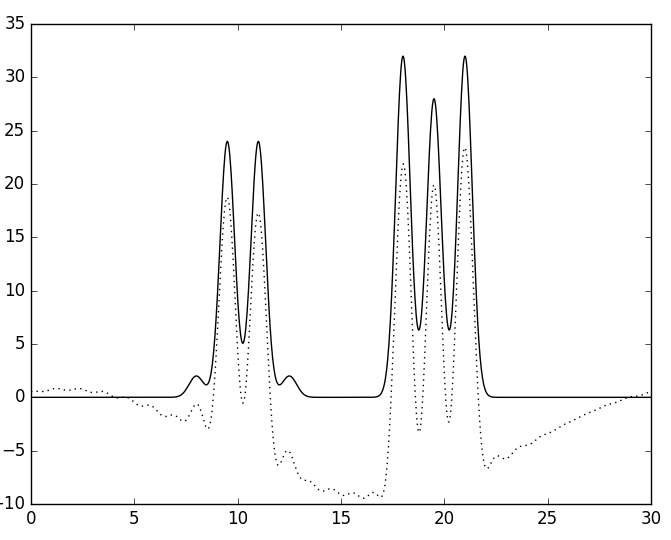
|
В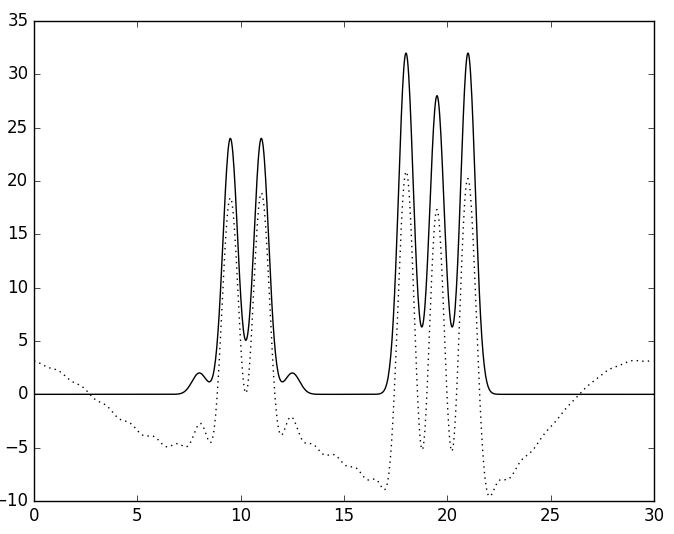
|
| Рис. 6. Восстановленная функция ЭП по неполному набору гармоник. А - без первой гармоники, Б - без первых двух, В - без первых трёх. | ||
Затем удаляли по две гармоники из середины - 9-10 и 13-14 (см. рис. 7). При удалении гармоник с бóльшими номерами качество восстановления остаётся лучше - хорошее.
А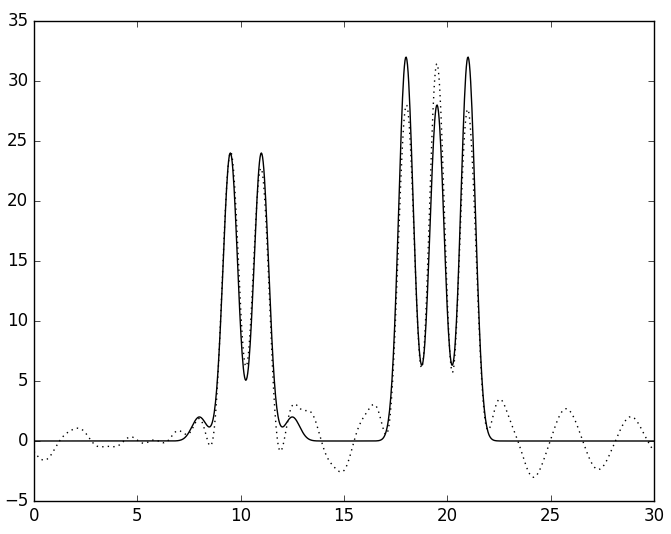
|
Б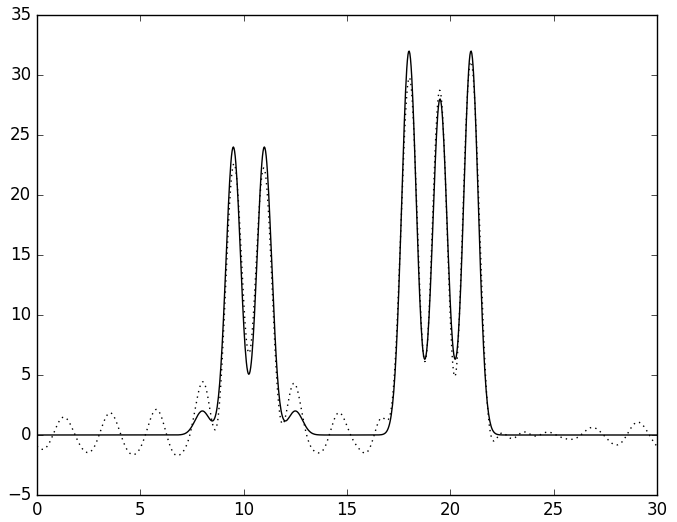
|
| Рис. 7. Восстановленная функция ЭП по неполному набору гармоник. А - без гармоник 9-10, Б - без гармоник 13-14. | |
Затем к этим неполным наборам добавили гармонику с номером n_0 + 10 = 36 и снова сделали восстановление (см. рис. 8). Добавление этой гармоники практически никак не изменило качество восстановления.
А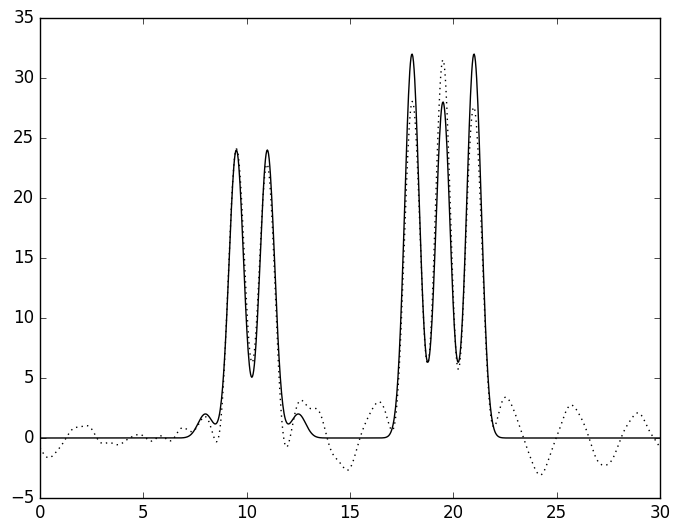
|
Б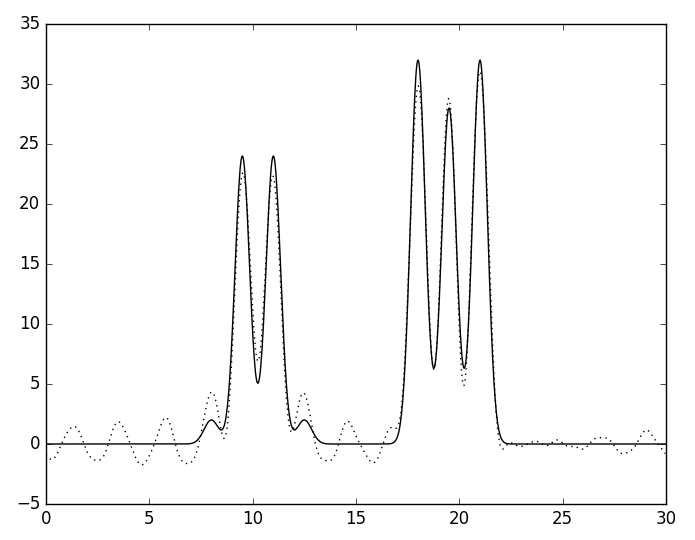
|
| Рис. 7. Восстановленная функция ЭП по неполному набору гармоник с добавлением гармоники №36. А - без гармоник 9-10, Б - без гармоник 13-14. | |
Напрашивающийся вывод - чем больше номер гармоники, тем меньший вклад она вносит в общий вид восстановленной функции ЭП. Это неудивительно, так как с увеличением номерам период уменьшается.
Определение разрешения
Для полного набора гармоник разрешение определяется как период гармоники с наибольшим номером и обозначается d. Для неполного набора строгого определения разрешения нет. Из предыдущих графиков мы увидели, что разрешение завсисит от количества недостающих гармоник. Следовательно, при вычислении разрешения было бы логично учитывать полноту данных - процент гармоник с длиной волны бóльшей d от размера полного набора.
Кроме того, важны и номера удалённых гармоник. Рисунок 7 показывает, что восстановление ЭП по наборам гармоник с одинаковыми полнотой и разрешением полного набора (92% и 1.15 Å) может быть разного качества. Наибольшие изменения в вид восстановленной функции вносят гармоники из середины набора.
Припишем каждой гармонике вес. Чтобы у серединных гармоник он был больше, чем у "краевых", была выбрана следующая функция:
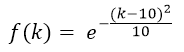
Она имеет максимум в точке 10 и, соответственно, будет давать наибольший вес гармоникам с номерами близкими к 10. Если просуммировать веса, то сумма будет тем больше, чем меньше гармоник из середины удалено. Так как мы хотим, чтобы разрешение увеличивалось при уменьшении этой суммы, то для подсчёта разрешения можем использовать следующую формулу:
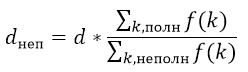
Итоговая таблица
В таблице приведены характеристики всех восстановлений функции ЭП. Разрешение для неполного набора гармоник посчитано по формуле, приведенной в предыдущем разделе.
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от F) |
Шум фазы (% от Р) | Качество восстановления |
| Полный набор гармоник | |||||
| 0-498 | 0.06 | 100 | 0 | 0 | отличное |
| 0-25 | 1.15 | 100 | 0 | 0 | отличное |
| 0-14 | 2 | 100 | 0 | 0 | среднее |
| 0-9 | 3 | 100 | 0 | 0 | плохое |
| 0-4 | 6 | 100 | 0 | 0 | плохое |
| 0-25 | 1.15 | 100 | 20 | 20 | среднее |
| 0-25 | 1.15 | 100 | 10 | 10 | среднее |
| 0-25 | 1.15 | 100 | 5 | 5 | хорошее |
| 0-25 | 1.15 | 100 | 20 | 0 | хорошее |
| 0-25 | 1.15 | 100 | 40 | 0 | среднее |
| 0-25 | 1.15 | 100 | 0 | 20 | среднее |
| 0-25 | 1.15 | 100 | 0 | 40 | среднее |
| Неполный набор гармоник | |||||
| 1-25 | 1.15 | 96 | 0 | 0 | отличное |
| 2-25 | 1.15 | 92 | 0 | 0 | отличное |
| 3-25 | 1.15 | 88 | 0 | 0 | отличное |
| 0-8; 11-25 | 1.84 | 92 | 0 | 0 | среднее |
| 0-12; 14-25 | 1.33 | 92 | 0 | 0 | хорошее |
| 0-8; 11-25; 35 | 1.84 | 92 | 0 | 0 | среднее |
| 0-12; 14-25; 35 | 1.33 | 92 | 0 | 0 | хорошее |