Построение функции электронной плотности

Модель для компьютерного эксперимента

Общее описание модели следующее. На отрезке [0,30] (ангстремы) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 5-7 атомов (2+3 или 2+3+2; возможны другие варианты). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.

В данной работе в качестве модели были выбраны две молекулы - аммиак и формальдегид, предполагаем наличие водородной связи H2C=O---H-NH2.

Функция задается на интервале [0,30] c помощью скрипта compile-func.py с параметрами, указанными ниже (команда). Моделируется 1D график электронной плотности молекулы. 30 следует понимать как 30 ангстрем.

Гауссова функция определяется числами lambda,beta,gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2, пример параметров скрипта:

• -g 30,3,3+40,3,4.3+2,3.5,6.5+30,3,7.5 (сумма четырех гауссовых функций: их max в точках 3,4.3,6.5,7.5, высота 30,40,2,30 соответственно; ширина "колокола" порядка 1; третий - низкий - пик моделирует атом водорода);
• Ширина колокола должна примерно соответствовать диаметру атома - порядка 1 с небольшим ангстрема (электронная плотность резко спадает на таком расстоянии от центра);
• Высота зависит от числа электронов в атоме.

В случае выбранной модели в данной работе использовались следующие параметры (подобраны для некоторого приближения к модели; скрипты compile-func.py, fourier.py,):

Функция имеет вид нескольких гауссовых кривых с центром в разных точках, она представлена на рисунке 1. Выходной файл скрипта compile-func.py - текстовый файл func.txt, в котором описана заданная функция (в виде пар X – Y).

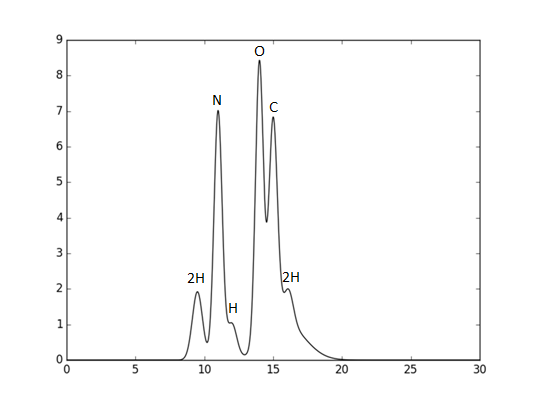
Рис.1. График заданной функции электронной плотности, заданная на отрезке [0,30] для выбранной модели из двух молекул.

Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py:

Полные наборы гармоник

Расчёт коэффициентов Фурье

Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта func2fourier.py:

Выходной файл скрипта func2fourier.py – текстовый файл func_ft.txt. В нём приведены амплитуды и фазы гармоник, а также их номера.

Отбор гармоник и восстановление функций

Из 499 гармоник были отбирались гармоники, с тем чтобы найти n0, для которого по графику восстановленной по полному набору гармоник (0, 1, ..., n0) функции можно было определить положение максимумов всех гауссовых слагаемых («отличное восстановление»):

На рисунках 2-7 представлены полученные функции (исходная - сплошная линия, функция по выбранным гармониками - пунктиром).

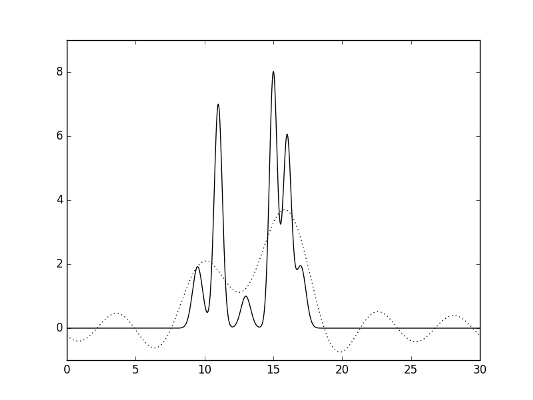
Рис.2. Гармоники 0-5.

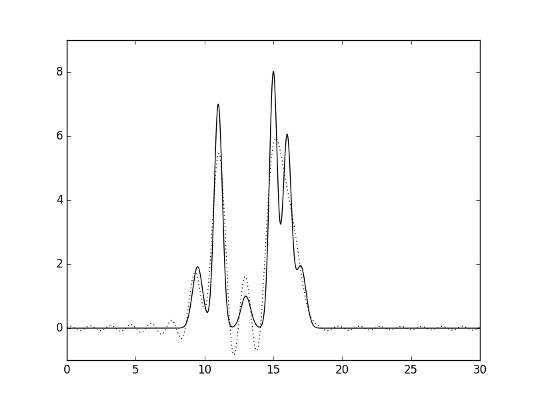
Рис.3. Гармоники 0-20.

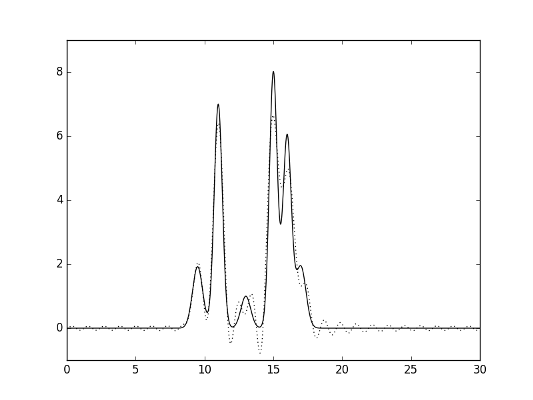
Рис.4. Гармоники 0-25.

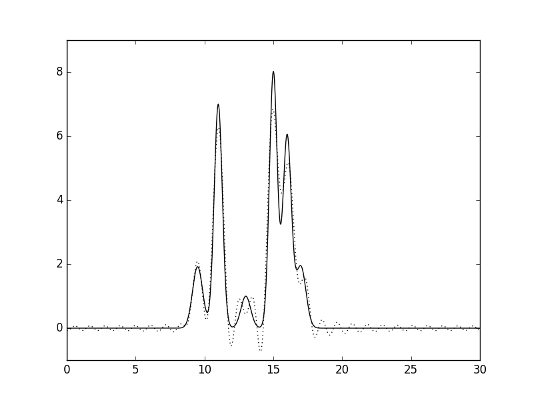
Рис.5. Гармоники 0-27.

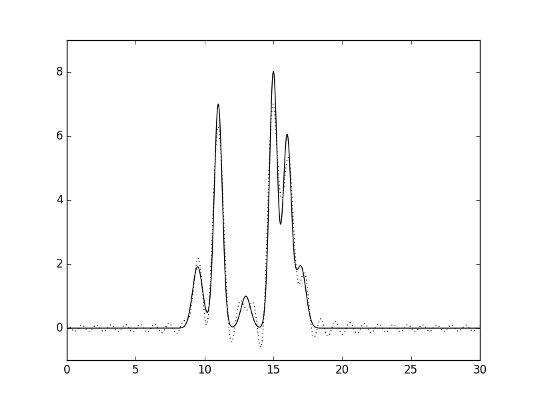
Рис.6. Гармоники 0-28.

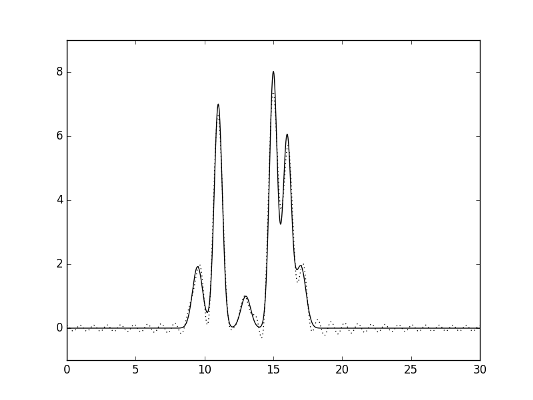
Рис.7. Гармоники 0-30.

Определено значение n0=30, при котором восстановление отличное, т.е. по графику восстановленной функции можно точно определить положение максимума всех гауссовых слагаемых функции ("атомов").

Также найдены соответствия между количеством слагаемых и хорошим (можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума), средним (положение каких-то атомов определить по восстановленной функции нельзя, других - можно) и плохим (положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы") восстановлениями. Данные соотвествия представлены в таблице 1.

Добавление шума

Затем к амплитудам и фазам был добавлен шум (20% к амплитуде; 20% к фазе; по 10% к амплитуде и фазе):

Восстановление функции производилось по полному набору гармоник 0, 1, ..., n0. Качество восстановления заметно снизилось (можно охарактеризовать его как «среднее»), что отражено на изображениях ниже (а также зафиксировано в таблице 1).

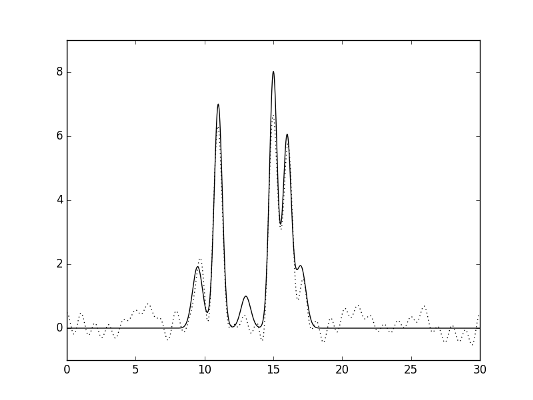
Рис.8. Гармоники 0-30, добавлен шум амплитуды.

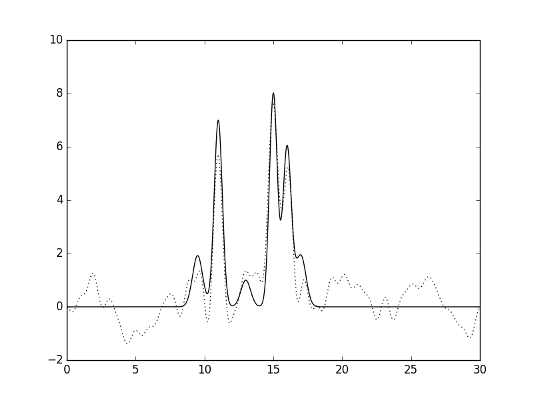
Рис.9. Гармоники 0-30, добавлен шум фазы.

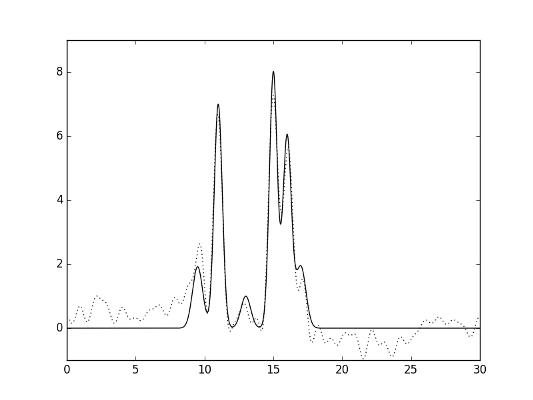
Рис.10. Гармоники 0-30, добавлен шум амплитуды и фазы.

Неполные наборы гармоник

Удаление гармоник из набора

Далее были удалены одна (номер 0) или две начальные гармоники (номера 0-1) из набора 0-34. Полученные графики приведены на рисунках 11 и 12, соответственно.

В случае удаления первой гармоники при последующем восстановлении функции видно, что она смещена по оси ординат; при этом результат восстановления можно считать «отличным». Это ожидаемый результат, так как значение первой гармоники равно числу F0 – первому коэффициенту ряда Фурье. В результате удаления первых двух гармоник восстановленная функция заметно искажается, однако значения максимумов еще можно определить.

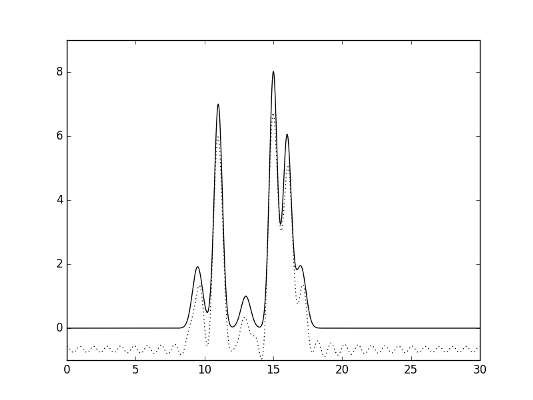
Рис.11. Гармоники 1-30.

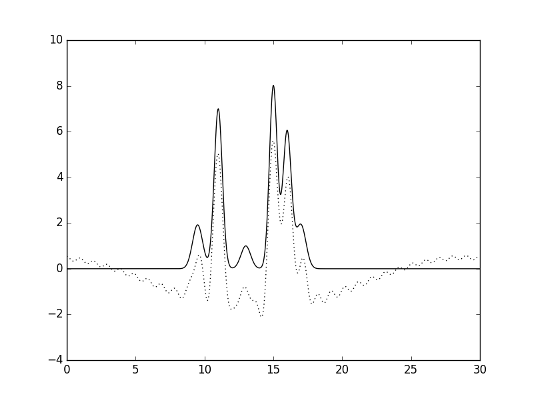
Рис.12. Гармоники 2-30.

Для получения неполного набора гармоник без 10% гармоник в его середине были удалены гармоники с номерами 12-15). Результат восстановления функции представлен на рисунке 13.

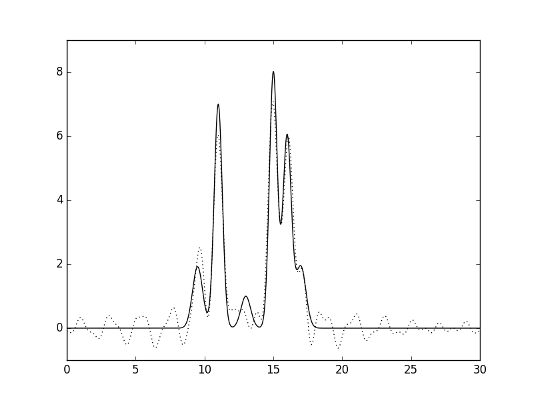
Рис.13. Гармоники 0-12,15-30.

Удаление как 14%, так и 8% гармоник в середине набора привело к ухудшению качества восстановления, его можно охарактеризовать как «среднее», хотя положение только атома 1 водорода из модели определить нельзя. Таким образом, вследствие удаления гармоник в середине набора максимумы от «атомов» становятся менее отличимы от шума

Добавление гармоники с большим номером

Добавление одной гармоники с номером, превышающим n0 на 10, т.е. 40-ой гармоники к набору 0-30 не привело к заметным изменениям (рисунок 24).

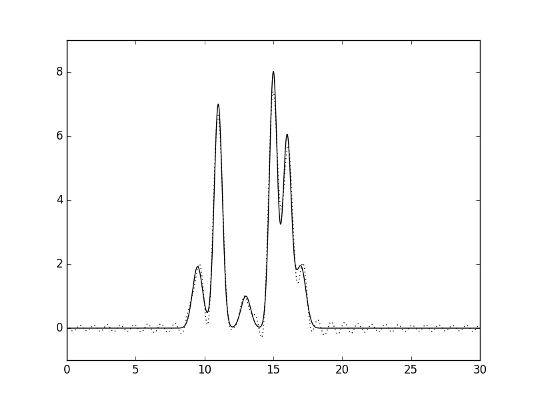
Рис.14. Гармоники 0-30,40.

Определение разрешения и полноты данных

В этом разделе представлена таблица с суммированной информацией о восстановлении функции по коэффициентам ряда Фурье. Также представлены данные о значениях разрешения восстановления. Некоторые пределения и пояснения к таблице см. на сайте kodomo.

Коротко, для полного набора гармоник разрешение определяется как период гармоники с наибольшим номером. Полнота данных вычисляется как процент гармоник в наборе, период которых не меньше разрешения, от числа гармоник в полном наборе для этого разрешения. Для полного набора полнота данных равна 100%.

Для неполного набора данных нет строгого определения разрешения, необходимо учитывать полноту данных. Для неполного набора полнота данных вычислялась как процент гармоник с длиной волны большей разрещения набора от числа гармоник в полном наборе. Для наборов гармоник 0,..., n, n+10 разрешением считалось таковое набора 0,..., n, а за полноту данных принималось 100%.

Таблица 1. Информация о восстановлении функции по коэффициентам ряда Фурье.

Набор гармоник	Разрешение	Полнота данных	Шум амплитуды	Шум фазы	Качество восстановления
	(A)	(%)	(% от величины F)	(% от величины phi)	(отличное, хорошее, среднее, плохое)
Полный набор гармоник
0-5	6	100%	0	0	Плохое
0-20	1,5	100%	0	0	Среднее
0-25	1,2	100%	0	0	Хорошее
0-27	1,1	100%	0	0	Хорошее
0-28	1,1	100%	0	0	Хорошее
0-30	1,0	100%	0	0	Отличное
0-30	1,0	100%	10	0	Среднее
0-30	1,0	100%	0	10	Хорошее
0-30	1,0	100%	10	10	Среднее
0-30	1,0	100%
Неполный набор гармоник
1–30	1,0	97%	0	0	Отличное
2–30	1,0	94%	0	0	Отличное
0–12, 15-30	1,0	90%	0	0	Среднее
0–30, 40	0,8	100%	0	0	Отличное

---