Описание используемой модели
На одномерном отрезке длиной 30Å и началом в 0 расположены две молекулы: 2 атома + 3 атома.
Атомы в каждой молекуле связаны ковалентно, и находятся на расстоянии 1-1.5Å
Молекулы расположены на расстоянии 4-5 Å (водородная связь или гидрофобное взаимодействие между ними).
Электронные плотности (ЭП) атомов описываются гауссовой кривой, формула которой представлена на Рисунке 1.
Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме.
Функция электронной плотности атомов на этом отрезке была задана с помощью скрипта compile-func.py.
График электронной плотности модели представлен на Рисунке 2. Параметры модели подобраны так, что возможно наблюдать за поведением как отдельных пиков, так и перекрывающихся (а так же пиков атомов участвующих в образовании водородной связи).
Скрипт задания модели
python ./compile-func.py -g 28,2,8+24,3,9.5+20,1,12.5+30,1.6,14+20,1,16.5
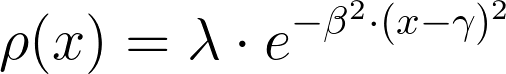
Рисунок 1. Формула гауссовой кривой, описывающей поведение электронной плотности в используемой модели. λ - высота гауссовской кривой, соответствующая максимуму электронной плотности в центре атома, β - ширина "колокола", примерно соответствующая диаметру атома, γ - координата максимума гауссовой кривой, соответстующая центру атома.
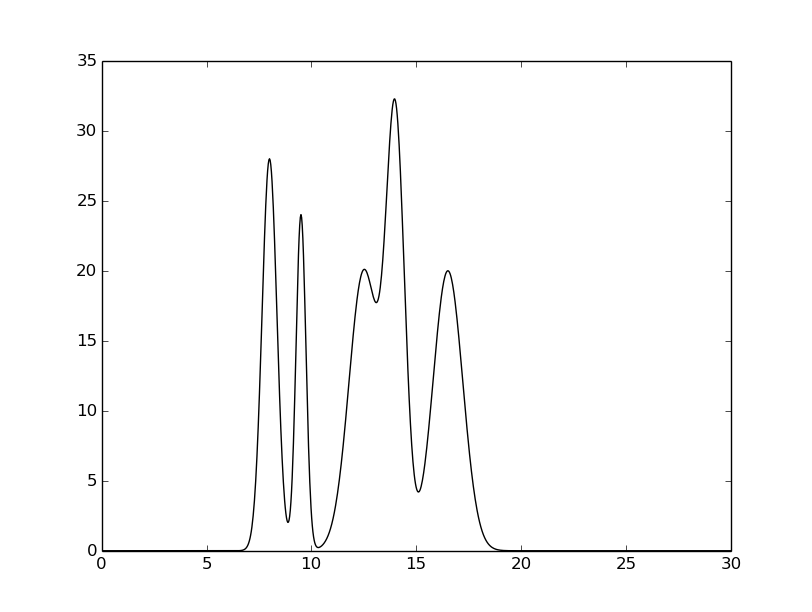
Рисунок 2. Электронная плотность исследуемой модели.  Данные в табулятивном формате.
Данные в табулятивном формате.
Расчёт коэффициентов Фурье
Полученаая функция электронной плотности разложена в ряд Фурье.
Коэффициенты разложения функции в ряд Фурье были получены с помощью скрипта  func2fourier.py
func2fourier.py
Скрипт раскладывает полученный ранее файл  func.txt(функцию ЭП) на 499 гармоник на отрезке [0 Å, 30 Å]. Выходной файл скрипта – файл
func.txt(функцию ЭП) на 499 гармоник на отрезке [0 Å, 30 Å]. Выходной файл скрипта – файл  func_ft.txt.
func_ft.txt.
Разложение в ряд Фурье функции ЭП
python func2fourier.py -i func.txt
Восстановление функции электронной плотности по амплитудам и фазам разложения Фурье
Введем критерии оценки качества восстановления:
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов");
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума;
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно;
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы".
Для полного набора гармоник
Для полного набора гармоник построен график восстановленной функции электронной
плотности модели с помощью скрипта  fourier2func.py.
Результат восстановления представлен на Рисунке 3.
fourier2func.py.
Результат восстановления представлен на Рисунке 3.
Восстановление функции ЭП по ее разложению в ряд Фурье
python fourier2func.py -f func.txt -i func_ft.txt -s
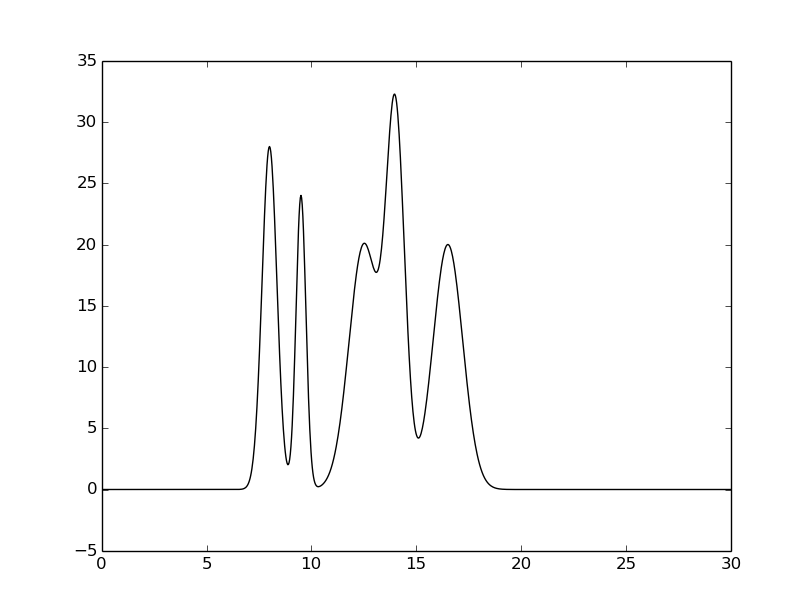
Рисунок 3. Восстановленная функция электронной плотности исследуемой модели.  Данные в табулятивном формате.
Данные в табулятивном формате.
Как видно из Рисунка 3, график восстановленной ЭП совпадает с графиком исходной ЭП (Рисунок 2), что говорит об отличном качестве восстановления. Поскольку полный набор включает 499 гармоник, то разрешение 0.06Å, что сильно избыточно. Попробуем найти минимально возможный набор гармоник, при котором наблюдается отличное качество восстановления.
Восстановление функции ЭП по ее разложению в ряд Фурье для некоторых гармоник
python fourier-filter.py -r 0-1 -i func_ft.txt -o ffr_1.txt
python fourier2func.py -f func.txt -i ffr_1.txt -o ffc_1.txt
python fourier-filter.py -r 0-10 -i func_ft.txt -o ffr_10.txt
python fourier2func.py -f func.txt -i ffr_10.txt -o ffc_10.txt
python fourier-filter.py -r 0-20 -i func_ft.txt -o ffr_20.txt
python fourier2func.py -f func.txt -i ffr_20.txt -o ffc_20.txt
python fourier-filter.py -r 0-30 -i func_ft.txt -o ffr_30.txt
python fourier2func.py -f func.txt -i ffr_30.txt -o ffc_30.txt
python fourier-filter.py -r 0-40 -i func_ft.txt -o ffr_40.txt
python fourier2func.py -f func.txt -i ffr_40.txt -o ffc_40.txt
python fourier-filter.py -r 0-25 -i func_ft.txt -o ffr_25.txt
python fourier2func.py -f func.txt -i ffr_25.txt -o ffc_25.txt
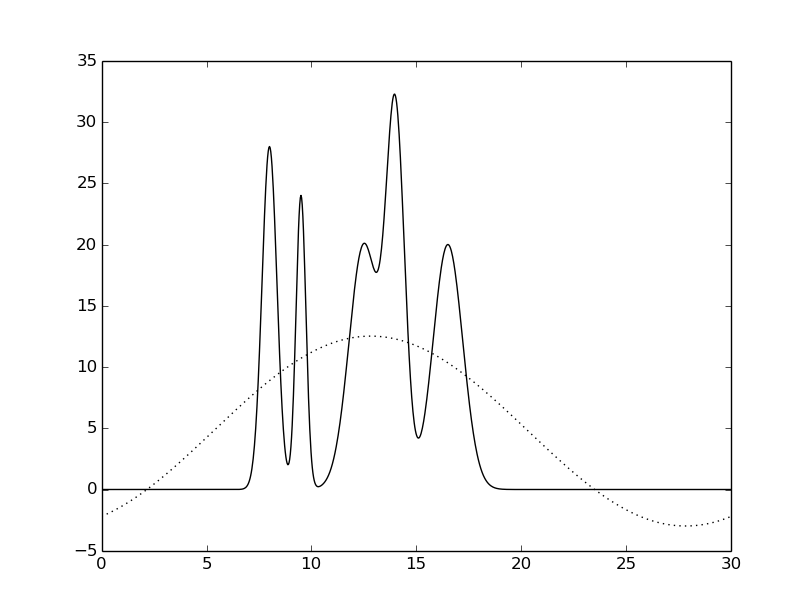 гармоники: 0-1 |
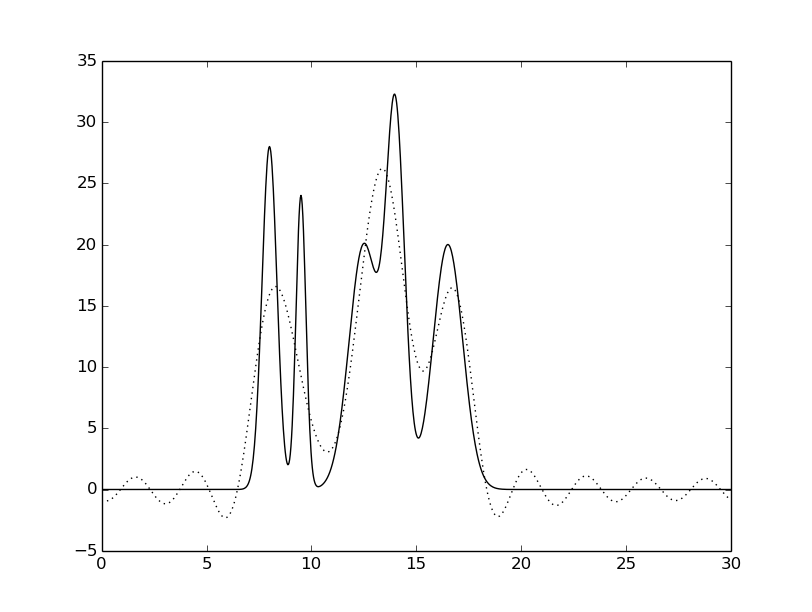 гармоники: 0-10 |
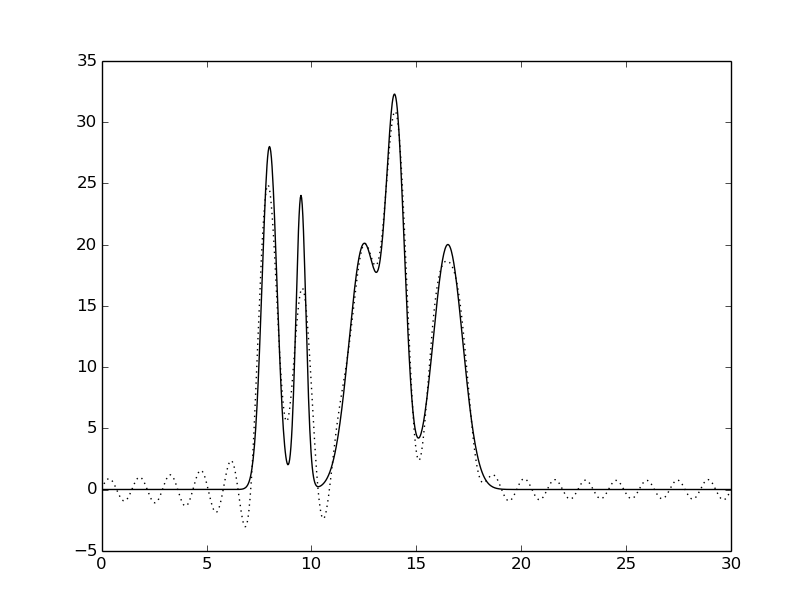 гармоники: 0-20 |
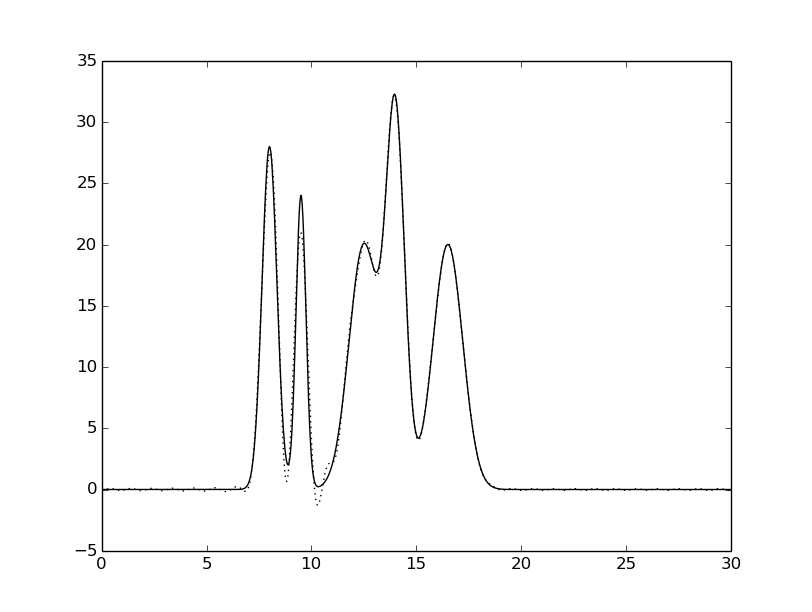 гармоники: 0-30 |
 гармоники: 0-40 |
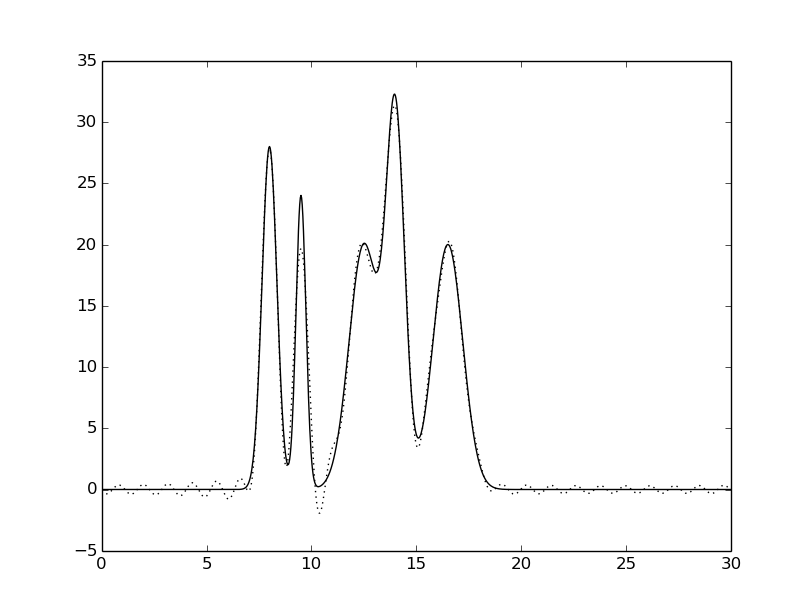 гармоники: 0-25 |
Рисунок 4. Восстановленная функция электронной
плотности исследуемой модели при различном числе гармоник.
Исходная функция – сплошной линией,
восстановленная функция – пунктирной линией.
Как видно из Рисунка 4, минимальный набор гармоник для отличного восстановления - 31.
Влияние шума на восстановление
Оценим влияние шума на восстановление: добавим шум к фазе, к амплитутде и к фазе и амплитуде разложения Фурье.
Добавление шума только к амплитуде
python func2fourier.py -F 7 -i func.txt -o ft_noise_F7.txt
python fourier-filter.py -r 0-30 -i ft_noise_F7.txt -o ft_noise_F7_30.txt
python fourier2func.py -i ft_noise_F7_30.txt -o func_noise_F7_30.txt
Добавление шума только к фазе
python func2fourier.py -P 7 -i func.txt -o ft_noise_P7.txt
python fourier-filter.py -r 0-30 -i ft_noise_P7.txt -o ft_noise_P7_30.txt
python fourier2func.py -i ft_noise_P7_30.txt -o func_noise_P7_30.txt
Добавление шума к фазе и амплитуде
python func2fourier.py -F 4 -P 4 -i func.txt -o ft_noise_F4P4.txt
python fourier-filter.py -r 0-30 -i ft_noise_F4P4.txt -o ft_noise_F4P4_30.txt
python fourier2func.py -i ft_noise_F4P4_30.txt -o func_noise_F4P4_30.txt
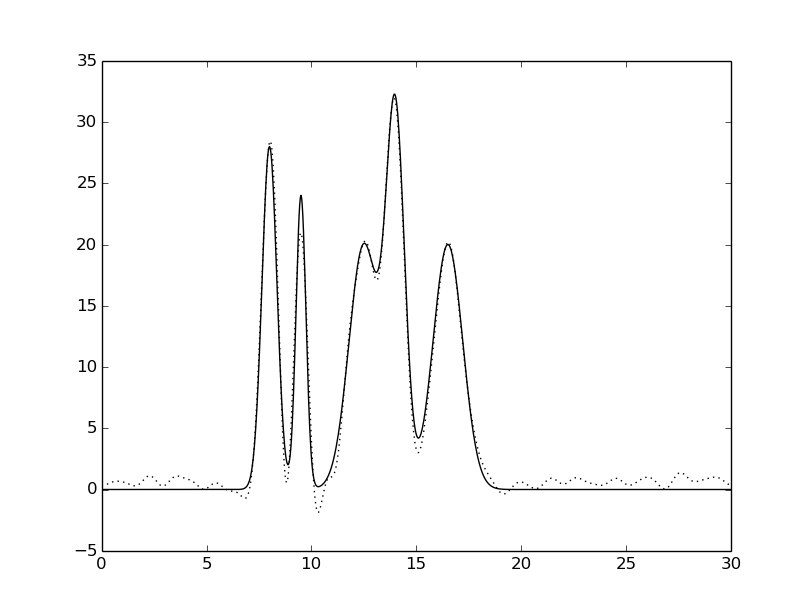 гармоники: 0-30 шум только к амплитуде |
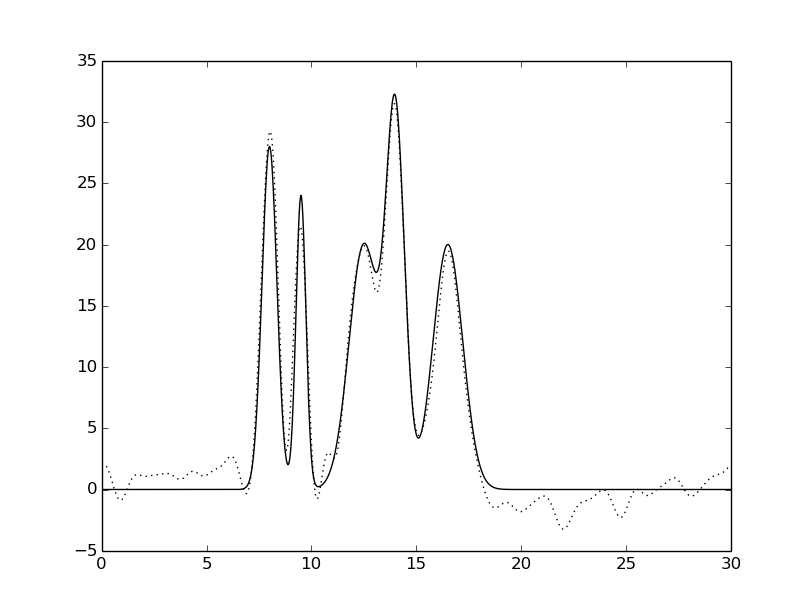 гармоники: 0-30 шум только к фазе |
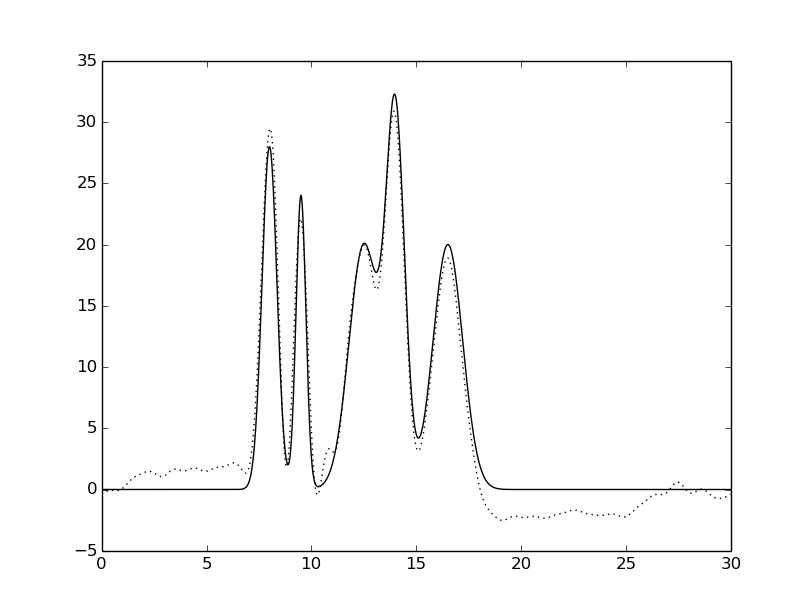 гармоники: 0-30 шум к фазе и амплитуде |
Рисунок 5. Восстановленная функция электронной плотности исследуемой модели при различных шумах при разложении. Исходная функция – сплошной линией,
восстановленная функция – пунктирной линией.
Из данных на Рисунке 5 видно, что шумы в фазе гораздо сильнее влияют на качество восстановления, чем шумы в амплитуде.
Для неполного набора гармоник
Оценим качество восстановления при различной полноте разложения.
Удаление первой гармоники
python fourier-filter.py -r 1-30 -i func_ft.txt -o ft_begin.txt
python fourier2func.py -i ft_begin.txt -o func_begin.txt
Удаление первых двух гармоник
python fourier-filter.py -r 2-30 -i func_ft.txt -o ft_begin2.txt
python fourier2func.py -i ft_begin2.txt -o func_begin2.txt
Удаление первых трех гармоник
python fourier-filter.py -r 3-30 -i func_ft.txt -o ft_begin3.txt
python fourier2func.py -i ft_begin3.txt -o func_begin3.txt
Удаление гармоник из середины набора (14-16)
python fourier-filter.py -r 0-13,17-30 -i func_ft.txt -o ft_mid.txt
python fourier2func.py -i ft_mid.txt -o func_mid.txt
Удаление гармоник из середины набора (12-18)
python fourier-filter.py -r 0-11,19-30 -i func_ft.txt -o ft_mid2.txt
python fourier2func.py -i ft_mid2.txt -o func_mid2.txt
Добавление гармоники с номером 30+10
python fourier-filter.py -r 0-30,40 -i func_ft.txt -o ft_append.txt
python fourier2func.py -i ft_append.txt -o func_append.txt
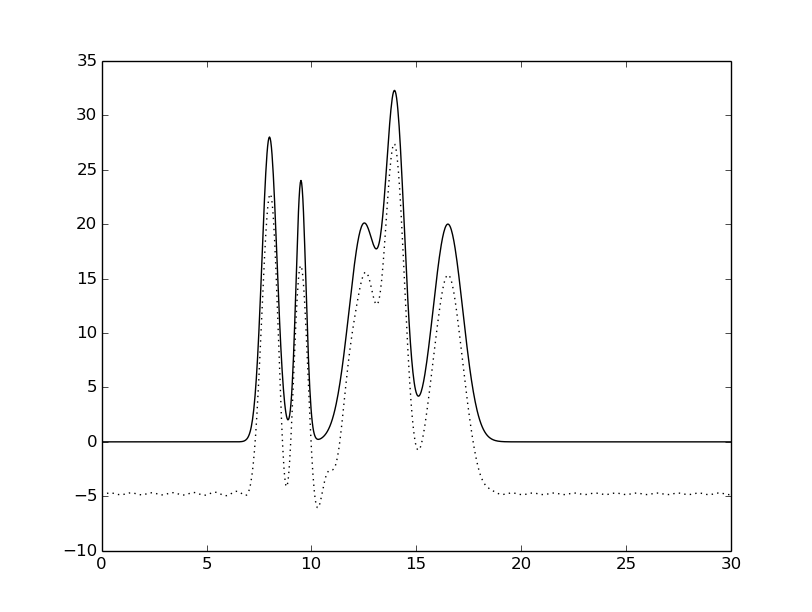 гармоники: 1-30 |
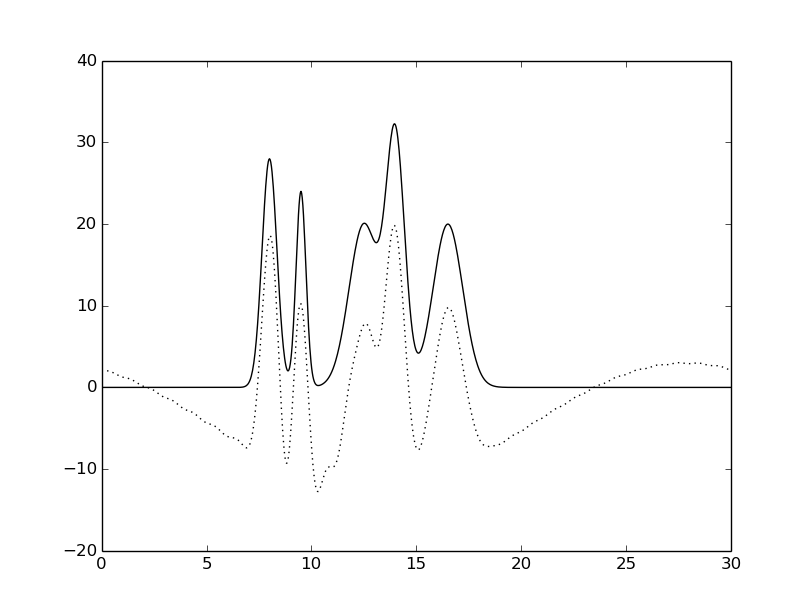 гармоники: 2-30 |
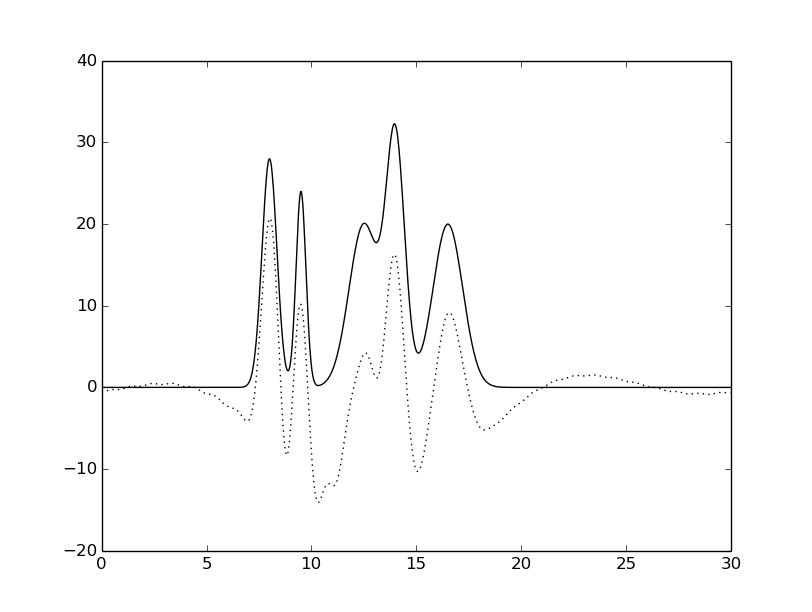 гармоники: 3-30 |
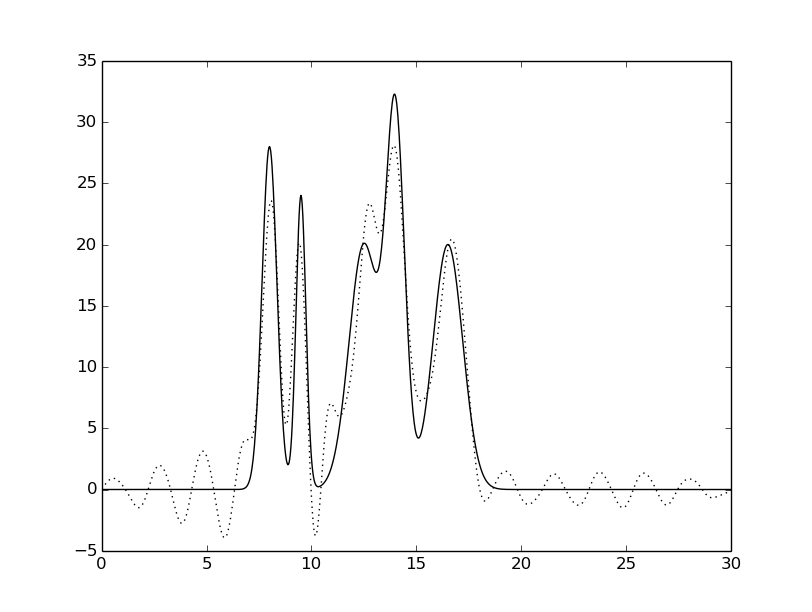 гармоники: 0-13,17-30 |
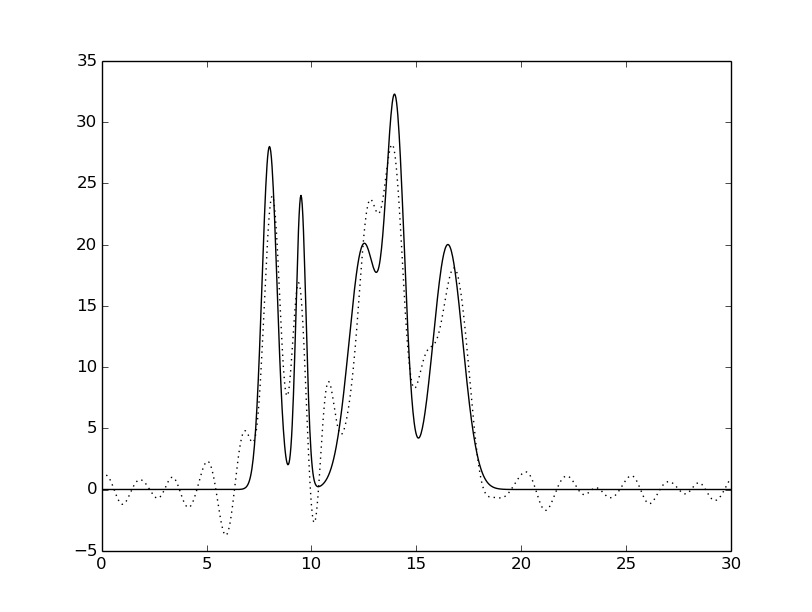 гармоники: 0-11,19-30 |
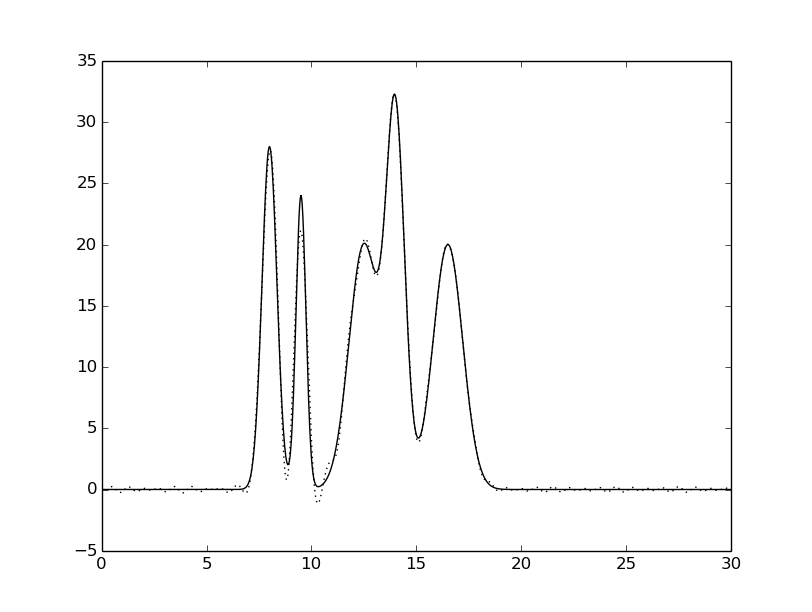 гармоники: 0-30,40 |
Рисунок 6. Восстановленная функция электронной
плотности исследуемой модели при различной полноте.
Исходная функция – сплошной линией,
восстановленная функция – пунктирной линией.
При удалении первой гармоники функция заметно смещается вниз по оси ординат,
это ожидаемо, т.к. значение первой гаромоники равняется первому коэффициенту ряда Фурье.
Если удалить первые две или три гармоники, то от функции вычитается синусоида с большим периодом.
Есил удалить около 10% гармоник из середины набора, то качество восстановления значимо ухудшается
Добавление гармоники с номером 40 к набору гармоник 0, 1, ..., 30, никак не повлияло.
Значит, что при восстановлении функции наиболее значимый вклад восят гармоники, которые находятся в середине набора.
Определение разрешения набора гармоник
Разрешение для полного набора гармоник для данной модели и ее разложения 0, 1, ..., 30 равно 30 Å / 31 ≈ 1,0 Å.
Полнота данных вычисляется как процент гармоник в наборе,
период которых не меньше разрешения,
от числа гармоник в полном наборе для этого разрешения.
Для полного набора полнота данных равна 100%.
Для неполного набора гармоник нужно всегда указывать, дополнительно полноту данных.
| Набор гармоник | Разрешение (Å) | Полнота данных (%) | Шум амплитуды (% от F) | Шум фазы (% от phi) | Качество восстановления | |
|---|---|---|---|---|---|---|
| Полный набор гармоник без шумов | ||||||
| 0-498 | 0.06 | 100 | 0 | 0 | отличное | |
| 0-1 | 15 | 100 | 0 | 0 | плохое | |
| 0-10 | 2.7 | 100 | 0 | 0 | плохое | |
| 0-20 | 1.4 | 100 | 0 | 0 | среднее | |
| 0-25 | 1.2 | 100 | 0 | 0 | хорошее | |
| 0-30 | 1.0 | 100 | 0 | 0 | отличное | |
| 0-40 | 0.73 | 100 | 0 | 0 | отличное | |
| Полный набор гармоник с шумами | ||||||
| 0-30 | 1.0 | 100 | 7 | 0 | хорошее | |
| 0-30 | 1.0 | 100 | 0 | 7 | среднее | |
| 0-30 | 1.0 | 100 | 4 | 4 | среднее | |
| Неполный набор гармоник | ||||||
| 1-30 | 1.0 | 96.8 | 0 | 0 | отличное | |
| 2-30 | 1.0 | 93.5 | 0 | 0 | отличное | |
| 3-30 | 1.0 | 90 | 0 | 0 | хорошее | |
| 0-13, 17-30 | 1.0 | 90 | 0 | 0 | среднее | |
| 0-11, 19-30 | 1.0 | 77 | 0 | 0 | среднее | |
| 0-30, 40 | 1.0 | 100 | 0 | 0 | отличное | |
