• Главная
• Семестры

  Семестр I

  Семестр II

  Семестр III

  Семестр IV

  Семестр VII

  Семестр VIII

• Проекты
• О себе
• Заметки
• Ссылки

Задание функции

Для компьютерного анализа была выбрана линейная атомная модель, изображённая на рисунке 1.

Рисунок 1. Модель атомов, расположенных в линию. Линии между атомами изображают взаимодействие между ними.

Числа 10,2,5 (например) описывают гауссову функцию в центре 5, высотой 10, шириной "колодца" ~1.

На основании данной модели была задана функция, описывающая линейную электронную плотность, с помощью скрипта compile-func.py командой:

Её график представлен на рисунке 2, а поточечные координаты - в файле func.txt .

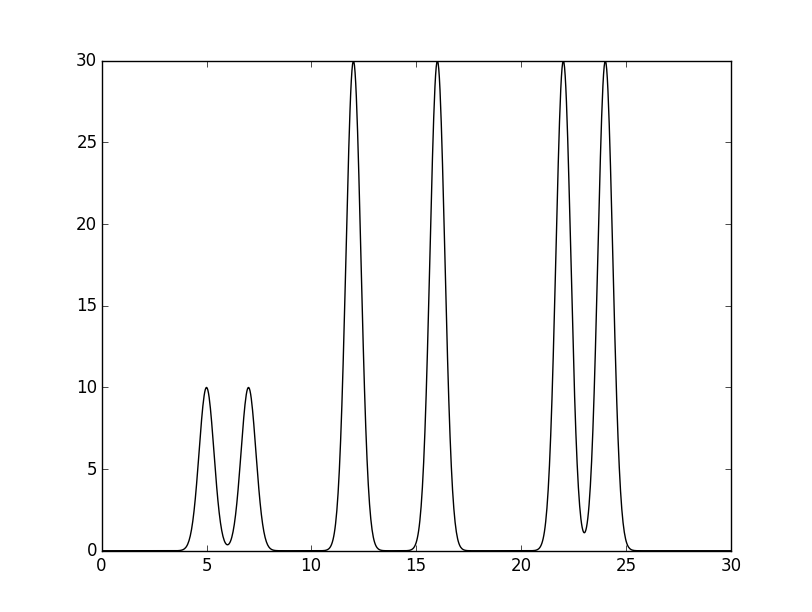
Рисунок 2. 1D график электронной плотности модели, изображённой на рис. 1. По оси х отложена длина в Å.

Разложение в ряд Фурье

Полученная функция была разложена по Фурье (на отрезке [0:30]) на 499 гармоник с помощью скрипта func2fourier.py командой:

Коэффициенты гармоник (амплитуды и фазы) представлены в файле .

Восстановление функции электронной плотности по амплитудам и фазам

По амплитудам и фазам полного набора гармоник

По полному набору гармоник была восстановлена первоначальная функция электоронной плотности с помощью скрипта fourier2func.py командой:

Разрешение вычисляется как отношение длины отрезка Т (30Å) к номеру последней гармоники.

График восстановленной функции представлен на рисунке 3. График восстановленой функции не отличим от графика первоначальной функции, восстановление отличное. При таком количестве гармоник (499) разрешение составляет 0.06 Å (см. табл. 1).

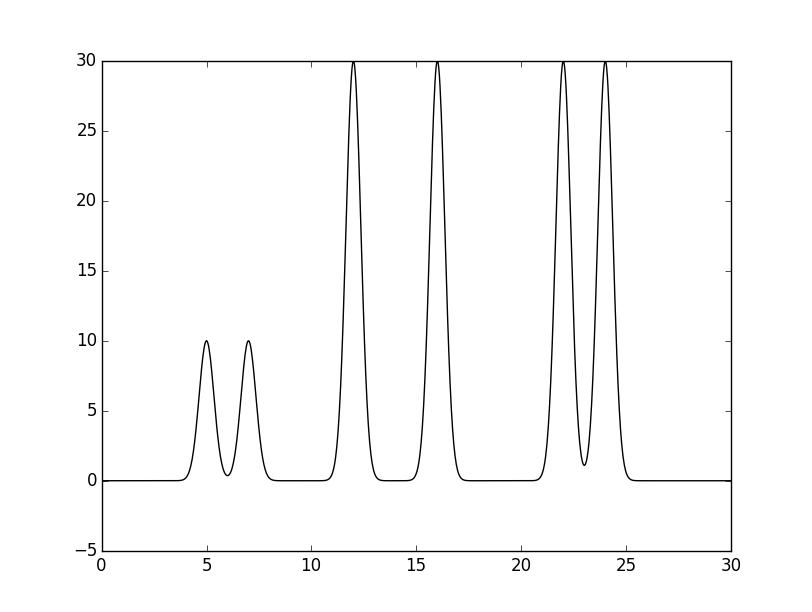
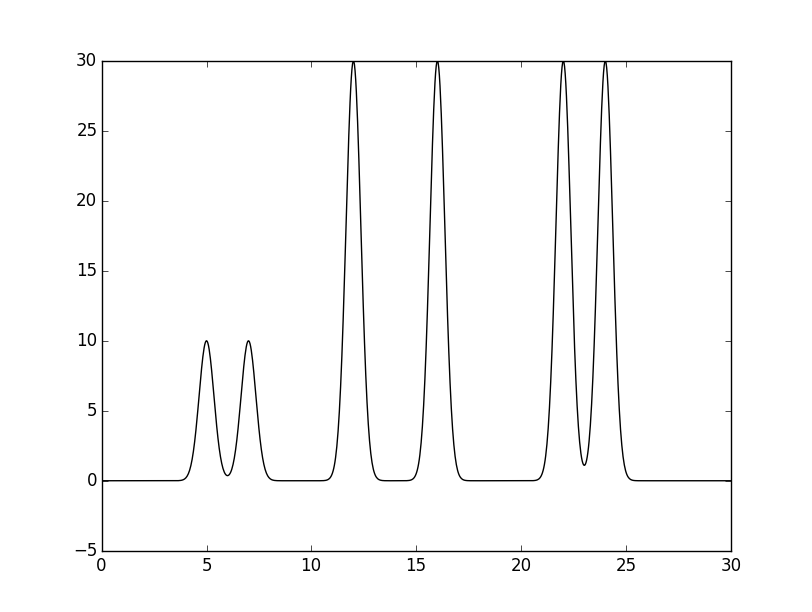
Рисунок 3. Графики изначальной функции электронной плотности (слева) и восстановленной по коэффициентам Фурье (справа).

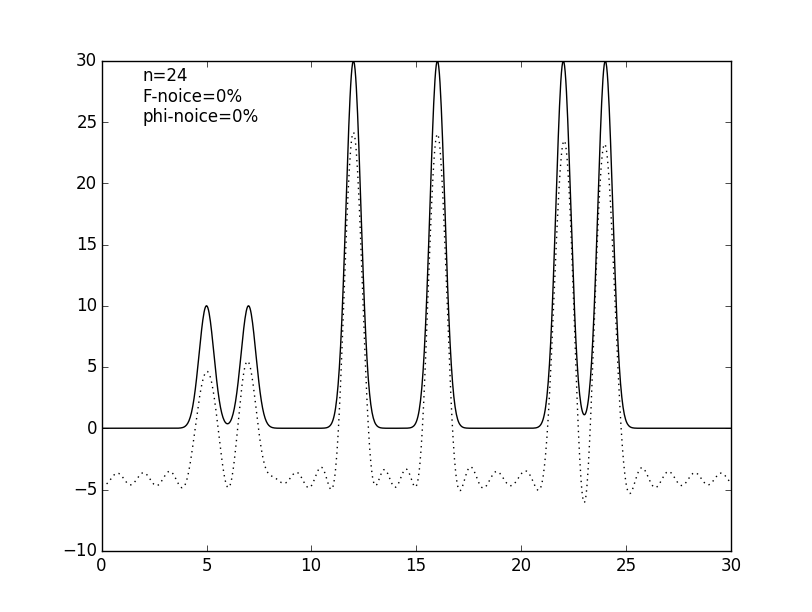
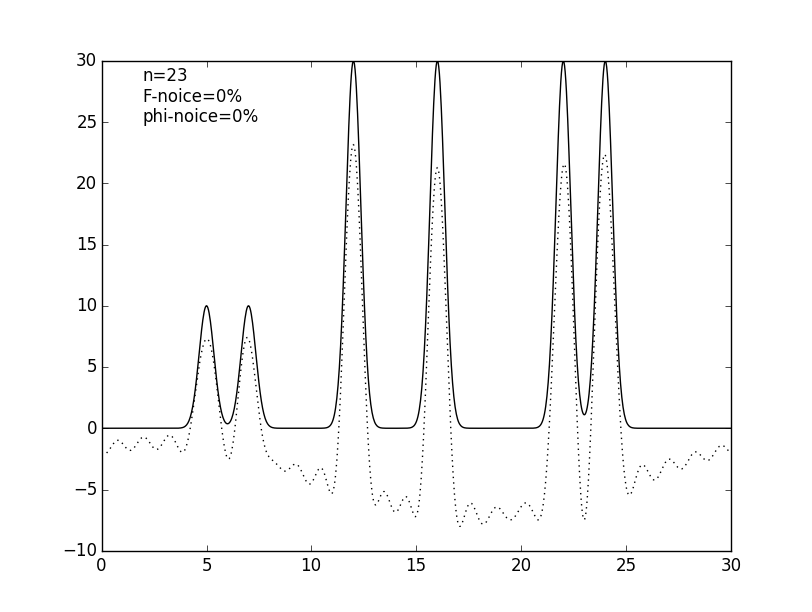
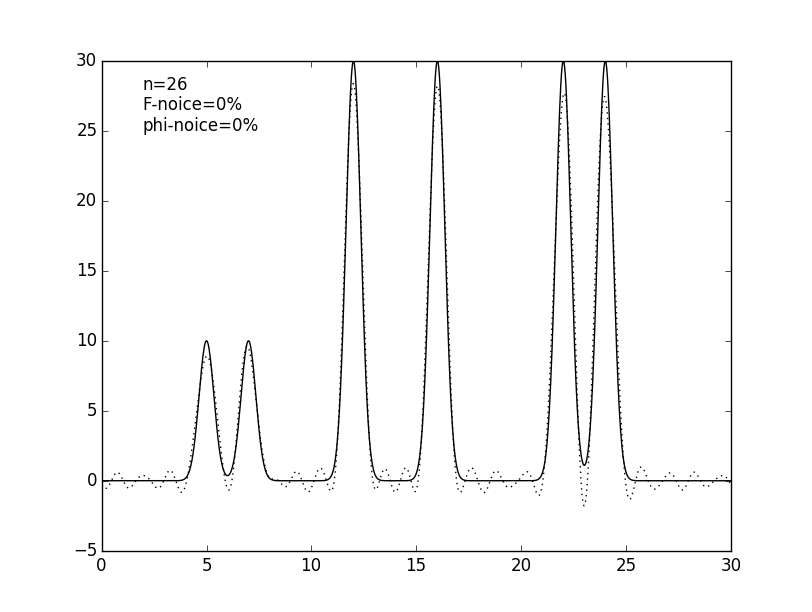
Чтобы приблизить условия компьютерного эксперимента к реальным, число гармоник было уменьшено до 25, дающих атомарное разрешение 1.2 Å. Также было проведено восстановелние функции электронной плотности по 9 (низкое разрешение), 12 (среднее), 17 (высокое) и 35 (субатомное) гармоникам (см. рис. 4 и табл. 1).

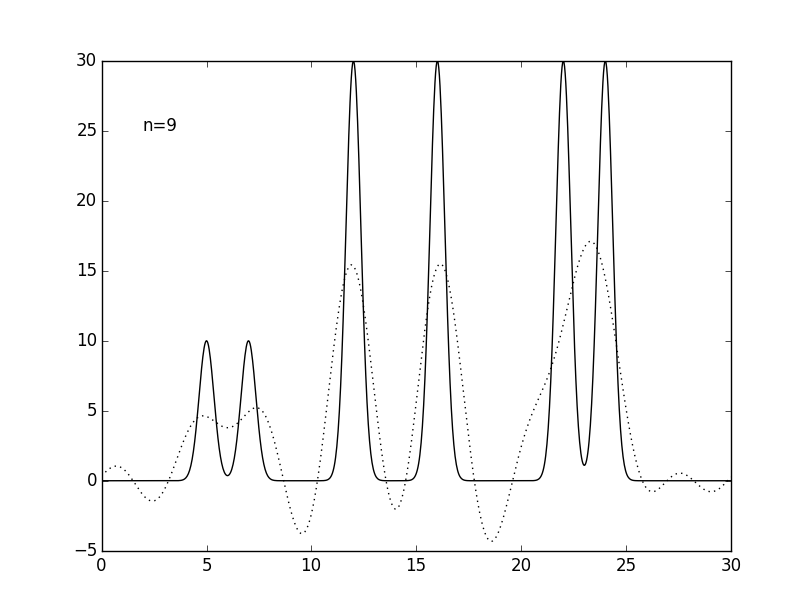
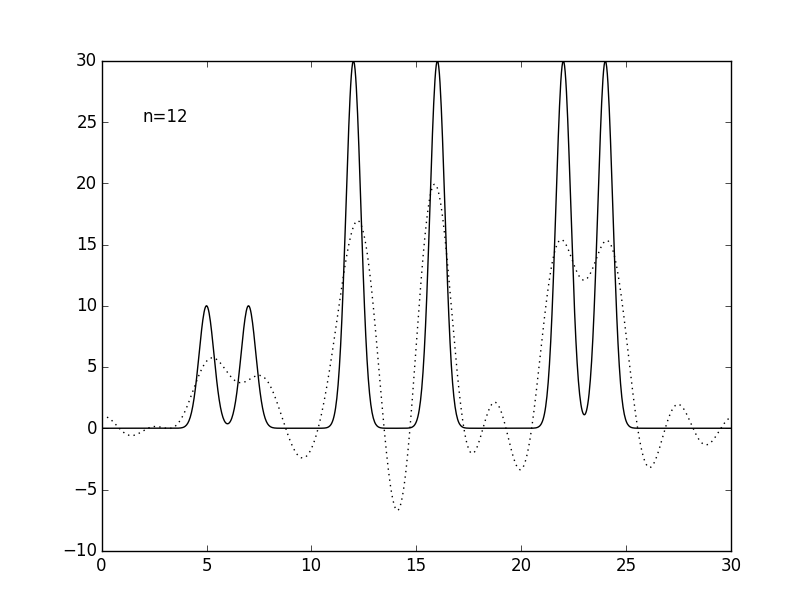
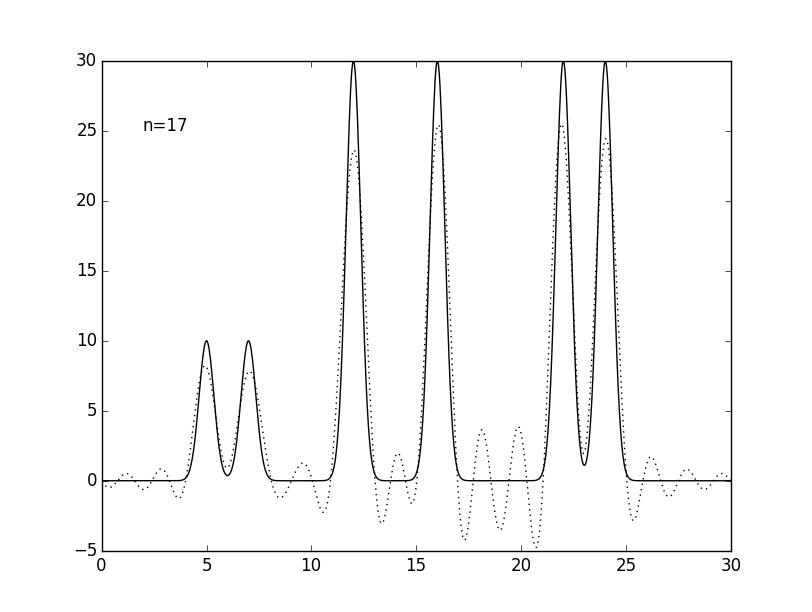
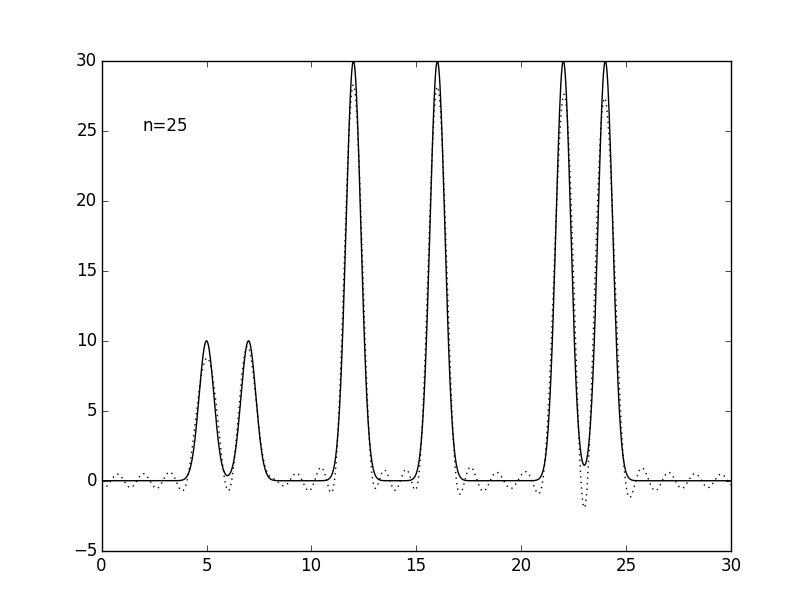
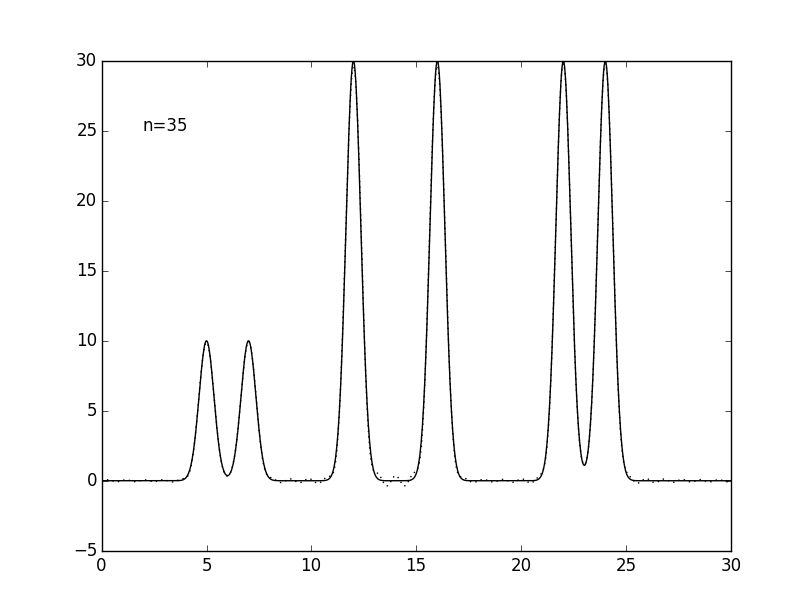
Рисунок 4. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 9, 12, 17, 25 и 35 гармоник (n).

Шум 20% означает, что к каждому значению Х прибавляется случайное число, распределенное нормально с параметрами: среднее = 0, среднее квадратичное отклонение (сигма)=0.2*Х

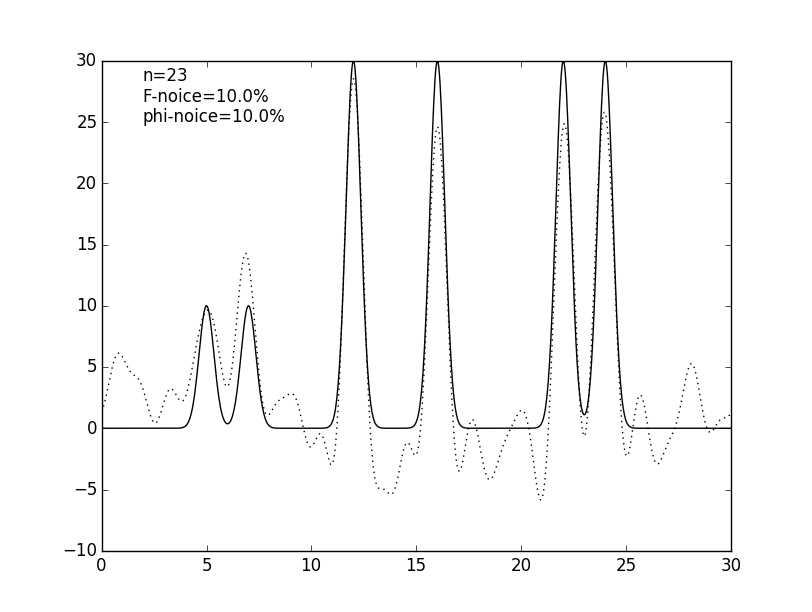
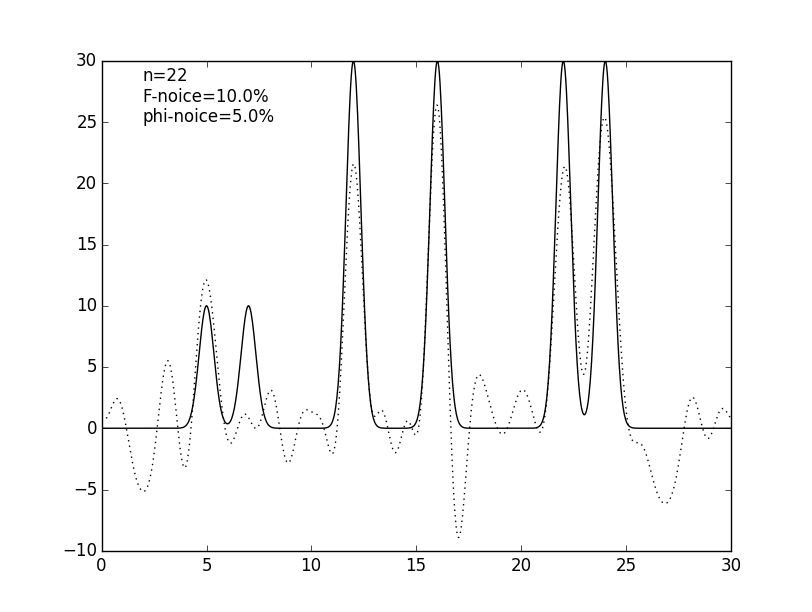
Чтобы ещё более приблизить эксперимент к реальным данным к значениям коэффициентов гармоник был добавлен шум: к значениям амплитуд (см. рис. 5 и табл. 1), к значениям фаз (см. рис. 6 и табл. 1) и сразу и к амплитудам, и к фазам (см. рис. 7 и табл. 1). Шум в амплитудах вносит небольшие изменения в востановленную функцию, в отличие от шума в фазах, который радикально меняет восстановление. Можно сделать вывод, что фазы вносят больший вклад в гармоники, чем их амплитуды.

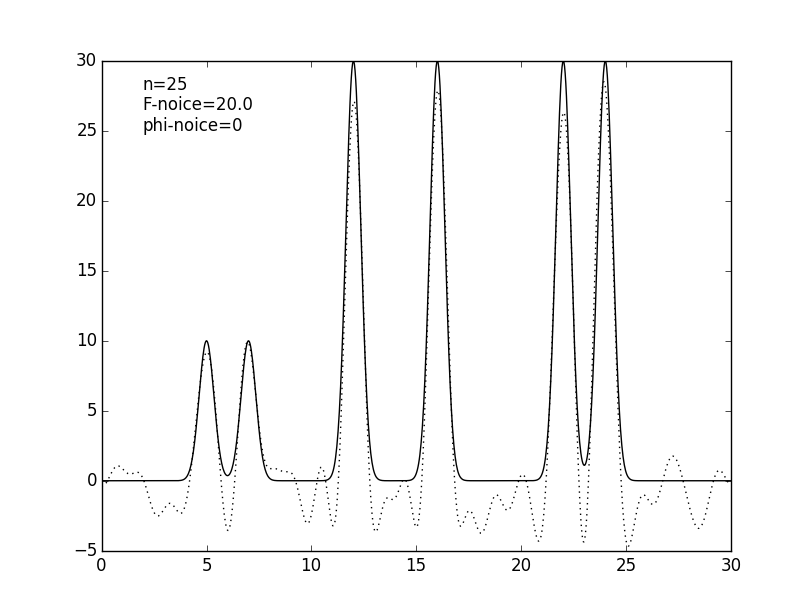
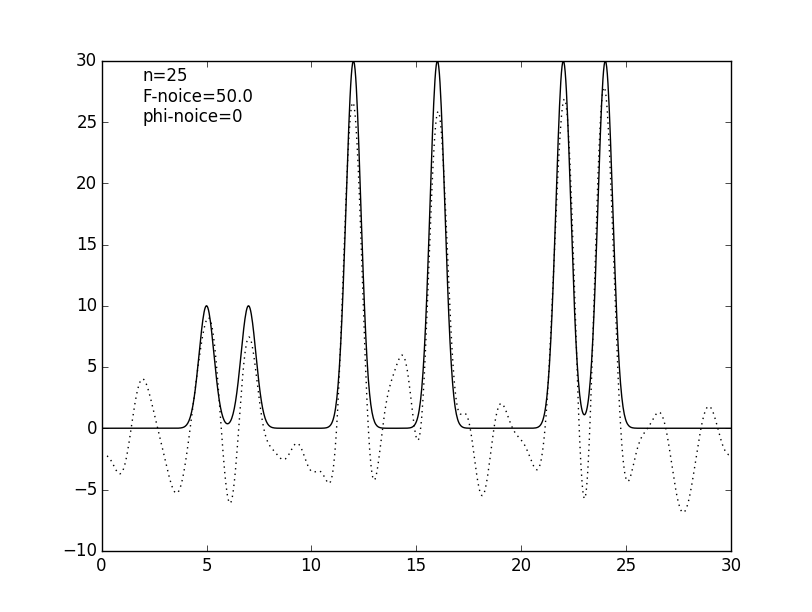
Рисунок 5. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 25 гармоник с шумом амплитуд 20% и 50%.

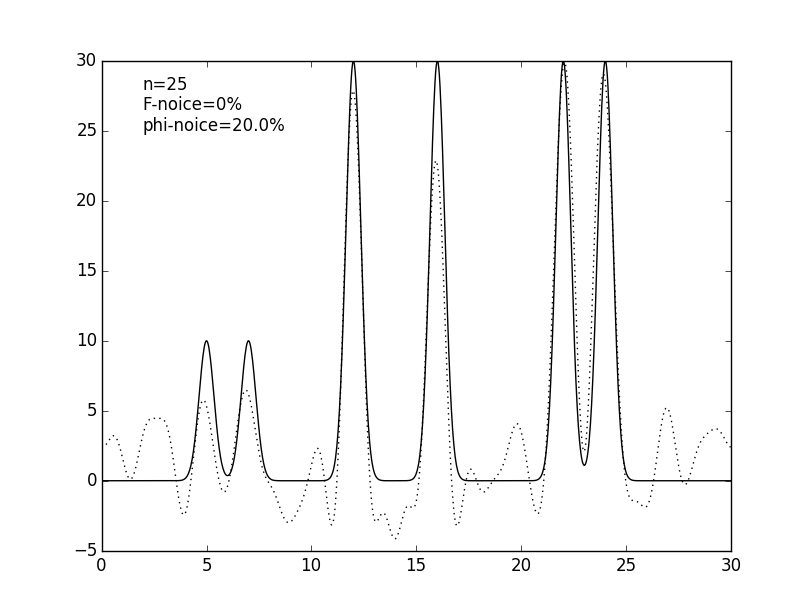
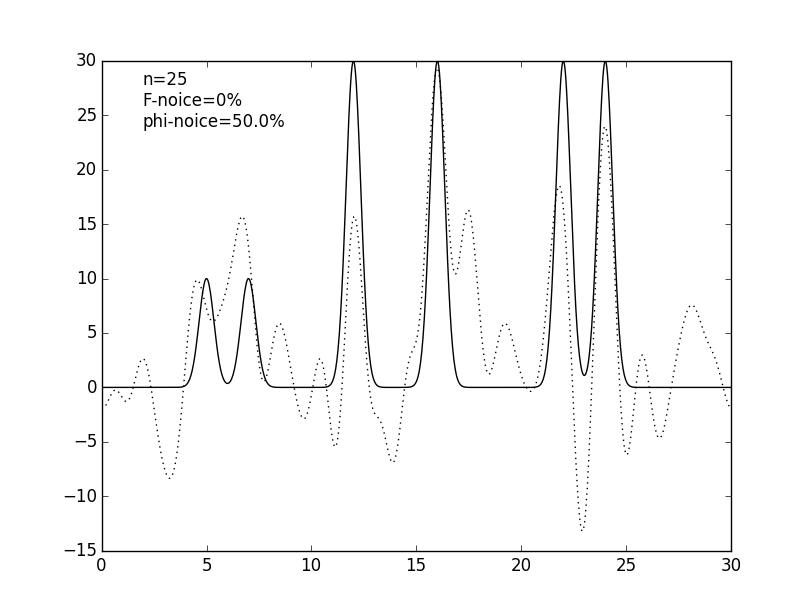
Рисунок 6. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 25 гармоник с шумом фаз 20% и 50%.

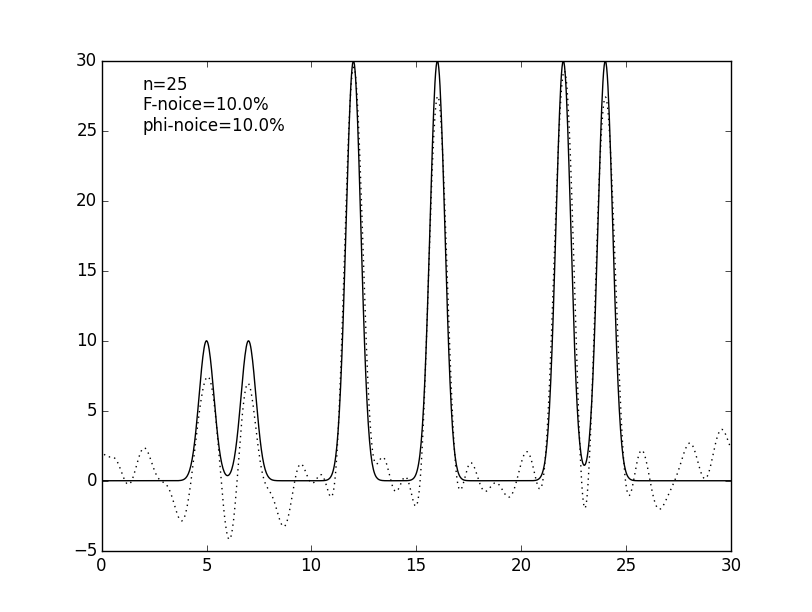
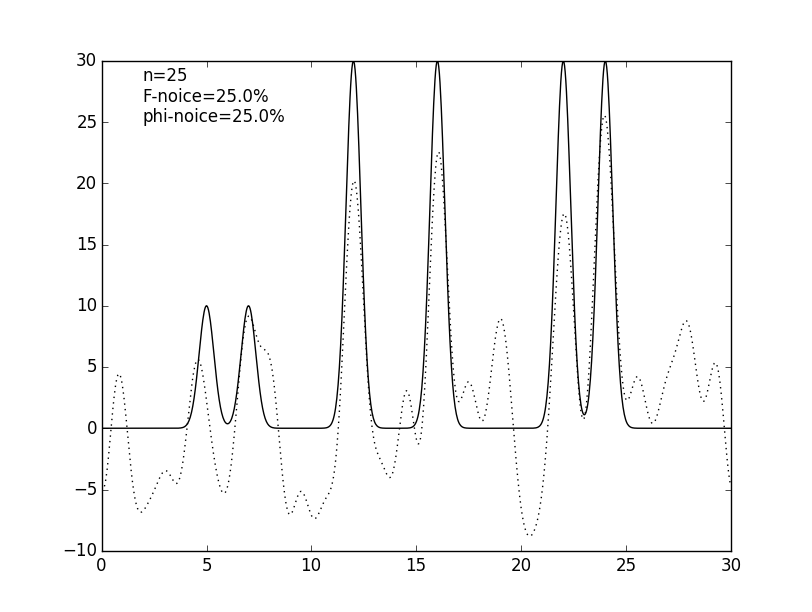
Рисунок 7. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 25 гармоник с шумом амплитуд и фаз по 10% и 25%.

По амплитудам и фазам неполного набора гармоник

В экспериментах часто определяются амплитуды не для всех гармоник, а для их части. Поэтому было смоделировано несколько ситуаций восстановления функции электронной плотности по неполному набору гармоник.

1. Если удалить первую или первые 2 гармоники, то вид восстановленной функции меняется характерным образом, причём качество восстановления не падает (особенно для человеческого глаза). Если удалить 1 гармонику, то вся функция просто перенесётся ниже, а если удалить 2 - то из функции вычтется синусоида с большим периодом (см. рис. 8 и табл. 1).

   
   Рисунок 8. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 1-24 гармоник (n=24) и для 2-24 гармоник (n=23).

2. Если удалить несколько гармоник из середины (8-12.5%), то восстановленная фукнция изменится куда сильнее (см. рис. 9 и табл. 1). Эти изменения похожи на внесение шума к амплитудам и фазам одновременно, но более регулярные. Напрашивается вывод, что гармоники из середины несут в себе больше всего информации.

   
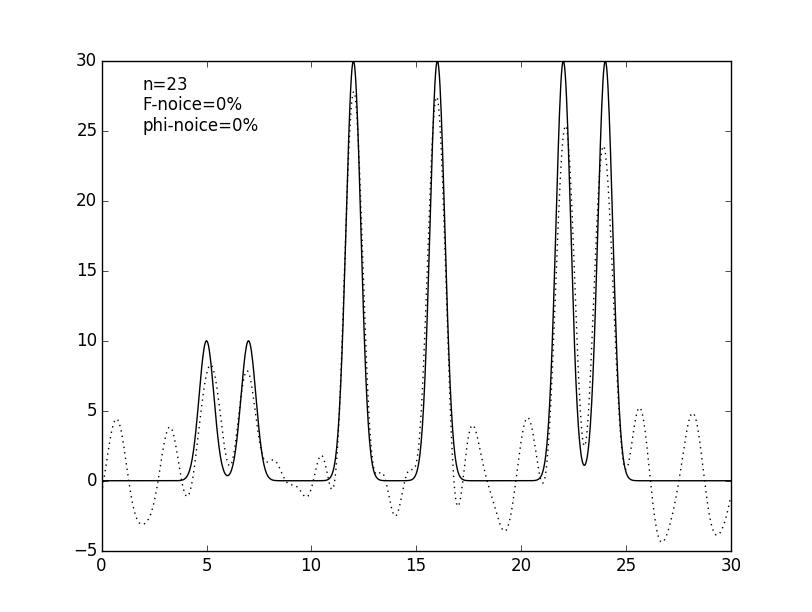
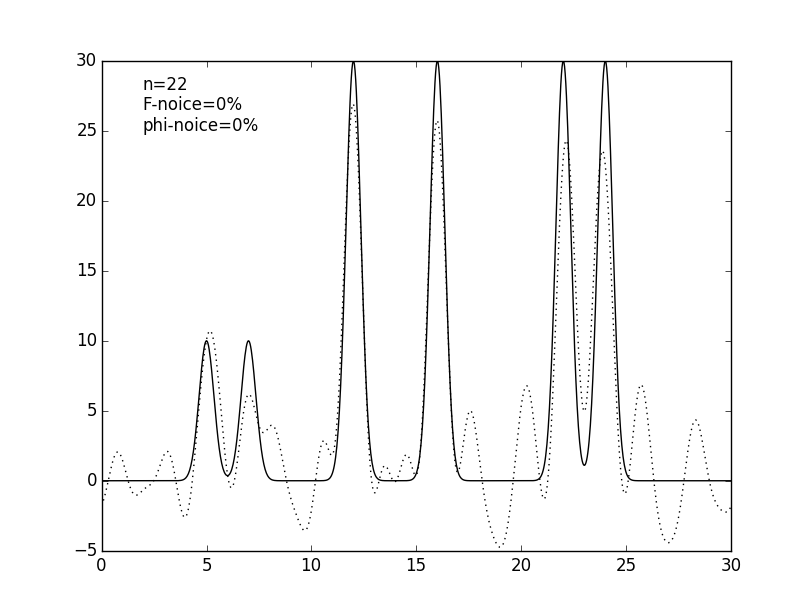
   Рисунок 9. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) без 2 (без 11,12-ой) и 3 (без 10-12-ых) гармоник из середины.

   На данном этапе можно сказать, что последние гармоники являются "уточняющими" (чем их больше, тем точнее приближение), первые - "базовыми" (задающие положение базовой линии), а гармоники из середины - смысловыми. Ещё хочется отметить, что бороться с недостающими гармониками должно быть проще, чем с шумом, в виду их регулярности.

3. Если к данному набору гармоник добавить ещё одну, номер которой превышает на 10 номер последней из имеющихся, то это ровным счётом ничего не изменит (см. рис. 10 и табл. 1).

   
   Рисунок 10. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 25 гармоник и для 25 гармоник с добавочной 35-ой.

4. Если смоделировать ситуации, максимально приближенные к реальной: 1) добавим по 10% шума к амплитудам и фазам, уберём вторую гармонику и гармонику из середины, 2) добавим 5% шума к фазам, 10% к амплитудам и уберём 6-ую, 12-ую и 18-ую гармоники, то "большие атомы" останутся по-прежнему различимы (в отличие от случая с низким разрешением), а вот "маленькие атомы" будут почти не отличимы от шума, т.е. как в большинстве случаев.

   
   Рисунок 11. Графики изначальной функции электронной плотности (сплошная линия) и восстановленной (пунктирная линия) для 25 гармоник и для 25 гармоник с добавочной 35-ой.

Определение разрешения набора гармоник

Для полного набора гармоник существует строгое определение разрешения - это длина волны гармоники с наибольшим номером.

Для неполного набора гармоник нет общепринятого строгого определения разрешения. Из полученных графиков понятно, что нехватка гармоник ухудшает разрешение, поэтому необходимо ввести коэффициент, учитывающий полноту гармоник, например: $$d=d_0/k$$ где d₀ - разрешение полного набора гармоник, k - полнота данных в долях единицы.

Вывод

Главными факторами, сильно влияющими на качество восстановления, являются высокий уровень шума фаз и большое количество недостающих гармоник из середины.

All Rights Reserved © 2012-2016 Popov