Филогенетические деревья.





- Джекнайф-анализ выравнивания мутированных последовательностей A,B,C,D,E и F. Сравнение методов bootstrap и jackknife.
- Редактирование дерева с помощью программы fretree. Отличия разных способов укоренения дерева.
- Изучение опций fdrawgram.
- Восстановление предковой последовательности методом максимального правдоподобия.
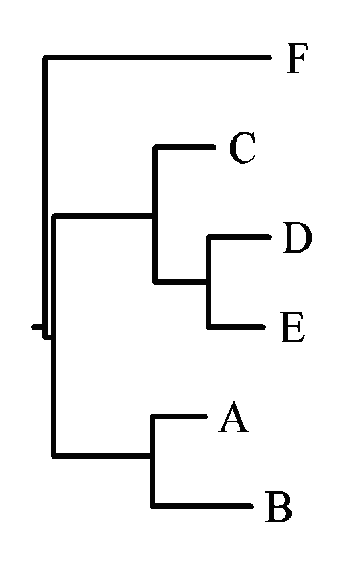
- Запустим программу fdnaml, значение параметра ttratio зададим равным 1. Получим дерево, топология которого совпадает с топологией нашего реального дерева (см. здесь)
- Воспользуемся программой fdnamlk, среди возможностей которой есть восстановление предковой последовательности по "современным". На вход этой программе подается файл с изучаемыми последовательностями, а также файл со скобочной формулой дерева с соответствующими листьями. Для того, чтобы программа в выходном файле выдала нам предковую последовательность, воспользуемся параметром -hypstate со значением y (да), кроме того, параметр ttratio выставим равным единице.
- К сожалению, fdnamlk выдает последовательности в очень неудобном формате: в виде выравнивания всех последовательностей - листьев, корня, узлов дерева. Это интересно в плане понимания, как программа реконструирует одну последовательность по нескольким, но неудобно для дальнейшей работы с восстановленными последовательностями. Чтобы извлечь необходимое нам (последовательности, лежащие в корне и узлах дерева) из выходного файла и поместить в отдельный файл, воспользуемся командой grep.
Выравнивание шести искусственно созданных на основе реально существующего гена последовательностей с названиями A,B,C,D,E и F было проанализировано с использованием метода jackknife. Коротко суть этого метода можно описать как создание из столбцов выравнивания длиной n нуклеотидов нескольких (по умолчанию 100) выравниваний длиной n/2. При этом каждый новый столбец, входящий в выравнивание, выбирается случайным образом из столбцов первоначального. Описанную операцию проделывает программа пакета Phylip fseqboot. Заметим, что эта программа может работать с выравниваниями разными методами, к примеру, осуществлять начальные стадии бутстреп-анализа (см. здесь пункт шестой); выбор метода зависит от значения параметра -test: b - bootstrap (по умолчанию), j - jackknife и др.
По каждому из построенных выравниваний длины n/2 с помощью метода максимального правдоподобия восстанавливалось филогенетическое дерево; использовалась программа fdnaml, значение параметра -ttratio 1. Скобочные формулы - результаты работы fdnaml, сохраненные в файле с расширением treefile, были поданы на вход программе fconsense. Эта программа сравнивает деревья и выдает в качестве результата по умолчанию "дерево из ветвей, поддержанных большинством" (majority-rule tree). Это не то же самое, что консенсусное дерево, хотя бы потому, что последнее обычно небинарное. Вот какое дерево мы получили как результат jackknife-анализа:
Jackknife-дерево
+------D
+-------100.0-|
| +------E
+------|
| | +------A
| | +100.0-|
| +100.0-| +------B
| |
| +-------------F
|
+---------------------------C
|
Сравним полученное деревья с реальным деревом (см.здесь, упражнение 1) и с "деревом из ветвей, поддержанных большинством" в результате бутстреп-анализа (см. ниже, а также здесь, пятое упражнение). Критерием сравнения будет, прежде всего, топология, кроме того, обратим внимание на бутстреп-значения ветвей.
Bootstrap-дерево
+------D
+--------99.0-|
| +------E
+------|
| | +-------------F
| +-96.0-|
| | +------B
| +-98.0-|
| +------A
|
+---------------------------C
Близость топологии оценивалась с помощью сравнения ветвей как разбиений множества листьев
ABCDEF Реальное дерево Jackknife дерево Bootstrap дерево
1 ..**** + + +
2 ..***. + + +
3 ...**. + + +
Из таблицы видно, что все четыре дерева имеют одинаковую топологию.
Судя по бутстреп-значениям, все ветви имеют высокую степень достоверности, в случае jackknife-анализа вообще ни одно дерево в ста случаях не отличалось по топологии от реального (бутстреп-значения всех ветвей равны 100).
Таким образом, с помощью и bootstrap, и jackknife мы получили один и тот же результат с высокой достоверностью, предположительно из-за того, что у нас не очень сложная модель, программа fdnaml восстанавливает все деревья с большой достоверностью и, видимо, иного варианта результирующего дерева построить нельзя - всеми деревьями поддерживаются одни и те же ветви.
В пакете Phylip есть программа для редактирования уже построенных деревьев, называется она retree (в Linux-варианте - fretree). Следует, прежде всего, отметить очень удобный интерфейс этой программы: она позволяет видеть изменения, вносимые в редактируемое дерево, в реальном времени; для этого не нужно открывать и закрывать какие-либо новые файлы, все отражается мгновенно на экране. С помощью этой программы пользователь обладает достаточно широкими возможностями для редактирования дерева: можно поворачивать ветви, выходящие из одного узла, и менять их местами; укоренять дерево двумя способами: в среднюю точку и используя "аутгруппу"; удалять клады и ветви и записывать результат работы на любом этапе в файл. Мы использовали fretree, чтобы укоренить в среднюю точку дерево, построенное с помощью Neighbor-joining по выравниванию мутантных последовательностей A-F. Скобочную формулу этого дерева подали на вход fretree с помощью такой команды:
fretree 7 neighbor_tree_form.txtЧисло, в данном случае 7, означает число листьев в подаваемом дереве. Изначально дерево выглядело так:
,---------------------1:B ! ! ,---------------------------------------------------2:F --7---------------------8 ! ! ,-------------3:C ! `---------------------9 ! ! ,-------------4:D ! `----------10 ! `------------5:E ! `-----------6:AC такой скобочной формулой: (B:0.50446,(F:1.19129,(C:0.29960,(D:0.30967,E:0.28082):0.27249):0.51562):0.50135,A:0.26971); По ней можно подумать, что дерево небинарное (во внешней скобке указаны три ветви), однако на самом деле это способ сообщить нам, что дерево неукорененное. |
Кроме визуализации скобочной формулы, программа fretree предлагает набор однобуквенных команд, набрав одну из которых с клавиатуры, можно тем или иным образом изменить дерево или записать его скобочную формулу в файл. Каждый узел и лист дерева на схеме обозначен числом, что также необходимо для редактирования (для указания программе, с каким элементом дерева работать). Мы хотим укоренить дерево в среднюю точку; для этого следует выбрать букву-команду "M" (medium), больше никаких данных указывать не нужно: программа самостоятельно найдет среднюю точку и укоренит дерево в нее. В итоге получаем укорененное дерево:
,-------------------------------------------------------------------------2:F
!
! ,-------------------3:C
-11 ,--------------------------------9
! ! ! ,-------------------4:D
! ! `----------------10
`--8 `-----------------5:E
!
! ,-----------------6:A
`-------------------------------7
`--------------------------------1:B
Скобочная формула здесь такая:(F:1.14453,((C:0.29960,(D:0.30967,E:0.28082):0.27249):0.51562,(A:0.26971, B:0.50446):0.50135):0.04675); По формуле видно, что дерево укорененное. Некоторые расстояния изменились по сравнению с прошлой формулой, но те ветви, которые укоренение непосредственно не затронуло, остались той же длины (ветвь A, ветвь B). |
Как видим, при укоренении появляется дополнительный узел - корень (на схеме под цифрой 11).
В конце работы мы записываем скобочную формулу укорененного дерева в файл с помощью буквенной команды "W" (write). При этом нам задается вопрос, в виде укорененного (R, rooted) или неукорененного (U, unrooted) сохранять дерево (выбираем первый вариант). Скобочная формула при этом записывается в заранее выбранный файл (rooted.treefile).
Дополнительно укореним наше изначальное дерево (к которому можно вернуться, выбрав "U" - "undo") еще одним доступным способом, с использованием "аутгруппы" (outgroup). Для этого выберем команду O (outgroup) и "скажем" программе, какой узел будет новой аутгруппой (выбрав одно из имеющихся на изображении дерева чисел). В нашем случае как корень аутгруппы мы укажем тот узел, в который fretree укореняла дерево в прошлый раз - узел 8. Вот что получаем в итоге:
,------------------------------------------------------------2:F
,------------8
! ! ,---------------3:C
! `-------------------------9
! ! ,---------------4:D
-11 `------------10
! `--------------5:E
!
! ,-------------6:A
`------------7
`-------------------------1:B
Cкобочная формула такая: ((F:1.19129,(C:0.29960,(D:0.30967,E:0.28082):0.27249):0.51562):0.25067, (A:0.26971,B:0.50446):0.25067); |
,-------------------------2:F
!
! ,------------3:C
-11 ,----------------------9
! ! ! ,-------------4:D
! ! `---------10
`-------------------------8 `------------5:E
!
! ,-----------6:A
`---------------------7
`---------------------1:B
Следует сделать еще одно замечание о работе fretree: редактирование дерева с помощью fretree может изменяет топологию
дерева.
Такие команды, как "D" (delete) и "R" (rearrange) могут помочь удалить или восстановить ветви редактируемого дерева. Тем не менее,
есть команды, которые не
меняют топологию дерева - те же команды укоренения ("M" и "O"), или команды,
меняющие ветви определенного узла местами (по-разному это делают "T" - transpose и "F" - flip).
Узнать о смысле той или иной буквенной команды можно, набрав ? - появится краткий help к программе fretree.
Скобочную формулу можно визуализировать несколькими различными способами - в виде кладограммы, фенограммы и др. Определяя эти термины, мы сталкиваемся с противоречиями в терминологии. Согласно одной трактовке (материалы Википедии), названные понятия отличаются степенью представления информации о длинах ветвей. Кладограмма - филогенетическое дерево, не содержащее информации о длинах ветвей. Фенограмма (или филограмма) - филогенетическое дерево, содержащее информацию о длинах ветвей; эти длины представляют изменение некой характеристики. Однако в help к одной из программ-визуализаторов пакета Phylip (fdrawgram) кладограмма и фенограмма определяются иначе - это разные способы визуального представления деревьев. Кладограмма - это "v-образное" дерево; фенограмма - дерево с "квадратными" ветвями - нарисованное с использованием прямых линий и прямых и развернутых углов. Кроме этих типов, существуют другие, на наш взгляд, менее употребимые, к примеру, "курвиграмма" - ветви дерева в виде 1/4 эллипсов.
Нам необходимо визуализировать укорененное в прошлом упражнении дерево в виде фенограммы, листья которой обращены вправо. Так
как дерево укорененное, следует применять программу fdrawgram.
Выполняя обязательные упражнения по деревьям, мы уже визуализровали деревья с помощью этой программы (см.
здесь, самые последние изображения). При этом мы, чтобы получить фенограмму,
ориентированную листьями вправо, не использовали никаких дополнительных параметров программы. И в данном случае мы,
введя в командную строку следующее:fdrawgram -nj_rooted.treefile -auto |
|
С помощью метода максимального правдоподобия можно не только выяснять родство изучаемых последовательностей и строить деревья, но и восстанавливать последовательность гипотетического предка. При желании, построив дерево, можно потом приписать каждому его узлу и корню некую последовательность, восстановив ее на основании имеющихся последовательностей. Мы знаем реальные последовательности, находящиеся в каждом узле и корне нашего дерева; дерево, построенное с помощью fdnaml, совпало с реальным, и поэтому у нас появляется еще одна возможность: сравнить восстановленные методом максимального правдоподобия последовательности с реальными.
Будем обозначать предковую последовательность для для С,В и E - как CDE, и т.п. Методом максимального правдоподобия получим последовательности корня и всех узлов дерева. Для этого сделаем следующее:
-
Скопируем файл ABCDEF.fasta, содержащий все изучаемые мутантные последовательности, в отдельную папку.
+--------------B | | +----------------------------------F | | 1--------------4 +-------E | | +------3 | +-------------2 +---------D | | | +---------C | +--------AВот схематически изображенное реальное укорененное дерево:
+----------------------------------------F
!
! +------------C
--1 +---------------------3
! ! ! +------D
! ! +--------4
+--2 +------E
!
! +----------A
+--------------------------5
+----------B
А вот укорененное дерево из выходного файла
fdnamlk:+------------------------------------B ! ! +-----------------------------------F ! ! --1--2 +------------E ! ! +-----4 ! +----------------3 +------------D ! ! ! +------------------C ! +------------------------------------AЗдесь получается, что корень - узел 1,из которого выходят узел 2 и листья A и B, то есть дерево небинарное. Это подтверждается данными следующей таблицы, взятой из выходного файла fdnamlk:
Ancestor Node Node Height Length -------- ---- ---- ------ ------ root 1 1 B 0.81427 0.81427 1 2 0.02211 0.02211 2 F 0.81427 0.79216 2 3 0.40449 0.38238 3 4 0.53382 0.12932 4 E 0.81427 0.28045 4 D 0.81427 0.28045 3 C 0.81427 0.40978 1 A 0.81427 0.81427
|
В первой колонке указан "порядок родства", во второй - соответствующие ему узлы. Видно, что корень один, и из него выходят
три ветви первого порядка. Таким образом, корень этого дерева не соответствует полностью корню реального дерева,
если рассматривать его как узел дерева. С другой стороны, по смыслу оба корня означают одно и то же - некую последовательность,
от которой произошли все остальные последовательности, участвующие в построении дерева. Поэтому получим последовательность узла
под номером 1 из выходного документа fdnamlk и сравним с последовательностью гена аspC, которая служила предковой в случае
реального дерева. Сравнивать будем путем обычного глобального выравнивания, воспользовавшись программой needle.
Чтобы в последовательности не вставлялись гэпы (наша модель эволюции поддерживает только замены, но не делеции и вставки),
зададим максимальные штрафы за открытие (100) и продолжение (10) гэпа.
Выравнивание можно увидеть здесь. Величины Identity (58.2%) и
Similarity (65.7%)
не маленькие, но и не самые большие; это можно объяснить тем, что в последовательности, восстановленной с помощью fdnamlk
есть не только буквы "a,t,g,c", но и консенсусные обозначения (к примеру, s,w), с которыми needle работать не "умеет". Думается,
на самом деле соответствие между реальной предковой и реконструированной в виде консенсуса последовательностями еще больше.
В дереве из выходного файла fdnamlk есть два узла, полностью соответствующие узлам реального дерева: CDE и DE. Думается, сравнение последовательностей, относящихся к этим узлам (реальной и реконструированной) будет особенно интересным. Получим последовательности, соответствующие этим узлам, из выходного файла fdnamlk с помощью "grep" и построим глобальное выравнивание, как было описано выше. Для случая с CDE выравнивание можно увидеть здесь, в случае c DE - здесь. |
|
Итак, мы получили гипотетические последовательности, соответствующие узлам дерева различного уровня - корню (наиболее удаленному от последовательностей A-F узлу), узлу CDE и узлу, объединяющему всего две последовательности D и E. Эти последовательности мы сравнили с помощью needle с реальными последовательностями, находящимися в корне и в узлах CDE и DE. Ниже приведена таблица, в которой указаны Identity и Similarity соответствующих выравниваний.
| Узел | Identity,% | Similarity,% |
| Корень | 58,2 | 65,7 |
| СDE | 75,3 | 81,5 |
| DE | 82,0 | 87,5 |
Чем меньше последовательностей, на основании которых восстанавливалась гипотетическая последовательность, тем выше ее соответствие с реальной. Это понятно, поскольку "корневая" последовательность восстанавливалась с использованием шести последовательностей, а последовательность из узла DE - только двух. Мутанты D и E произошли от одной последовательности, каждая отличается от нее одним и тем же числом замен. В такой ситуации еще достаточно легко восстановить ход событий и написать консенсус, в целом совпадающий с реальным предком. Но если было много ступеней "эволюции", на каждой из которых были замены, восстановить предка становится сложнее, и чем больше таких ступеней, тем дальше консенсус от реальности, тем больше в нем условных консенсусных обозначений. Заметим, что указанная зависимость почти линейная (см. здесь)
©Ганчарова Ольга