Реконструкция филогении (доп. задания)
7*. Поиск диагностических позиций выравнивания
Для выполнения дополнительных заданий было взято выравнивание
из 4 задания предыдущего
практикума:
task_2_alignment.fasta.
В полученном выравнивании я попыталась найти диагностические позиции, т.е. позиции,
консервативные для какого-либо из таксонов. На рис. 1-4 приведены некоторые примеры
с пояснениями.
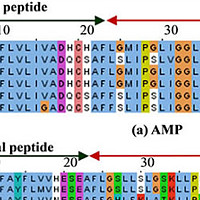
 Рис. 1. В качестве
первого примера была взята позиция 3. На рисунке видно, что в последовательностях
белка бактерий из таксона Clostridia (выделены серым) в данной позиции (выделена
красным) стоит фенилаланин (гидрофобная, ароматическая, незаряженная аминокислота),
в то время как у всех остальных — лизин (положительно заряженная, гидрофильная
аминокислота). Рис. 1. В качестве
первого примера была взята позиция 3. На рисунке видно, что в последовательностях
белка бактерий из таксона Clostridia (выделены серым) в данной позиции (выделена
красным) стоит фенилаланин (гидрофобная, ароматическая, незаряженная аминокислота),
в то время как у всех остальных — лизин (положительно заряженная, гидрофильная
аминокислота). |
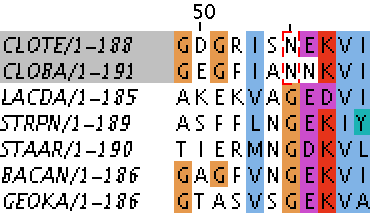 Рис. 2. Второй пример опять для
выделения того же таксона, но на этот раз диагностическая позиция 55, в которой в
последовательностях у бактерий из класса Clostridia стоит аспарагин, а у остальных
— глицин. Рис. 2. Второй пример опять для
выделения того же таксона, но на этот раз диагностическая позиция 55, в которой в
последовательностях у бактерий из класса Clostridia стоит аспарагин, а у остальных
— глицин. |
 Рис. 3. Третий пример —
позиция 87, в которой в последовательностях белков бактерий из класса Clostridia
стоит аспарагин (незаряженная аминокислота), а у всех остальных — аспартат
(отрицательно заряженная аминокислота). Рис. 3. Третий пример —
позиция 87, в которой в последовательностях белков бактерий из класса Clostridia
стоит аспарагин (незаряженная аминокислота), а у всех остальных — аспартат
(отрицательно заряженная аминокислота). |
 Рис. 4. Последний пример посвящен
отряду Lactobaciliales. В позиции 69 в последовательностях у бактерий этого таксона
стоит глутамат (отрицательно заряженная, гидрофильная аминокислота), у остальных
— лейцин (незаряженная, гидрофобная аминокислота). Рис. 4. Последний пример посвящен
отряду Lactobaciliales. В позиции 69 в последовательностях у бактерий этого таксона
стоит глутамат (отрицательно заряженная, гидрофильная аминокислота), у остальных
— лейцин (незаряженная, гидрофобная аминокислота). |
Из примеров, представленных на рис. 1-4, видно, что часто в диагностических позициях
у разных таксонов находятся аминокислоты, сильно различающиеся по свойствам. Если они
входят в активный центр, то отличие в свойствах может приводить и к изменению
функциональности того или иного центра. Кроме того, кодоны, кодирующие соответствующие
аминокислоты, сильно различаются, что также говорит о небольшой вероятности замен этих
аминокислот.
К сожалению, я не нашла много разных примеров диагностических позиций. Большая часть
позволяла выделить именно класс Clostridia (ну или класс Bacilli, как больше нравится).
Хочу заметить, в качестве диагностических позиций я не брала такие, в которых у одного
таксона у всех бактерий в последовательностях одна и та же аминокислота, а в других
таксонах — разные (т.е. неконсервативные для таксона позиции).
Каких-то инделей, характерных определенному таксону, найдено тоже не было. Думаю,
это объясняется выбором белка; возможно, аминокислотные замены в нем не приводят к
серьезным нарушениям его функций, а следовательно не отбраковываются отбором.
8*. Сравнение работы алгоритма NJ при разных способах построения матрицы расстояний
В этом задании необходимо было сравнить деревья, построенные
Jalview с помощью
разных способов построения матрицы расстояний. Всего используется три
1:
- PID (percentage identity): подсчёт процента совпадающих букв.
Буквально, число консервативных позиций на сто аминокислотных остатков;
- BLOSUM62: подсчёт весов сопоставлений (по матрице
BLOSUM62);
- PAM250: подсчёт весов сопоставлений (по матрице
PAM250).
Прим. В документации также упоминается
Sequence Feature Similarity,
однако в этом случае строилось не нормальное дерево, а прямая с отмеченными отрезками.
Интересно, почему.
Итак, было построено три дерева, изображенных на рис. 5-7.
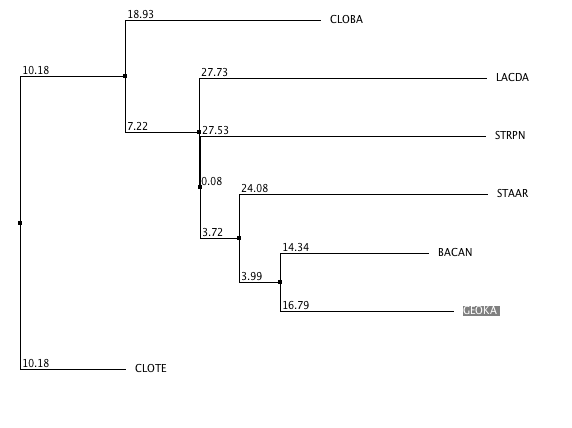 Рис. 5.
Дерево, построенное при подсчете совпадающих позиций
(PID) Рис. 5.
Дерево, построенное при подсчете совпадающих позиций
(PID) |
В первом случае дерево имеет три верные нетривиальные ветви
(см. задание 1
предыдущего практикума):
- {CLOBA, CLOTE} vs {LACDA, STRPN, BACAN, GEOKA, STAAR};
- {CLOBA, CLOTE, LACDA} vs {STRPN, BACAN, GEOKA, STAAR};
- {CLOBA, CLOTE, LACDA, STRPN} vs {BACAN, GEOKA, STAAR};
- {BACAN, GEOKA} vs {STAAR, CLOBA, CLOTE, LACDA, STRPN}
Таким образом, как уже говорилось в задании 4 предыдущего практикума, все ветви, кроме
второй совпадают. Вторая же ветвь разделяет виды на две группы, в состав каждой из которых
входят представители разных классов. Тем не менее, результат лучше, чем я ожидала при
таком сомнительном способе построения матрицы расстояний.
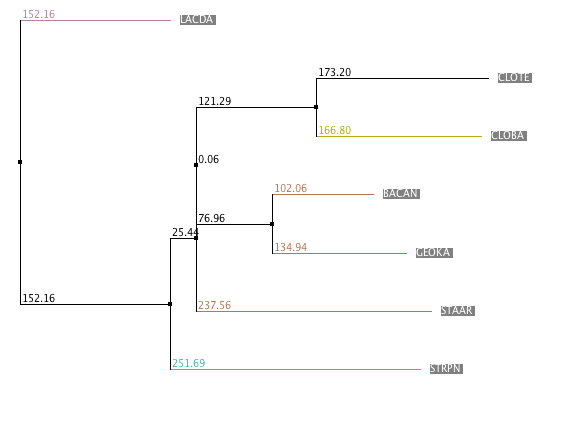 Рис. 6.
Дерево, построенное по матрице весов (PAM250) Рис. 6.
Дерево, построенное по матрице весов (PAM250) |
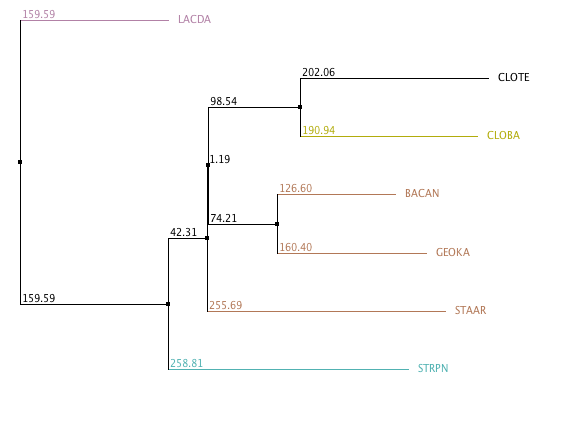 Рис. 7.
Дерево, построенное по матрице весов (BLOSUM62) Рис. 7.
Дерево, построенное по матрице весов (BLOSUM62) |
Следующие два дерева лишь немного отличаются длинами ветвей, и при этом имеют
одинаковую топологию (хотя одна ветвь на рис. 6 слабо различима, т.к. имеет длину
0.06). Это неудивительно, так как способ построения матриц расстояний
в обоих случаях одинаковый, различаются только матрицы весов. Сравним ветви
с реальными:
- {CLOBA, CLOTE} vs {LACDA, STRPN, BACAN, GEOKA, STAAR};
- {LACDA, STRPN} vs {CLOBA, CLOTE, BACAN, GEOKA, STAAR};
- {BACAN, GEOKA} vs {STAAR, CLOBA, CLOTE, LACDA, STRPN};
- {CLOTE, CLOBA, BACAN, GEOKA} vs {LACDA, STRPN, STAAR}
Первые три нетривиальные ветви есть в реальном дереве видов, а последняя разделила
группы, в составе которых представители разных таксонов. Таким образом, эти два
способа оценки расстояний из-за своей примитивности приводят к неверным результатам.
Сравним с этими тремя деревьями дерево, построенное
MEGA тем же методом, но
при другом подсчете расстояний (принцип максимального правдоподобия).
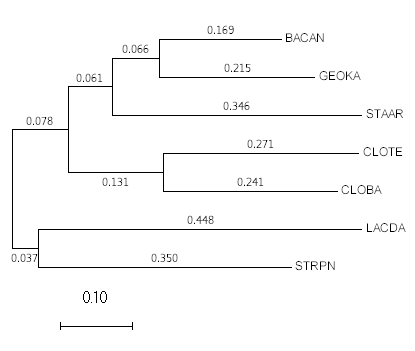 Рис. 8.
Дерево, построенное в MEGA с помощью матрицы расстояний, Рис. 8.
Дерево, построенное в MEGA с помощью матрицы расстояний,
построенной основываясь на принципе максимального правдоподобия. |
Нетривиальные ветви в данном случае следующие:
- {BACAN, GEOKA} vs {STAAR, CLOBA, CLOTE, LACDA, STRPN};
- {BACAN, GEOKA, STAAR} vs {CLOBA, CLOTE, LACDA, STRPN};
- {CLOBA, CLOTE} vs {LACDA, STRPN, BACAN, GEOKA, STAAR};
- {LACDA, STRPN} vs {CLOBA, CLOTE, BACAN, GEOKA, STAAR}.
Благодаря усовершенствованному способу оценки расстояний в этом случае
все ветви верные и дерево построено правильно.
Выводы: при построении дерева методом Neighbor-joining
Jalview
использует несовершенные способы оценки расстояний, в связи с чем были построены
неправильные деревья. Программа
MEGA при том же методе построения ошибок не
допустила, так как в этом случае использовался другой способ построения матрицы
расстояний. Тем не менее, так как филогенетические деревья строятся при анализе
выравниваний большого числа белков, разные методы и разные программы могут быть
полезны в разных случаях.