Для парного глобального и локального выравниваний мы используем, соответственно, программы needle и water пакета EMBOSS. Эти программы получают на вход последовательности в формате fasta и выдают (по умолчанию) файлы формата .needle или .water. Однако программа JalView (которая их визуализирует) воспринимает файлы иного формата, например формата .fasta, что толкает нас на использование опции -aformat fasta, чтобы изменить выходной файл под наши нужды. Cравнение выравниваний проводилось на следующих гомологичных белках (взятых из предыдущего практикума):
| Entry | Entry name | Protein names | Length | Superkingdom | Organism |
| Q82EX9 | DNAK1_STRAW | Chaperone protein dnaK1 (HSP70-1) | 622 | Bacteria | Streptomyces avermitilis (strain ATCC 31267 / DSM 46492 / JCM 5070 / NBRC 14893 / NCIMB 12804 / NRRL 8165 / MA-4680) |
| A1T2S3 | DNAK_MYCVP | Chaperone protein DnaK (HSP70) | 622 | Bacteria | Mycobacterium vanbaalenii (strain DSM 7251 / PYR-1) |
Таблица 1. Рассматриваемые белки.
Следует отметить, что некоторые параметры вывода заданы по умолчанию, однако во входе программы их можно изменить (в случае, если они не указаны, программа может попросить их на дополнительный ввод.) Штрафы за открытие инделя, за удлиннение и за последний гэп задаются, соответственно, для needle/water атрибутами -endopen/-gapopen; -endextend/-gapextend; -endweight (в needle). По умолчанию ( и в нашем случае) штраф за открытие инделя равен 10.0 у.е, штраф за удлиннение - 0.5, штраф за последний гэп отсутствует. Матрица весов задается атрибутом -datafile и для белка это EBLOSUM62, для ДНК - EDNAFULL
На данном этапе работы хотелось бы пояснить отличие между глобальным и локальным выравниванием:
Глобальное выравнивание представляет из себя сравнение последовательностей целиком, по всей длине, не игнорируя ни единой буквы.
Локальное выравнивание отличается тем, что позволяет опустить штраф за начало и конец последовательности.
Локальное выравнивание в большинстве своём учитывает более консервативные гомологичные учатски для более точных результатов.
Очевидно, что выход этих двух выравниваний может различаться, так как во втором случае части последовательности просто напросто могут отсутствовать.
Напротив, в первом случае эти буквы могут быть задействованы в той или иной гомологии в последовательностях.
В таблицах ниже представлены данные для двух выравниваний Используя опцию Tcoffee with Defaults, было смоделированоы визуализации выравниваний последовательностей белков с раскраской по схеме ClustalX, при Identity Threshold = 100%. Часть выравнивания выступает ссылкой на полное выравнивание (чтобы его открыть, нужно нажать на соответсвующую картинку). ter (как и в предыдущем практикуме для того, чтобы увидеть выравнивание целиком, надо нажать на картинку с его фрагментом). Длина гэпов должна соответствовать числу инделей, потому что пропуск одной буквы в гэпе первой последовательности соответствует отсутствию гомологии в другой последовательности. То есть либо в одной из последовательностей могла произойти либо делеция, либо вставка.
| Name | Sequence Length | Aligned Length | Number of Gaps | Gap Length | % | Identity | Similar | % |
|---|---|---|---|---|---|---|---|---|
| DNAK_MYCVP | 622 | 630 | 2 | 8 | 1,2 | 458 | 0 | 72,7 |
| DNAK_MYCVP | 622 | 634 | 3 | 12 | 1,9 | 458 | 0 | 72,24 |
| DNAK1_STRAW | 622 | 634 | 5 | 12 | 1,9 | 458 | 0 | 72,24 |
| Выравнивание | 622 | 634 | 4 | 10 | 1,6 | 458 | 0 | 72,24 |
Таблица 2. Глобальное выравнивание, Identity 100%
Стоит отметить, что в данной таблице представлена выдача программы, а та игнорирует 4 последних гэпа у DNAK_MYCVP.
| Name | Sequence Length | Aligned Length | Number of Gaps | Gap Length | % | Identity | Similar | % |
|---|---|---|---|---|---|---|---|---|
| DNAK_MYCVP | 622 | 630 | 2 | 8 | 1,2 | 534 | 0 | 84,8 |
| DNAK_MYCVP | 622 | 634 | 3 | 12 | 1,9 | 534 | 0 | 84,2 |
| DNAK1_STRAW | 622 | 634 | 5 | 12 | 1,9 | 458 | 76 | 84,8 |
| Выравнивание | 622 | 634 | 4 | 10 | 1,6 | 534 | 0 | 84,8 |
Таблица 3. Глобальное выравнивание, Plurality 100%
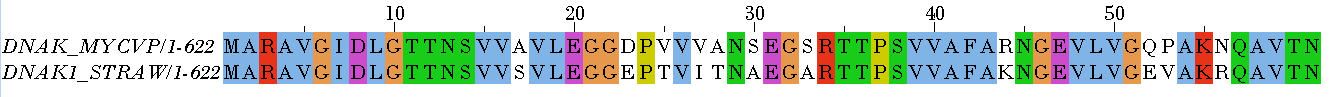Рисунок 1. Глобальное выравнивание
| Name | Sequence Length | Aligned Length | Number of Gaps | Gap Length | % | Identity | Similar | % |
|---|---|---|---|---|---|---|---|---|
| DNAK_MYCVP | 620 | 628 | 2 | 8 | 1,27 | 456 | 0 | 72,6 |
| DNAK1_STRAW | 618 | 628 | 4 | 10 | 1,6 | 456 | 0 | 72,6 |
| Выравнивание | 622 | 628 | 3 | 9 | 1,44 | 456 | 0 | 72,6 |
Таблица 4. Локальное выравнивание, Identity 100%
| Name | Sequence Length | Aligned Length | Number of Gaps | Gap Length | % | Identity | Similar | % |
|---|---|---|---|---|---|---|---|---|
| DNAK_MYCVP | 620 | 628 | 2 | 8 | 1,27 | 534 | 0 | 84,8 |
| DNAK1_STRAW | 618 | 628 | 4 | 10 | 1,6 | 456 | 78 | 84,8 |
| Выравнивание | 622 | 628 | 3 | 9 | 1,44 | 534 | 0 | 84,8 |
Таблица 5. Локальное выравнивание, Plurality 100%
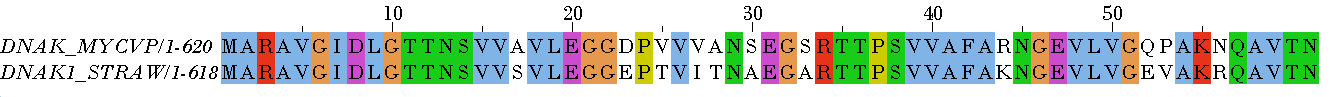Рисунок 2. Локальное парное выравнивание
В данном задании были использованы ранее выданные группе негомологичные белки, идентификаторы являются ссылками на страницу студентов, которые ранее работали с этими белками:
| ID | Protein names | Length |
|---|---|---|
| AFH91336.1 | 4-alpha-glucanotransferase | 729 |
| AHB99924.1 | CRISPR-associated protein Csn1 | 1269 |
| ALV01889.1 | Polyketide synthase | 2094 |
| AML53752.1 | Mercuric reductase | 477 |
| ANI03399.1 | Nitrile Hydratase subunit beta | 220 |
| BAC73082.1 | Putative globin-like protein | 134 |
Таблица 6. Используемые белки.
В ходе выравнивания гомологичных и негомологичных последовательностей можно заметить несколько закономерных отличий данных двух случаев:
| Name | Sequence Length | % | Aligned Length | % | Gaps | Gap Length | % | Identity | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| identity 100% | % | plurality 100% | % | ||||||||
| AFH91336.1 | 80 | 10,98 | 89 | 12,21 | 3 | 9 | 10,11 | 23 | 25,84 | 44 | 49,44 |
| AHB99924.1 | 84 | 6,62 | 7,01 | 2 | 5 | 5,62 | |||||
| AFH91336.1 | 700 | 96 | 861 | 118,1 | 22 | 161 | 18,7 | 164 | 19 | 257 | 29,85 |
| ALV01889.1 | 698 | 33,3 | 41,12 | 25 | 163 | 19 | |||||
| AFH91336.1 | 261 | 35,8 | 331 | 45,4 | 14 | 70 | 21,14 | 77 | 23,26 | 106 | 2 |
| AML53752.1 | 296 | 62,05 | 69,4 | 6 | 35 | 10,57 | |||||
| AFH91336.1 | 126 | 7,3 | 140 | 19,2 | 3 | 14 | 10 | 39 | 27,9 | 52 | 37 |
| ANI03399.1 | 120 | 54,5 | 63,6 | 7 | 20 | 14,3 | |||||
| AFH91336.1 | 89 | 12,2 | 96 | 13,2 | 2 | 7 | 1 | 27 | 28 | 36 | 37,5 |
| BAC73082.1 | 72 | 53,7 | 71,6 | 7 | 24 | 25 | |||||
Таблица 7. Выравнивания негомологичных белков.
Ниже приведены ссылки на соответствующие попарные выравнивания, каждая даёт ссылку на такое же, но полное:
Ниже приведены три типа выравниваний: парное взятое из множественного выравнивания с последовательностями из предыдущего задания, локальное парное и глобальное парное.
В качестве рассматриваемых объектов была взята последняя пара из предыдущего задания:
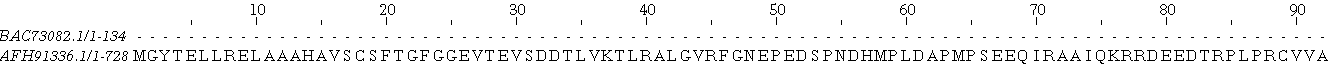
Невооружённым взглядом видно, что выравнивания не одинаковы: есть различия в началах выравниваний, причём во всех трёх, у локального нет начала, а глобальное сдвинуто относительно части множественного, так как в каждом случае выбран оптимальный вариант, и, видимо, том случае имело смысл начинать с начала последовательностей. К тому же сильно различаются длины выравниваний: в 'соместном проекте', где загружены все три выравнивания, это хорошо видно. Конечно же, позиции некоторых аминокислот изменены. Например, связка глутамат-аспартат-лизин-глицин во множественном выравнивании сохраняется только в одной последовательности начиная с 604 остатка и её пересекает гэп, в локальном выравнивании открывает выравнивание, когда как в глобальном выравнивании приходится на гэп с 525 на 528 номер остатка.(синим обозначены гэпы)
 |
 |
Та же самая история наблюдается с меняющими своё положение гэпами: например, во множественном выравнивании первых гэпов нет, парное же глобальное выдаёт нам вариант, что последовательность сдвинута относительно другой, и её начало мы видим лишь на 618 остатке наибольшей:
 |
В целом, в данном случае не слишком многое можно сказать на счёт актуальности какого-либо из выравниваний, так как они построены с негомологичными белками. Скорее уж тем больше негомологов мы возьмём, тем менее вероятное выравнивание получим.
Рассмотрим теперь гомологи: логично предположить, что чем больше гомологичных белков мы сравниваем, тем актуальнее будет выравнивание, ведт мы предоставляем программе более точное расположение,
меньше прав на ошибку.
Возьмём множественное выравнивание из предыдущего практикума и построим дополнительно глобальное и локальное:
 |
Постараемся найти аналогию, способную описать построения глобальное выравнивания:
Представим себе Венецию эпохи Медичи, где весь город представляет из себя систему островов и каналов.
Все острова - отдельные прямоугольники, границы между ними - каналы. Система каналов тянется через весь город. Острова по углам соеденены мостами. По ним передвигаться
проще, чем по воде.
Некий человек стремится пересечь город как можно быстрее, допустим, он спешит к своей возлюбленной, которую суровые родители увезли от него на другой конец города,
а именно, на юго-восток. Он знает, что двигаться ему тогда из северо-западного угла нужно только на восток/юг/юго-восток.
Естветсвенно, наш герой способен путешествовать как по воде, так и по суше, однако по воде перевозить его могут лишь гондольеры.
Ему нужно расчитать оптимальный путь, чтобы скорее пересечь город. Используется для этого особая система счёта: замедлиться герой может из-за усталости или длительности пути, это выражается в потере очков времени, если же он ускорится, то приобретёт их.
Есть два пути: всегда идти по суше через узкие мостки островов или пользоваться гондолами. На суше он может встретить тех, кто поможет ему быстрее добраться до девушки(добрые городжане = плюс-баллы) и тех, кто замедлит его (злые горожане = минус-баллы). Гондольеры же плывут медленнее, чем герой движется по суше - то есть он теряет время с ними (минус-баллы). Однако обычно не так много, как при стычке со злыми горожанами на суше. У каждого мостка, читай, угла острова, нужно вновь выбирать направление и способ передвижения, что тоже тратит его время, потерю этих баллов времени можно рассматривать как штраф. Чтобы не углубляться в сложные материи, будем считать, что потеря баллов за смену гондольера (смену направления) и из-за перехода с суши на гондолу приблизетельно одинакова.
Получается, что острова герой всегда пересекает лишь по диагонали потому что торопится, а по воде движется в двух оптимальных направлениях. На суше он может как потерят баллы в своей системе счёта, так и приобрести, путешествие с гондольером всегда лишает его баллов, но меньших, чем при столкновении с противником на суше. Баллы так же тратятся при переходе на гондолу и возвращении с гондолы на сушу. А добраться до возлюбленной нужно с максимальной суммой баллоы - это будет означать, что он придёт как можно скорее. Иными словами, герой строит выравнивание двух последовательностей каналов, что и означает глобальное выравнивание в нашем случае.
В нашей аналогии баллы за путь по суше = баллы за замену = вес ребра в матрице. Штраф за гэп = баллы, потраченные на гондольеров. Смена средства передвижения, будь то гондола на гондолу или гондола на собственые ноги и наоборот = штраф за начало гэпа, который больше, чем за продолжение гэпа, потому что продолжительный гэп более вероятен, чем много непродолжительных.
Теперь рассмотрим другой вариант развития событий. Допустим, теперь герой располагает деньгами. Его цель - добраться к пункту заключения договора (на юго-восточный угол карты) с ценными бумагами как можно быстрее. По правилу "время-деньги" он теряет монеты если медлит (допустим, получает штраф за опоздание при заключении сделки) или если расплачивается с кем-то по пути. В точку назначения ему, как и любому дельцу, хочется попасть, имея на руках максимальное количество монет. Иными словами, пересечь карту с северо-запада на юго-восток.
Под каждым мостком на углах островов-клеток затаился "недоброжелатель" из прошлого примера. Теперь их цель - отобрать деньги. Враги расположены так, что путешествуя на гондоле(то есть строго на юг или строго на восток), неизменно натыкаешься на них под мостом. Но если путешествовать по суше, то можно напасть с тыла. Обычно такая стычка обходится ему дороже, чем просто-напросто отдать деньги на воде, потому он будет стараться их избегать. Но участвовать в них придётся - это дело чести. И в некоторых случаях за стычку он может приобрести монеты.
Ещё осталось пара моментов, которые отличают ситуацию от предыдущего примера.
Во-первых, изначально путешествие может начаться из любой точки карты, герой может выбрать, откуда он начнёт, и этот путь считает нейтральным, потому как
его безопастность,обеспечивает заказчик, который предоставляет ему экипаж (эта особенность отражает локальное выравнивание, которое может начаться
не с начала последовательности. То есть штраф за начальные гэпы будет равен нулю).
Кроме того, можно договориться о том, что всадники подберут героя на каком-то из мостков и доставят до пункта наначения. Получается,
что у него есть возможность попасть первым шагом на любой мост и с любого моста в пункт назначения. Но часть пути ему всё равно нужно проделать самому,
чтобы не привлечь внимания и сделка не сорвалась, то есть сумма весов каналов пути будет обязательно больше нуля.
Итого: по сравнению с предыдущим случаем, герой имеет возможность срезать начало и конец, не потеряв деньги, штраф за гэпы линеен, то есть ребро каждого "острова" имеет одинаковый вес (потому как он устаёт совершенно одинаковым образом). Как и в предыдущем задании, герою нужно построить выравнивание карте, путь, узлами которого станут мосты с врагами, а пересечение островов по суше будет соответствовать заменам из одной последовательности в другой. Вес рёбер - количество монет, которые герой потеряет или приобретёт в ходе встречи со врагами. Если переход по суше соответствует замене, то канал между двумя островами это индель, то есть потеря монет на нём - штраф за индель. А экипаж или всадники - рёбра, соединяющие самый северо-западный угол карты (начало пути) и самый юго-восточный (конец пути) со всеми мостками, что позволяет герою сократить путь.
21.04.17 состоялся концерт Национального филармонического оркестра России, который удалось посетить Веселовой Софье, после чего она любезно предоставила нам материалы для дальнейшей работы.
Ниже представлена схема рассадки зала, построенная после анализа фотографии:
 |
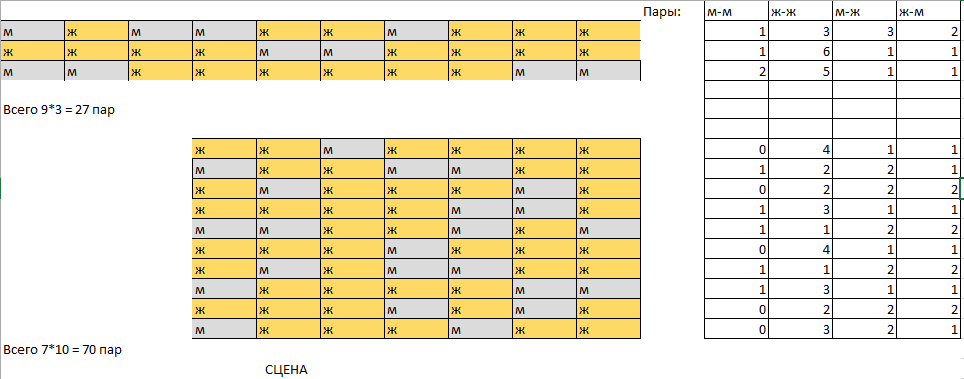Часть мест расположена была перпендикулярно основным рядам, эти боковые места вынесены отдельно.
Далее, следует посчитать пары мест: очевидно, что в местах партера можно составить 60 пар(по 6 на каждый ряд) и ещё 27 ар дают боковые места (по 9 на три ряда).
Всего мест получает 87. Имеем 33 мужчин и, соответственно, 67 женщин на 100 местах.
Тогда вероятность обнаружить на каком-либо месте мужчину - 0,33, а женщину - 0,67. Обозначим вероятность привычным Р.
Вероятность получить на каких-либо двух местах одновременно пару заданных полов - произведение вероятностей Р.
Полученнное число на число пар - случайное распределение по типам пар. Отношение числа пар одного типа к общему числу пар это так же вероятность
получить пару определённого типа - это отношение правдоподобия, обозначим С (credibility). Для гетеро-пар оно усредняется, потому что разницы, с какой стороны сидит
мужчина или женщина не столь важно. Двоичный логарифм отношения параметра С к квадрату Р это и есть вес. Для удобства умножаем вес на 100.
| Тип пары | Вероятность пары такого типа (Р^2) | Случайное расположение (Р*87) | Реальное расположение | Отношение правдоподобия (С) | Отношение С/Р^2 | Вес (100*log) |
|---|---|---|---|---|---|---|
| М-М | 0,1081 | 9.4047 | 8 | 0,09 | 0,833 | -26,36 |
| Ж-Ж | 0,4489 | 39.0543 | 39 | 0,448 | 0,998 | -0,289 |
| М-Ж | 0,2211 | 19.2357 | 21 | 0,241 | 1,09 | 12,433 |
| Ж-М | 18 | 0,207 |
Далее приведём таблицу с целыми значениями веса, которая и будет служить "матрицей дружелюбности":
| Вес: | М | Ж | Сумма |
|---|---|---|---|
| М | -26 | 12 | -14 |
| Ж | 12 | -0,3 | 11,7 |
| Сумма | -14 | 11,7 |
На главную страницуВернуться назад
©Solonovich Vera,2017