Восстановление функции электронной плотности
Создание модельной функции ЭП в одномерной элементарной ячейке, её разложение на гармоники
Для того чтобы задать одномерную функцию электронной плотности была сформирована модель из двух молекул (3+3), которая представлена на рисунке 1. Обе молекулы линейны, представлены длины связей и подписаны названия атомов. Молекулы находятся на расстоянии 3 ангстрема, что соответствует длине водородной связи, хотя в реальности, понятно, что настоящая водородная связь в такой системе из двух атомов образовываться не будет, поскольку углерод в цианиде, хоть и находится под действием азота, не будет иметь достаточного отрицательного заряда. 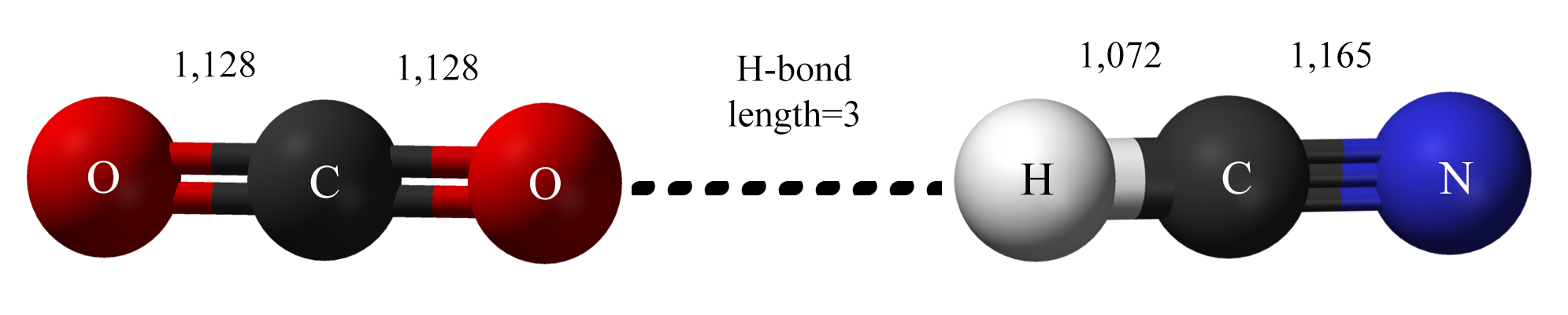 |
Рис. 1 Модель взаимодействия двух молекул, используемая для построения функции электронной плотности. |
На основе данной модели была создана функция, описывающая электронную плотность гауссовыми кривыми, при помощи скрипта compile-func.py со следующими параметрами запуска:
python compile-func.py -g 16,2,5+12,2,6.12+16,2,7.24+2,2,10.24+12,2,11.71+14,2,12.88Вид полученной функции электронной плотности представлен на рисунке 2. По ССЫЛКЕ доступен файл с описанием функции (поточечное описание - для каждой точки на отрезке [0,30] приводится значение функции в точке).
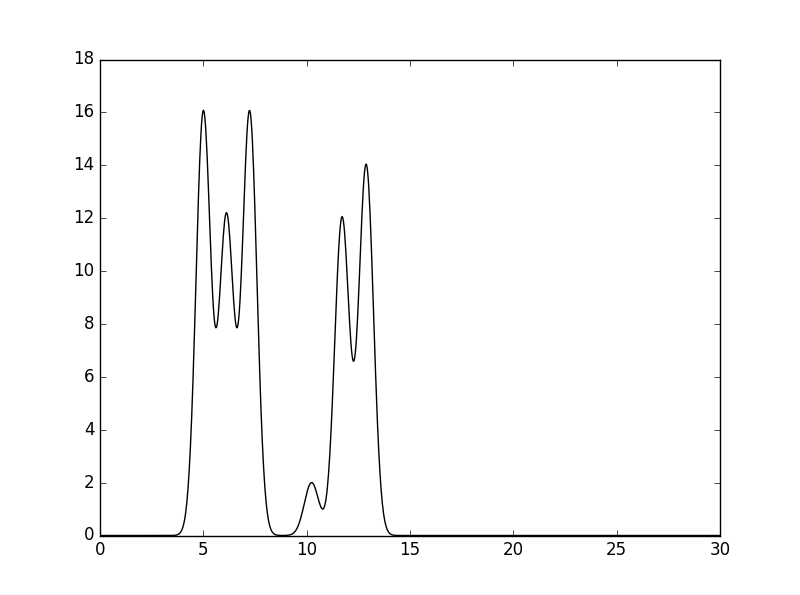 |
Рис. 2 Полученная для рассмотренной модели функция электронной плотности. |
python func2fourier.py -i func.txt -o amplids.txtПолученный файл с параметрами гармоник (амплитуды и фазы) доступен по ССЫЛКЕ.
Восстановление функции электронной плотности по набору гармоник
Сначала была восстановлена исходная функция по полному (499 штук) набору гармоник. Для этого использовался скрипт fourier2func.py с параметрами запуска: python fourier2func.py -i amplids.txt -o func_new_all.txt -s. Как видно из сравнения рисунка 3 (восстановленная функция) и рисунка 2 (исходная построенная функция), функция восстановлена идеально и неотличима от исходной. При использовании полного набора гармоник разрешение составило d=T/n=30/499=0.06 Å. Затем был определён минимальный порог числа гармоник, при котором функция хорошо восстанавливается. Было проведено восстановление функции электронной плотности по 10 (разрешение 3Å), 15(2Å), 20 (1,5Å), 25 (1,2Å) и 32 (0,94Å) гармоникам. Для этого дополнительно использовался скрипт fourier-filter.py, пример запуска скрипта:
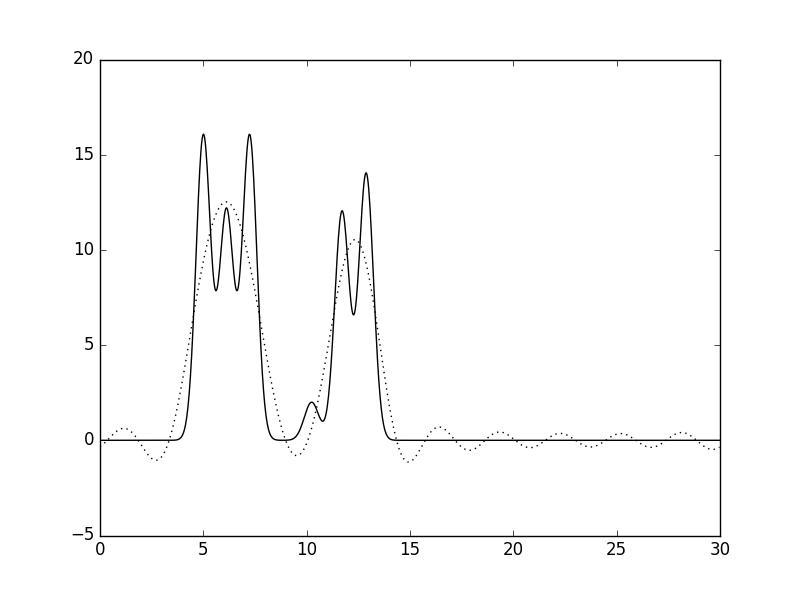
python fourier-filter.py -i amplids.txt -o func_new_20.txt -r 0-20. Результаты представлены на рисунках 4-8. Исходная функция ЭП показана сплошной линией, результат восстановления всюду показан пунктиром. 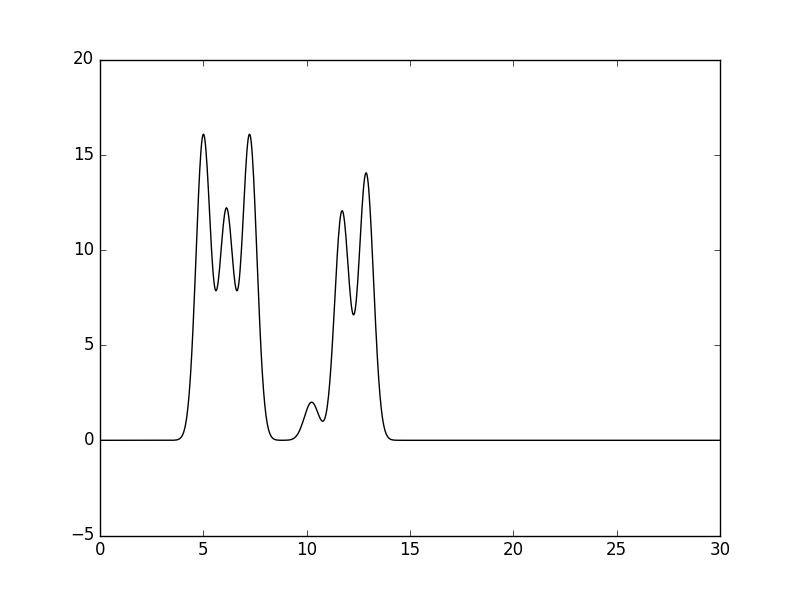 |
 |
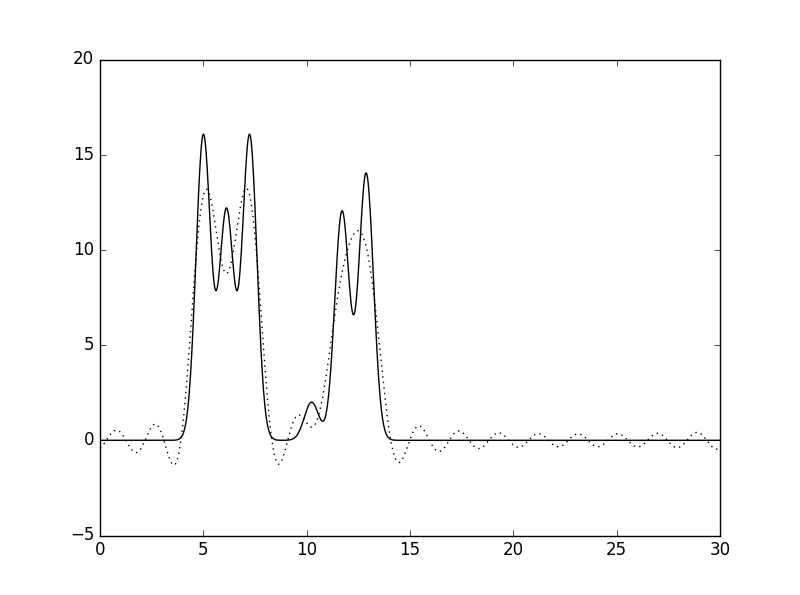 |
Рис. 3 Восстановленная по полному набору гармоник функция ЭП (неотличима от исходной, см. Рис.2). |
Рис. 4 Восстановленная по неполному набору гармоник функция ЭП (n=10, d=3Å). |
Рис. 5 Восстановленная по неполному набору гармоник функция ЭП (n=15, d=2Å). |
 |
 |
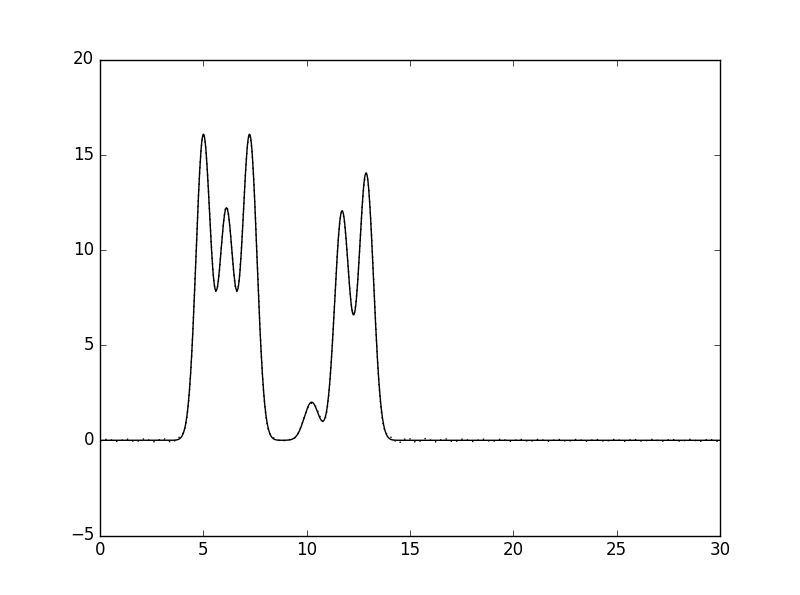 |
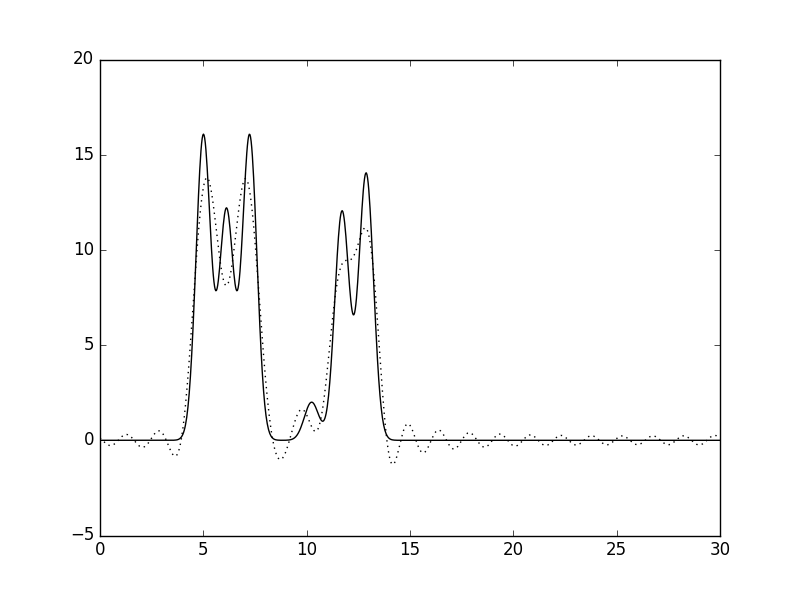
Рис. 6 Восстановленная по неполному набору гармоник функция ЭП (n=20, d=1,5Å). |
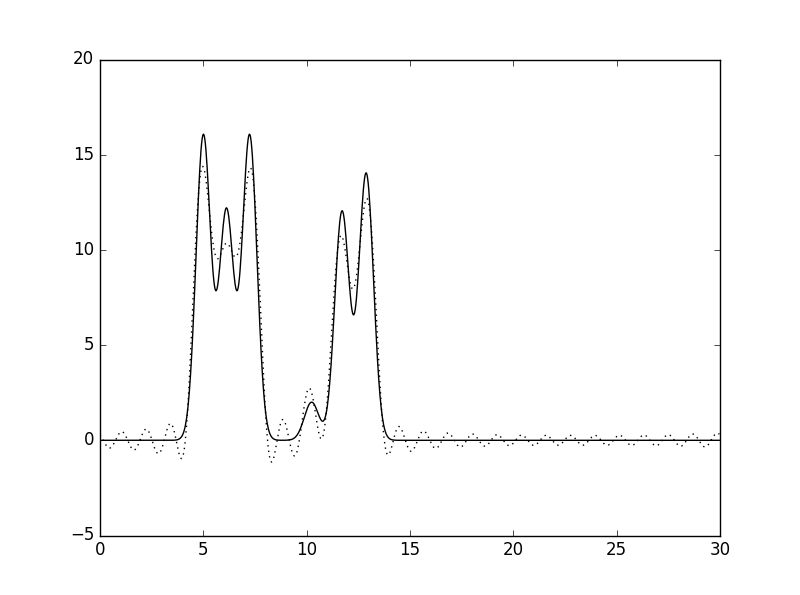
Рис. 7 Восстановленная по неполному набору гармоник функция ЭП (n=25, d=1,2Å). |
Рис. 8 Восстановленная по неполному набору гармоник функция ЭП (n=32, d=0,94Å). |
Влияние шума на восстановление функции электронной плотности
Итак, теперь мы оперируем не со всеми 499-ю гармониками, а только с первыми 32-мя, что соответствует определённому нами ранее n0. Для того чтобы дополнительно приблизить используемую нами модель к условиям реального рентгеновского эксперимента, был введён шум: в скрипте func2fourier.py, который, напомню, создаёт набор гармоник, были выставлены ненулевые значения параметров -F (включение случайного и "нормально распределённого" шума в значения амплитуд) и -P (аналогично для фаз гармоник). Результаты восстановления функции ЭП по гармоникам с включением шума приведены на рисунках 9-11.Пример последовательного запуска скриптов: разложение на гармоники с добавлением шума → отбор 32-х гармоник → восстановление по отобранным гармоникам и сравнение с исходной функцией:
python func2fourier.py -i func.txt -o amplids_mist.txt -F 40 -P 0
python fourier-filter.py -i amplids_mist.txt -o amplids_32_mist.txt -r 0-32
python fourier2func.py -f func.txt -i amplids_32_mist.txt -o func_new_32_mist.txt 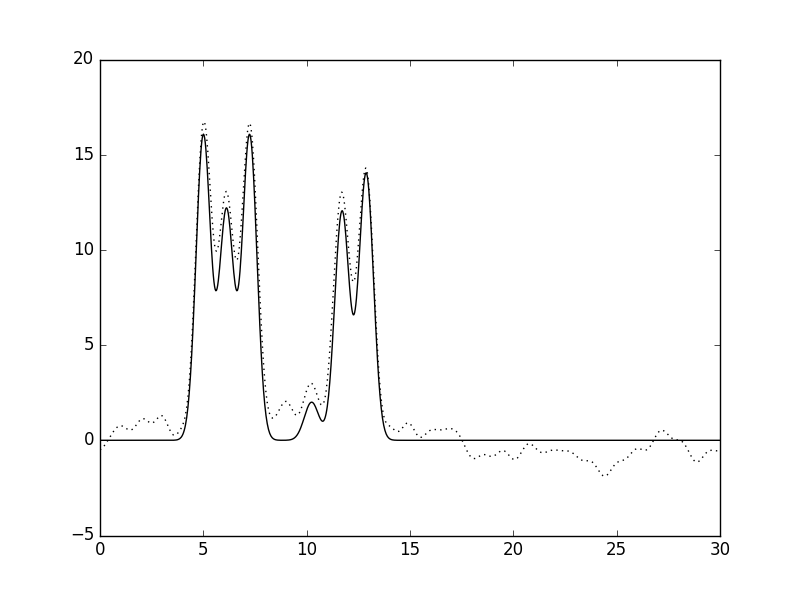 |
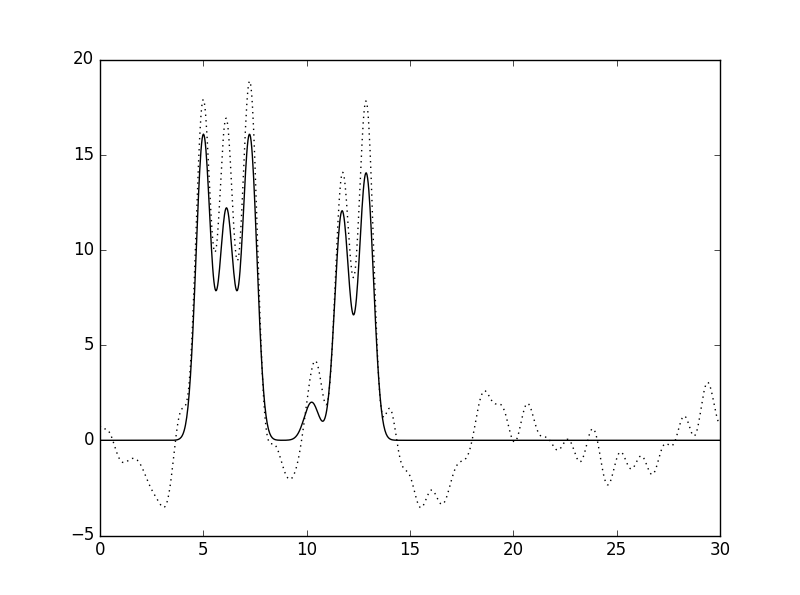 |
Рис. 9 Влияние внесения шума в значения амплитуд гармоник: (F=20, P=0, слева) и (F=40, P=0, справа). |
|
 |
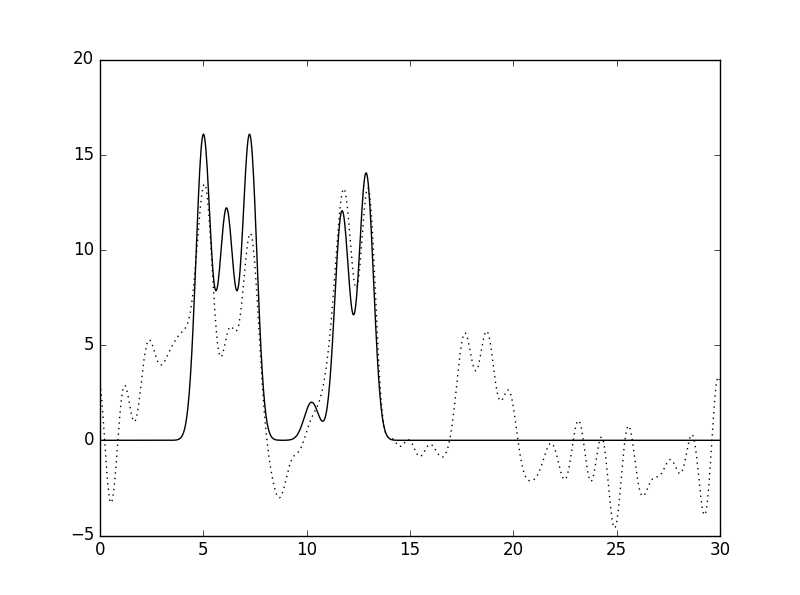 |
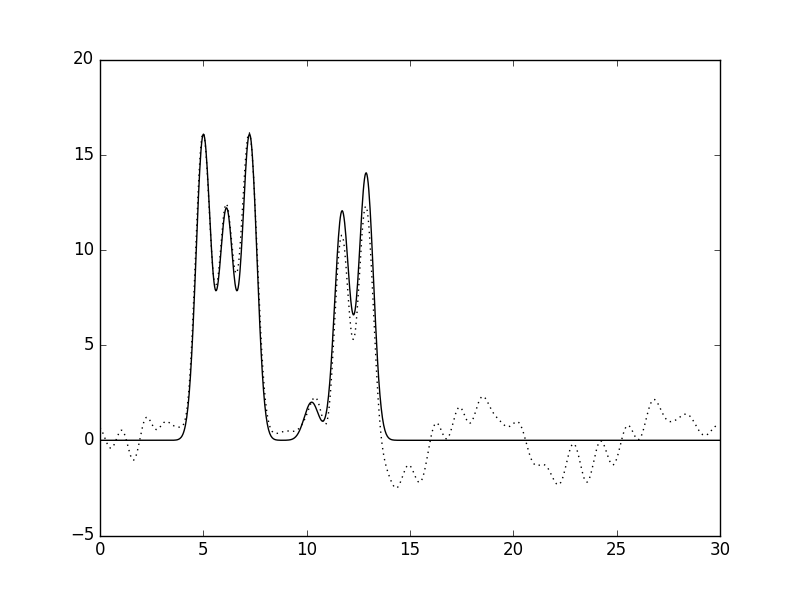
Рис. 10 Влияние внесения шума в значения фаз гармоник: (F=0, P=20, слева) и (F=0, P=40, справа). |
|
 |
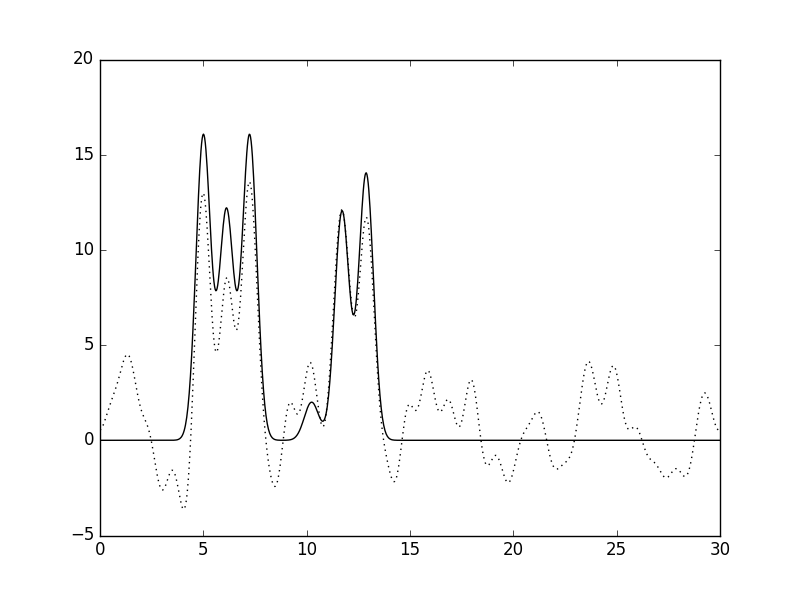 |
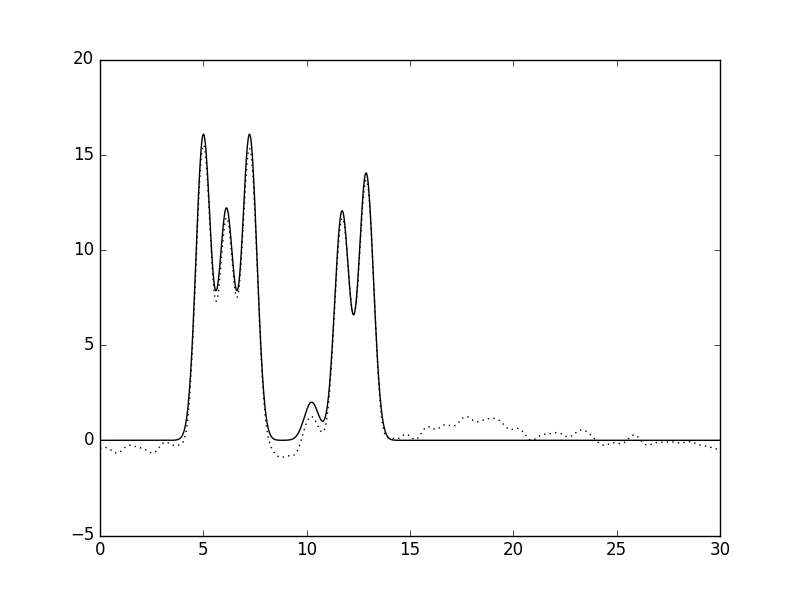
Рис. 11 Суммарное влияние внесения шума и в значения амплитуд, и в значения фаз: (F=5, P=5, слева) и (F=30, P=30, справа) |
|
Из приведённых выше рисунков становится видно, что внесение шума (тех же 40%) в значения фаз (Рис. 10, справа) более критично сказывается на восстановлении функции ЭП, чем в значения амплитуд (Рис. 9, справа). Кроме того, должен отметить, что при внесении небольшого шума (5%) и в фазы, и в амплитуды восстановление функции ЭП можно назвать почти отличным (Рис. 11, слева).
Восстановление функции ЭП по неполному набору гармоник
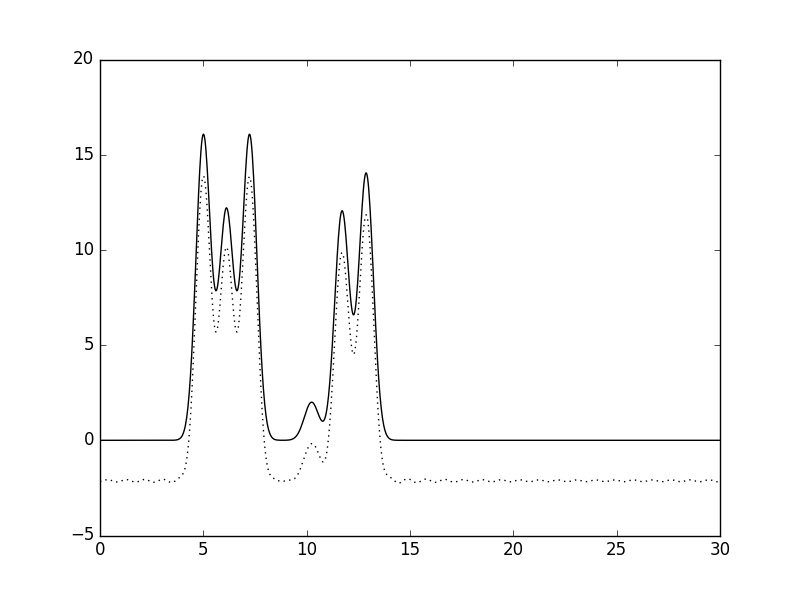
Как мы хорошо знаем, в реальности не всегда удаётся определить все гармоники, такой набор будет называться неполным. Чтобы сымитировать эту ситуацию в нашей модели мы будем удалять и добавлять гармоники в различных "частях" набора.1). На рисунке 12 показаны результаты восстановления функции ЭП по неполному набору гармоник, где из полного набора была удалена первая (Рис. 12, слева) и первые две (Рис. 12, справа) гармоники. видно, что изменения не очень принципиально сказываются на функции ЭП, в первом случае она просто опускается симметрично вниз, во втором же изменения более принципиальны, но все пики остаются хорошо различимыми и качество восстановления можно охарактеризовать как "отличное".
 |
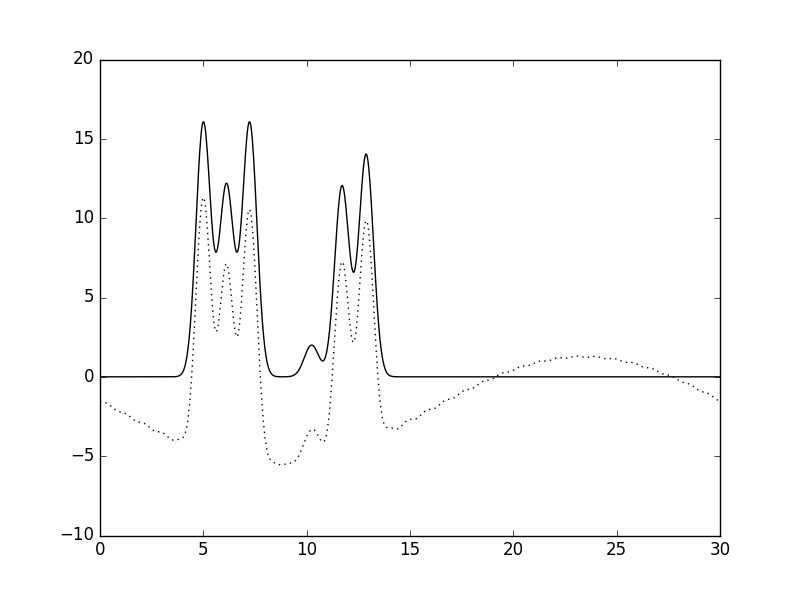 |
Рис. 12 Восстановление функции ЭП по неполному набору гармоник без первых гармоник: без первой 1-32 (слева), без первых двух 2-32 (справа). |
|
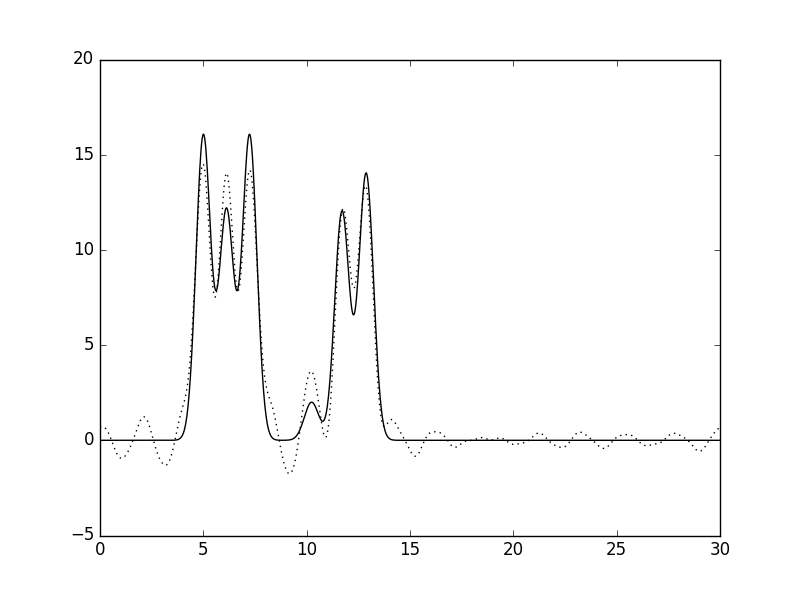
2). На рисунке 13 показаны результаты восстановления функции ЭП по неполному набору гармоник, полученному из полного путём удаления нескольких гармоник из "середины" списка. Видно, что такая модификация уже сильнее влияет на общий вид результата восстановления, чем удаление первых гармоник. Вероятно, если говорить грубо, то именно центральные гармоники несут наибольшую долю информации о функции, в то время как первые задают некие более общие базовые параметры. На рисунке 13 (справа) видно, что крупные атомы восстановлены нормально, а вот водород, например, мало отличим от шума.
 |
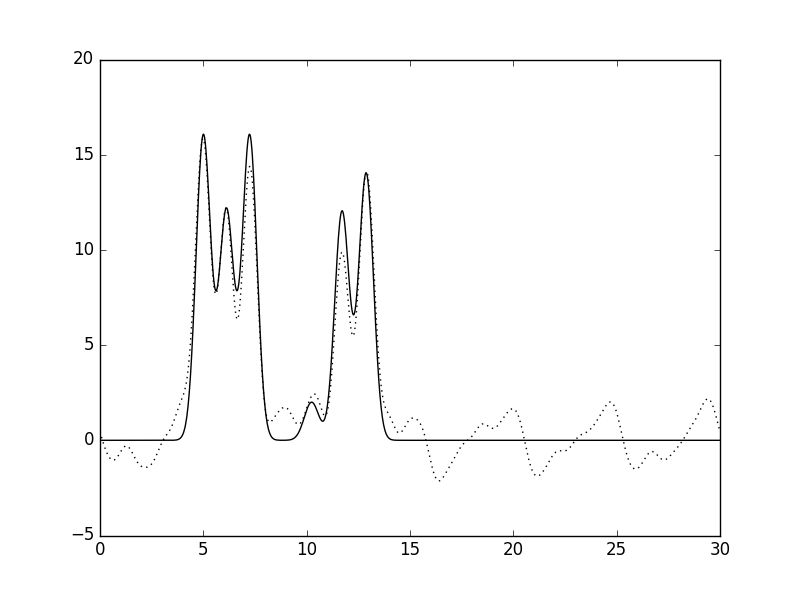 |
Рис. 13 Восстановление функции ЭП по неполному набору гармоник без ряда гармоник из середины списка: без гармоник 14-16 (слева) и без гармоник 6,13,19 (справа). |
|
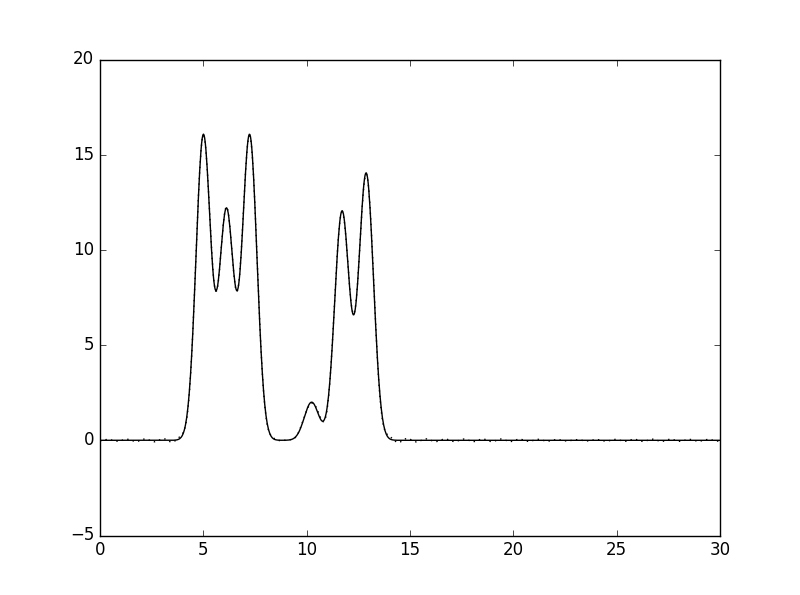
3). На рисунке 14 показаны результаты восстановления функции ЭП при добавлении к списку гармоник дополнительных гармоник с номерами +5 и +10 от номера n0=32. Видно, что добавление дополнительных гармоник в конец списка никак не влияет на результат восстановления функции ЭП. Из этого следует, что гармоники в конце списка имеют скорее уточняющий характер, нежели несут ключевую информацию о характере функции ЭП.
 |
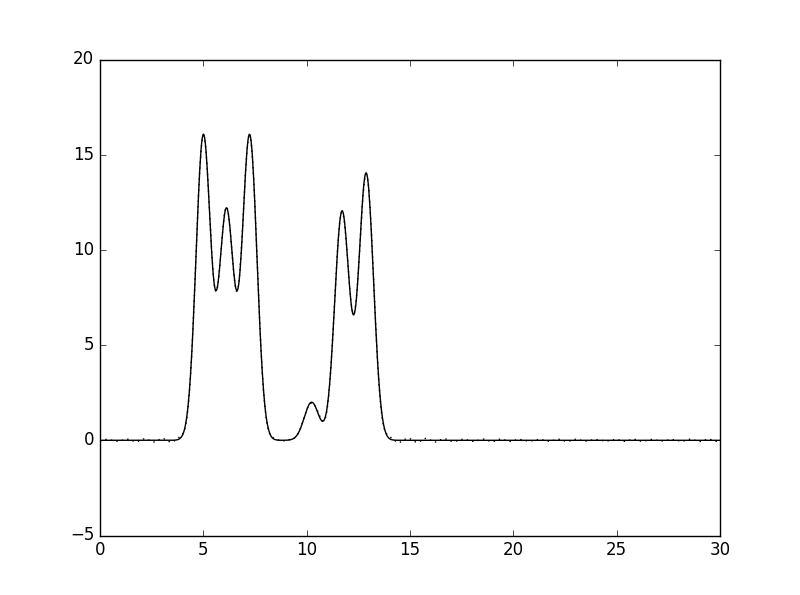 |
Рис. 14 Восстановление функции ЭП по набору гармоник с добавленными +5 (слева) и +10 (справа) элементами. |
|
4). Теперь построим некую ситуацию, наиболее близкую к реальной. Возьмём следующие параметры: n=30, удалим гармоники 6 и 18 как те, которые нам не удалось измерить, добавим 4% шума по обеим характеристикам (амплитуды и фазы). Видно, что тяжёлые атомы неплохо реконструируются, в то время как атом водорода плохо отличается от введённого нами шума и возмущений, которые стали результатом удаления пары гармоник из центра списка.
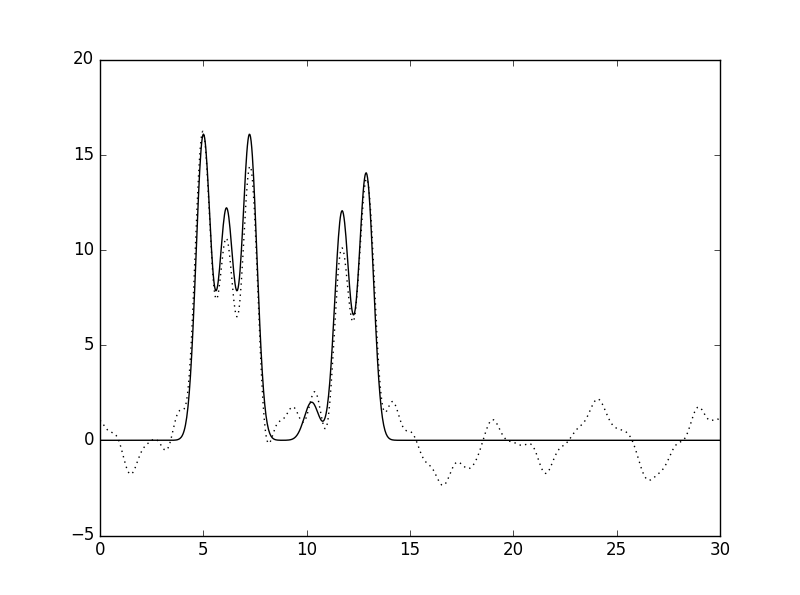 |
Рис. 14 Восстановление функции ЭП для параметров, наиболее приближённо описывающих реальную ситуацию рентгеновского эксперимента (см. в тексте). |
Как определить разрешение набора гармоник?
Если наш набор гармоник полный, то по определению разрешение такого набора есть длина волны гармоники с наибольшим номером. Мы и ранее так определяли разрешение (см. определение числа n0). Что же делать с неполным набором гармоник? Конкретного метода нет, но понятно, что надо каким-то образом учесть ухудшение разрешения при неполноте набора. Вероятно, необходимо сделать некоторую поправку (ввести коэффициент поправки), например, такой d=d0*α, где d0 - разрешение полного набора гармоник, а α есть 1/n, где n - полнота набора гармоник в долях от полного.Краткие результаты и выводы
В таблице 1 приведены характеристики всех восстановлений функции ЭП по набору гармоник. При анализе всех результатов моделирования можно отметить, что наибольшее влияние имеют шум в фазах гармоник и неполнота набора, особенно, когда не хватает гармоник из "середины" списка. 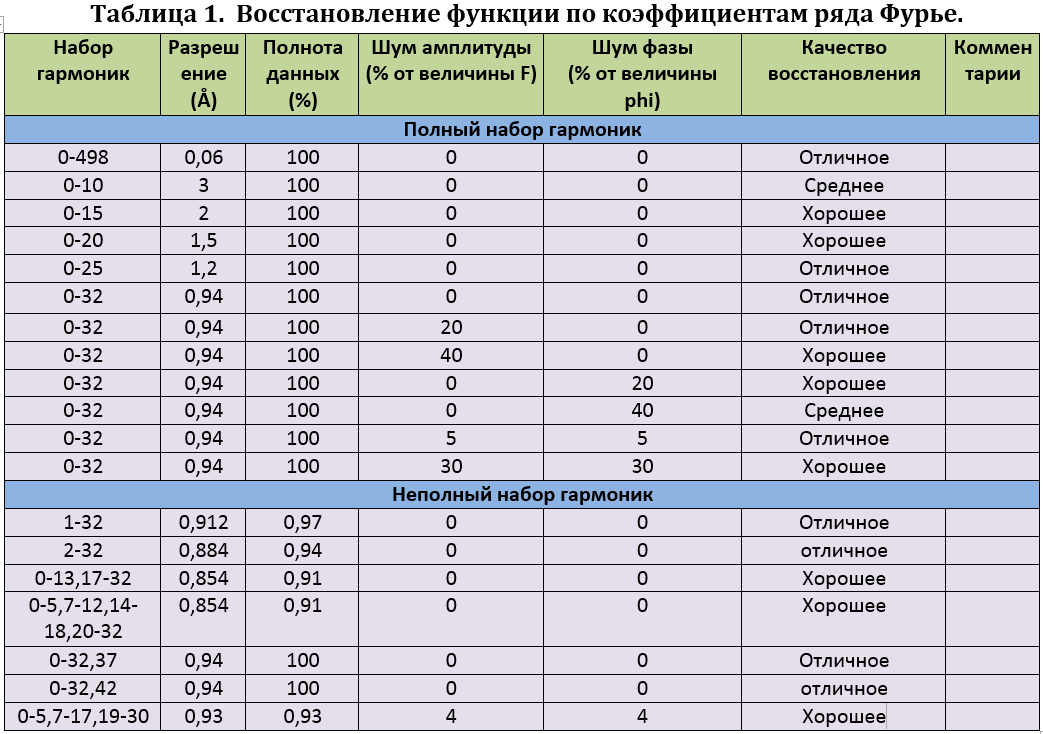 |
Дата последнего обновления: 27.12.2015
© Dmitry Travin, 2015