Моделирование и реконструкция эволюции гена
Создание "истинной" модели и подготовка к реконструкции
Модель эволюции белка представлена скобочной формулой:
((((А:50,B:50):15,C:90):10,D:90):5,(E:60,F:60):40);
Основываясь на ней, было построено следующее дерево:
Это укорененное неультраметрическое (расстояния от листьев до корня не одинаковы)
бинарное дерево. Корню соответствует ген белка BTUB_ECOLI. Ниже представлена таблица
разбиений этого дерева внутренними ветвями (ветви, отделяющие по одному листу, не показаны)
Далее было предложено сгенерировать виртуальные мутантные последовательности соответствующие листьям этого дерева.
Для этого использовалась программа msbar. Скрипт, создающий необходимые последовательности, представлен ниже:
msbar btub_ecoli_gene.fasta EF.fasta -point 4 -count 738 -auto
Z = (N/100)*z;
где N = 1845 - длина гена,
z - количество замен на 100 нуклеотидов (из скобочной формулы).
Необходимые нам последовательности были помещены в один FASTA-файл.
fdnaml mutants.fasta -ttratio 1 -auto
Построенное это программой дерево выглядит следующим образом:
Данные в таблице упорядочены по убыванию "истинных" расстояний. Далее, для оценки точности метода на основе данной, была составлена таблица отклонений (абсолютное значение разности между расстоянием, посчитанным методом, и "истинным"). Отклонения для каждого алгоритма суммировались по всем парам узлов. Полученные результаты:
Из этих данных следует, что наиболее близкую к "истинной" модель реконструировал алгоритм Neighbor-joining. Однако, взглянув на исходное дерево, можно заметить, что листья имеют различное количество промежуточных "предков" на пути от нашего гена. Это значит, что при генерации программой msbar последовательностей, соответствующих этим листьям, происходило перемешивание наборов заменяемых остатков. Следовательно, чем больше промежуточных последовательностей (итераций) создавалось на пути к листу, тем выше вероятность кратной замены в одной и той же позиции, что существенно снижает "видимое" расстояние между последовательностями. Отсюда следует очевидная корреляция между количеством итераций для каждого листа и разностью между рассчитываемым конкретным методом расстоянием и его "реальным" значением. Причем очевидно, что в данном случае (для расстояний от последовательности-мутанта до исходного предка) "видимое" расстояние должно быть не больше, чем "реальное".
По полученным данным был построен график зависимости этого коэффициента от количества итераций для каждого представленного метода:
A B C D E F
- - * * * *
- - - * * *
- - - - * *
msbar EF.fasta E.fasta -point 4 -count 1107 -auto
msbar EF.fasta F.fasta -point 4 -count 1107 -auto
msbar btub_ecoli_gene.fasta ABCD.fasta -point 4 -count 92 -auto
msbar ABCD.fasta D.fasta -point 4 -count 1660 -auto
msbar ABCD.fasta ABC.fasta -point 4 -count 184 -auto
msbar ABC.fasta C.fasta -point 4 -count 1660 -auto
msbar ABC.fasta AB.fasta -point 4 -count 277 -auto
msbar AB.fasta A.fasta -point 4 -count 922 -auto
msbar AB.fasta B.fasta -point 4 -count 922 -auto
Количество замен, которые было необходимо сделать в каждом шаге, вычислялись по следующей тривиальной формуле:
Реконструкция эволюции гена различными методами
Алгоритм макcимального правдоподобия
Данный алгоритм осуществляется программой fdnaml. Строка запроса выглядит следующим образом:
+------------B
|
| +---------------F
| +----------4
| +--3 +-------------E
| | |
1--2 +--------------------D
| |
| +---------------------C
|
+-----------A
Это неукорененное дерево, то есть его следует рассматривать как множество всевозможных укоренений.Алгоритм Neighbor-joining
Данный алгоритм работает с матрицами попарных расстояний, следовательно сначала необходимо создать такую матрицу для наших
последовательностей. Этим занимается программа fdnadist. Полученная матрица подается на вход программе fneighbor, которая
по умолчанию реализует данный алгоритм. Ниже показано дерево, построенное методом Neighbor-joining:
+------------B
!
! +----------------------C
3-4
! ! +--------------------D
! +---2
! ! +-------------E
! +-----------1
! +---------------F
!
+------------A
Это также неукорененное дерево.Алгоритм UPGMA
Этот алгоритм осуществляется той же программой fneighbor, но с указанием данного метода. На вход также подается матрица попарных расстояний.
Построеное UPGMA дерево выглядит так:
+------------------------A
+-----------1
+---3 +------------------------B
! !
+-----4 +------------------------------------C
! !
--5 +----------------------------------------D
!
! +----------------------------E
+-----------------2
+----------------------------F
Это дерево имеет корень, то есть однозначно задает эволюционную модель.Сравнение методов реконструкции эволюции гена
Собственно сравнивать идентичные результаты смысла нет. Каждый алгоритм абсолютно верно построил филогенетическое дерево, совпадающее по топологии
с исходным. Можно отметить лишь алгоритм UPGMA, который построил укорененное дерево (причем укоренил правильно).
Для детального сравнения представленных методов были взяты данные об эволюционных расстояниях между парами соседних узлов (соединенных одной внутренней ветвью), которые содержатся в отчете каждой программы. По ним была составлена сводная таблица:
Пара узлов
Максимальное
правдоподобие Neighbor-joining
UPGMA
"Истинные"
значения
ABCD—D
0,6788
0,68783
0,68478
0,9
ABC—C
0,73257
0,75558
0,62174
0,9
EF—F
0,51178
0,51618
0,48678
0,6
EF—E
0,44428
0,45737
0,48678
0,6
AB—A
0,39793
0,41623
0,41297
0,5
AB—B
0,41681
0,40971
0,41297
0,5
ABCD—EF
0,34889
0,39361
0,39208
0,45
AB—ABC
0,09349
0,07493
0,20877
0,15
ABC—ABCD
0,07979
0,1046
0,06304
0,1
Расстояние между узлами ABCD и EF для метода UPGMA рассчитывалось как сумма расстояний от этих узлов до корня.
Однако помимо количества итераций на значение "видимого" расстояния также влияет и количество замен на каждом шаге итерации: чем больше замен происходит при переходе от одной последовательности к другой, тем также выше вероятность кратных замен одной позиции.
На основе всего вышесказанного введем следующий разностный коэффициент kl, для l-го листа:
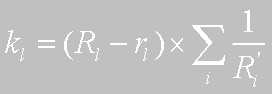
где Rl — "истинное" расстояние между листом l и корнем дерева;
rl — "видимое" методом расстояние между листом l и корнем дерева;
Ri' — "истинное" расстояние на каждом шаге итерации.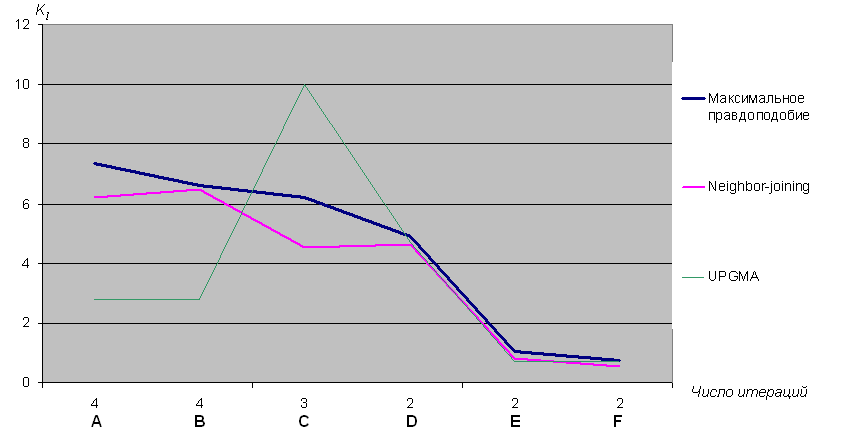
На данном графике четко прослеживается убывание значения kl, при убывании числа итераций для метода максимальной правдоподобности. Чуть хуже ведет себя график алгоритма Neighbor-joining. И совсем хаотично распределен kl для случая UPGMA (может быть потому что он строит ультраметрическое дерево?!!). На самом деле вовсе не обязательно условие монотонности данной функции, очевидно, например, что её значения для пар A, B и E, F в идеале должны быть равны, а в общем случае могут быть различны. В нашем случае, по приятной случайности, именно алфавитный порядок обеспечивает монотонность, но никакого глубоко смысла это не несет.
P.S.: такой метод сравнения весьма грубый и вряд ли будет работать в реальных моделях, но в данном случае мы наблюдаем за виртуальными событиями, в рамках которых он работает.
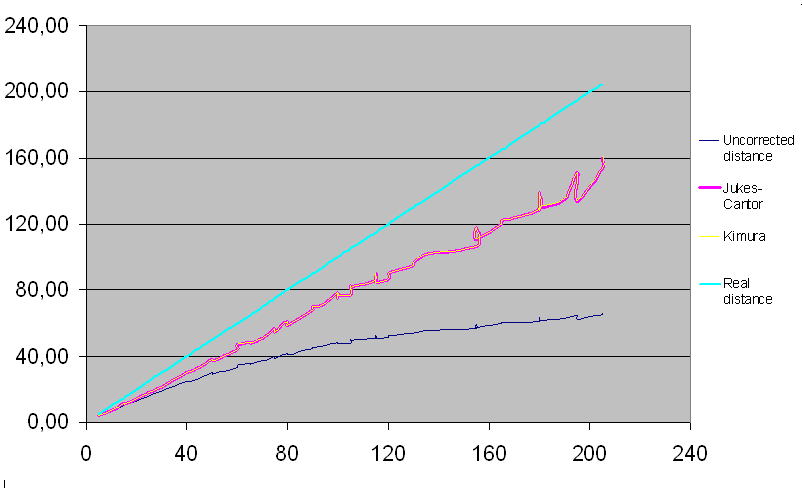
Было предложено сравнить 3 метода вычисления матриц попарных расстояний (МПР). Эталоном сравнения является матрица "истинных" попарных расстояний.
При этом для сравнения использовались все возможные расстояния на дерево (включая между узлами).
Можно сделать вывод, что эти методы хорошо использовать при очень малых расстояниях
между последовательностями (слева все графики практически сходятся в одной точке), тогда как
для далеких последовательностей едва ли возможно создать строгий метод рассчета расстояний.
Попробуем проанализировать поведение kl, взяв за образец метод максимальной правдоподобности и обращаясь к "истинному" дереву. Случаи четырех итераций соответствует мутантам A и B. Это последовательности с наименьшим расстоянием до предка, и, если бы не промежуточные узлы (итерации), их реконструкция была бы очень близка к "истинной" модели. Мутанту С предшествуют три итерации и его kl несколько меньше, но тот факт, что это самая далекая последовательность от предка, не позволяет достаточно точно реконструировать его судьбу. Наконец, три оставшихся мутанта претерпевают всего две итерации. Причем резкое снижение kl наблюдается лишь у E и F. Дело в том, что у этих белков расстояния на обоих шагах итерации небольшие, тогда как вторая итерация мутанта D предусматривает замену 90% нуклеотидов, и, даже не смотря на то, что первая итерация совсем маленькая, этого достаточно чтобы существенно повысить значение его kl.
Все данные, использовавшиеся в этой работе можно найти в файле Excel.
Сравнение разных способов оценки эволюционных расстояний между двумя генами
МПР вычисляются при помощи программы distmat. Выбор метода осуществляется изменением параметров.
Все данные были занесены в Excel-файл. На листе Alldata представлены 4 матрицы попарных расстояний. Лист Comparison содержит сводную таблицу и график зависимости оценок расстояния от величины "истинного" расстояния.
Сводная таблица напоминает предыдущую задачу, но в данном случае мы не имеем дело с деревом как таковым, поэтому можно обойтись простым сравнительным анализом. На полученном графике два метода (Jukes-Cantor и Kimura) практически идентично определили величину попарных расстояний, которые, как и следовало ожидать, меньше истинных.
Причем, чем больше количество замен, тем сильней отличаются предсказания расстояний от истинных значений.
Результаты их практически идентичны, поскольку частоты транзиции и трансверсии в нашей модели равны. Именно эту модель поддерживает метод Джукса-Кантора,
тогда как Кимура учитывает, что эти частоты могут отличаться, поэтому если бы в нашей модели было так, предсказание по Кимура оказалось бы лучше, чем по Джуксу-Кантору.
Метод попарных различий показал худшие результаты, существенно занизив реальные расстояния.
Более того, его график кажется стремится к некой горизонтальной ассимптоте (в отличии от
других двух методов, графики которых более менее линейны).