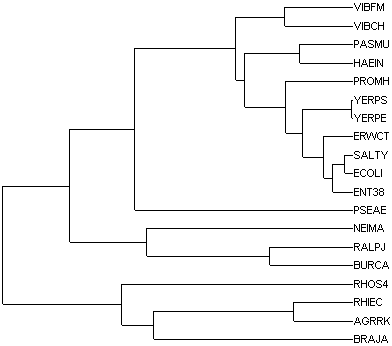
построим филогенетическое дерево выбранных организмов:
Выбраны из заданного списка бактерий 8 представителей, приведенных в таблице ниже:
| Название | Мнемоника |
| Agrobacterium tumifaciens | AGRRK |
| Rhodobacter sphaeroides | RHOS4 |
| Neisseria meningitidis | NEIMA |
| Pseudomonas aeruginosa | PSEAE |
| Erwinia carotovora | ERWCT |
| Escherichia coli | ECOLI |
| Salmonella typhimurium | SALTY |
| Ralstonia pickettii | RALPJ |
Руководствуясь приведённым филогенетическим деревом:

построим филогенетическое дерево выбранных организмов:
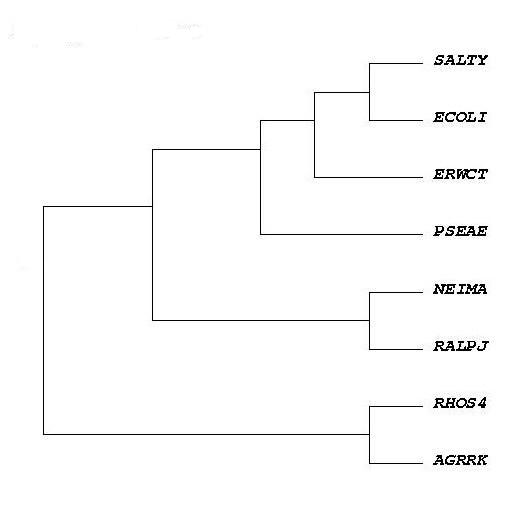
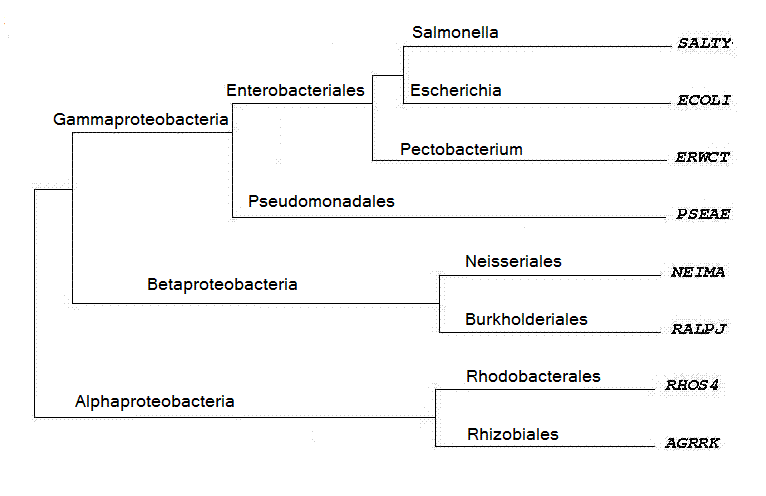
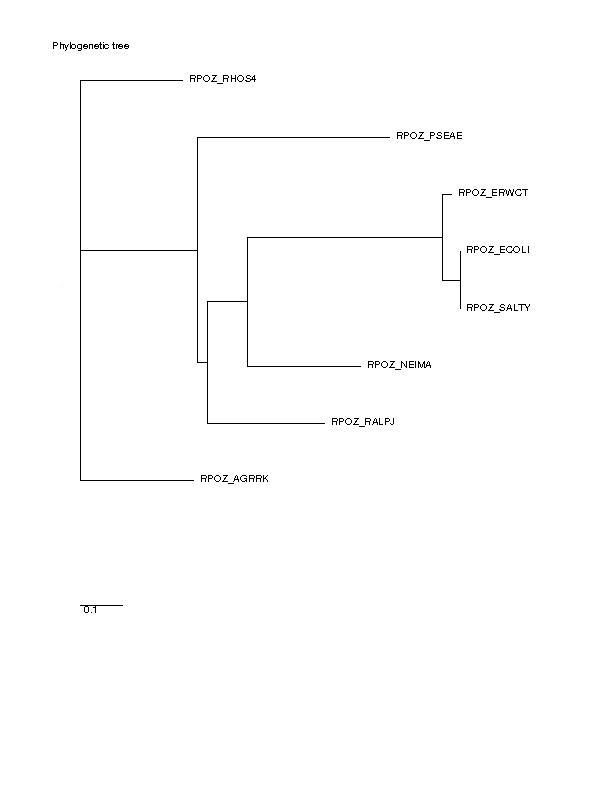
рис.1
Дерево содержит 5 нетривиальных ветвей:
1){SALTY, ECOLI} против {AGRRK, RHOS4, NEIMA, PSEAE, ERWCT, RALPJ}
2){SALTY, ECOLI, ERWCT} против {AGRRK, RHOS4, NEIMA, PSEAE, RALPJ}
3){SALTY, ECOLI, ERWCT, PSEAE} против {AGRRK, RHOS4, NEIMA, RALPJ}
4){SALTY, ECOLI, ERWCT, PSEAE, NEIMA, RALPJ} против {AGRRK, RHOS4}
5){SALTY, ECOLI, ERWCT, PSEAE, AGRRK, RHOS4} против {NEIMA, RALPJ}
Подпишем ветви, выделяющие таксоны, на рисунке 1.
Для реконструирования филогенетического дерева выбрана функция "Омега-субъединица ДНК-зависимой РНК-полимеразы", мнемоника которой RPOZ.
Получили последовательности белков из Swiss-Prot с данной функцией из отобранных раннее бактерий в файл proteins.fasta.
С помощью программы muscle построили множественное выравнивание последовательностей этих белков в файле.
Обсуждение результатов этого выравнивания здесь.
Программой fprotpars провели реконструкцию дерева, изображенного на рис.1
На вход программе подается файл с выравненными последовательностями белков.
В результате получено одно дерево(proteins_aligned.fprotpars ).
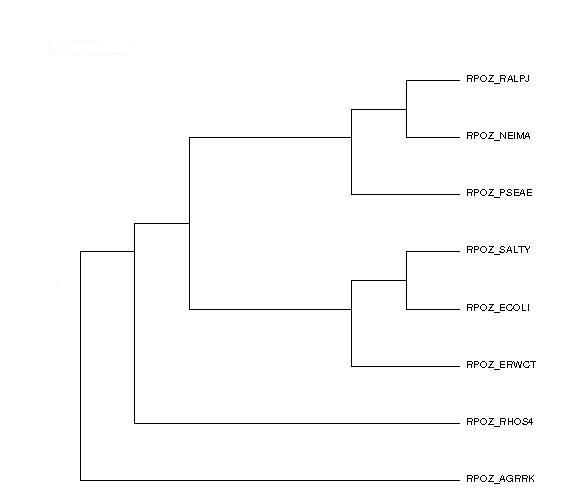
Есть несколько отличий между двумя полученными разными способами филогенетическими деревьями:
С помощью данной программмы можно оценить эволюционные расстояния между последовательностями.
Результат запуска fprotdist для полученных ранее последовательностей:
Computing distances:
RPOZ_AGRRK
RPOZ_RHOS4 .
RPOZ_ERWCT ..
RPOZ_ECOLI ...
RPOZ_SALTY ....
RPOZ_PSEAE .....
RPOZ_NEIMA ......
RPOZ_RALPJ .......
Матрица расстояний
8
RPOZ_AGRRK 0.000000 0.514907 1.148540 1.153820 1.153820 0.948483 0.993756 0.847439
RPOZ_RHOS4 0.514907 0.000000 1.129533 1.117747 1.117747 1.040080 0.829497 0.857569
RPOZ_ERWCT 1.148540 1.129533 0.000000 0.065701 0.065701 0.968992 0.751120 0.964070
RPOZ_ECOLI 1.153820 1.117747 0.065701 0.000000 0.000010 1.007247 0.779722 0.972634
RPOZ_SALTY 1.153820 1.117747 0.065701 0.000010 0.000000 1.007247 0.779722 0.972634
RPOZ_PSEAE 0.948483 1.040080 0.968992 1.007247 1.007247 0.000000 0.957697 0.748470
RPOZ_NEIMA 0.993756 0.829497 0.751120 0.779722 0.779722 0.957697 0.000000 0.547241
RPOZ_RALPJ 0.847439 0.857569 0.964070 0.972634 0.972634 0.748470 0.547241 0.000000
1)d(RPOZ_AGRRK, RPOZ_RHOS4) = 0.514907Отклонение в данном случае: 1.148540-1.129533=0.019007
d(RPOZ_AGRRK, RPOZ_ERWCT) = 1.148540
d(RPOZ_RHOS4, RPOZ_ERWCT) = 1.129533
2)d(RPOZ_ECOLI, RPOZ_SALTY) = 0.000010Отклонение равно 0, таким образом расстояние ультраметрично.
d(RPOZ_ECOLI, RPOZ_PSEAE) = 1.007247
d(RPOZ_SALTY, RPOZ_PSEAE) = 1.007247
3)d(RPOZ_PSEAE, RPOZ_NEIMA) = 0.957697Отклонение равно 0.209227
d(RPOZ_PSEAE, RPOZ_RALPJ) = 0.748470
d(RPOZ_NEIMA, RPOZ_RALPJ) = 0.547241
d(RPOZ_ECOLI, RPOZ_SALTY) = 0.000010 (1)
d(RPOZ_ECOLI, RPOZ_PSEAE) = 1.007247 (2)
d(RPOZ_SALTY, RPOZ_PSEAE) = 1.007247 (3)
d(RPOZ_ECOLI, RPOZ_ERWCT) = 0.065701 (4)
d(RPOZ_ERWCT, RPOZ_SALTY) = 0.065701 (5)
d(RPOZ_ERWCT, RPOZ_PSEAE) = 0.968992 (6)
(1)+(6)=0.969092
(3)+(4)=(2)+(5)=1.072948
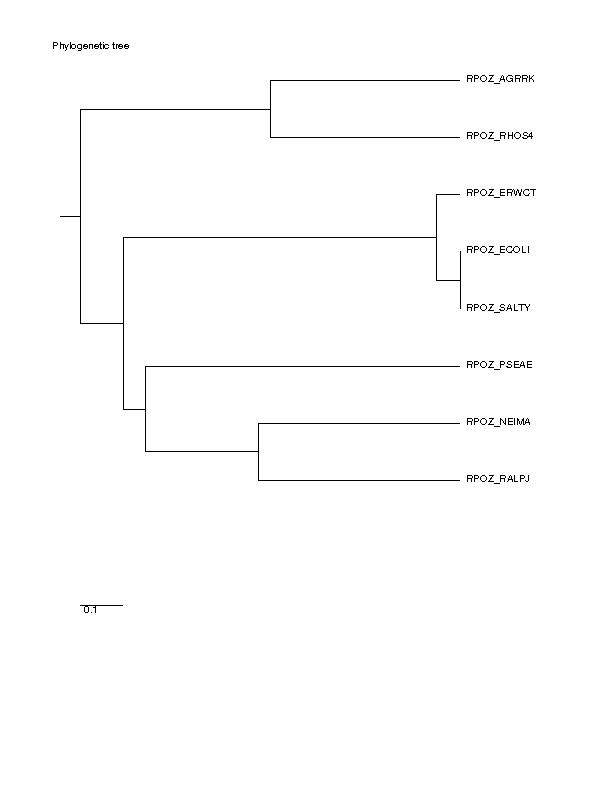
Скобочные формулы
((((((SALTY, ECOLI), ERWCT), NEIMA), RALPJ), PSEAE), (AGRRK, RHOS4)) - Neighbor-Joining
((((SALTY, ECOLI), ERWCT), (PSEAE, (NEIMA, RALPJ))), (AGRRK, RHOS4)) - UPGMA
fneighbor и fprotpars
Общее для деревьев, полученных программами fneighbor и fprotpars - клада {SALTY, ECOLI, ERWCT}
Сравнивая все деревья с правильным на рис. 1, получаем, что топология каждого из деревьев различна, но можно заметить, что клада {SALTY, ECOLI, ERWCT} является общей для всех полученных деревьев.
Таким образом, можно утверждать, что самыми последними отделились Enterobacteriales, а Alphaproteobacteria - первыми из представленных организмов.