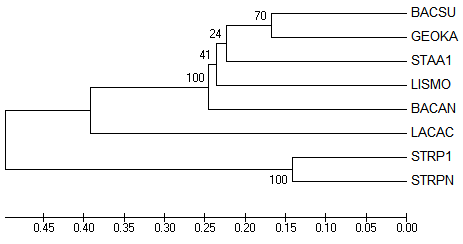
Укоренение в среднюю точку - метод укоренения дерева, при котором выбирается самый длинный путь между двумя таксонами, производится укоренение в середину этого пути.
Укоренение производилось на неукорененных деревьях, построенных методом Neighbor Joining, с помощью программы retree пакета PHYLIP.
Важно отметить, что без использования переукоренения, MEGA сама укореняет открываемое newick-дерево после NJ в случайную точку,
это можно увидеть на примере предыдущих заданий (занятие 2, задание 4).
retree пакета PHYLIP имеет необычный интерфейс, по умолчанию на вход принимает файл intree, выдает файл outree.
Доступные способы изменения дерева:
R - переместить поддерево (использовалось мною для переукроенения при работе с
занятием 2, заданием 4)
O - выбрать аутгруппу дерева
M - укоренить в среднюю точку
T - перенести ближайшие ветви в узел (вершину) (? на деле почему-то работает так же, как и F)
F - вращать поддерево вокруг узла
D - удалить или восстановить ветви
B - поменять или добавить длины ветвей
N - поменять или добавить имена
Другие доступные действия:
. - обновить дерево
= - сменить режим просмотра длин ветвей
U - отменить последние изменения дерева
W - запись файл (есть возможность записать укорененное или неукорененное дерево в newick-формате)
+ - прочитать следующее дерево из файла
C - показать только одно поддерево (кладу)
? - помощь
Q,X - выход из программы
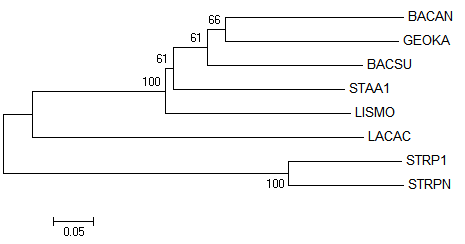
Итак, укорененные в среднюю точку деревья после NJ % Identity и NJ BLOSUM62, соответственно, вид MEGA и retree:
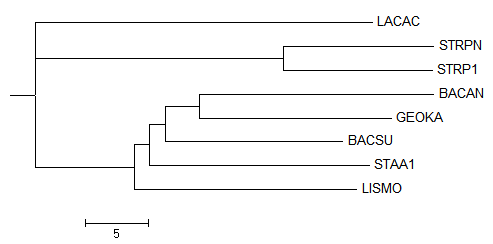
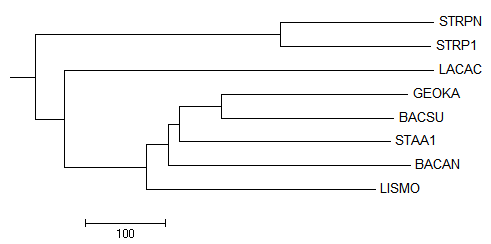
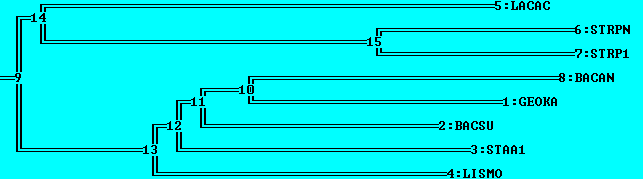
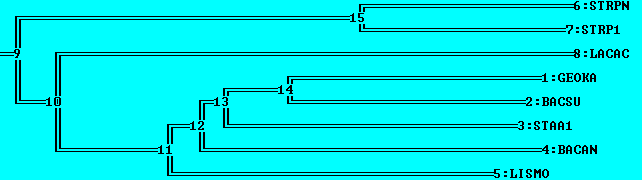
Укоренение после NJ % Identity можно считать правильным, произошло в ветвь, отделяющую всех Lactobacillales от всех Bacillales.
Укоренение после NJ BLOSUM62 неправильное, произошло во внутреннюю ветвь поддерева Lactobacillales.
(Напоминение таксономии здесь: занятие 2, задание 1)
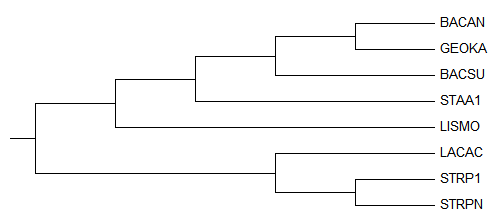
Напоминаю исходное, верное дерево:
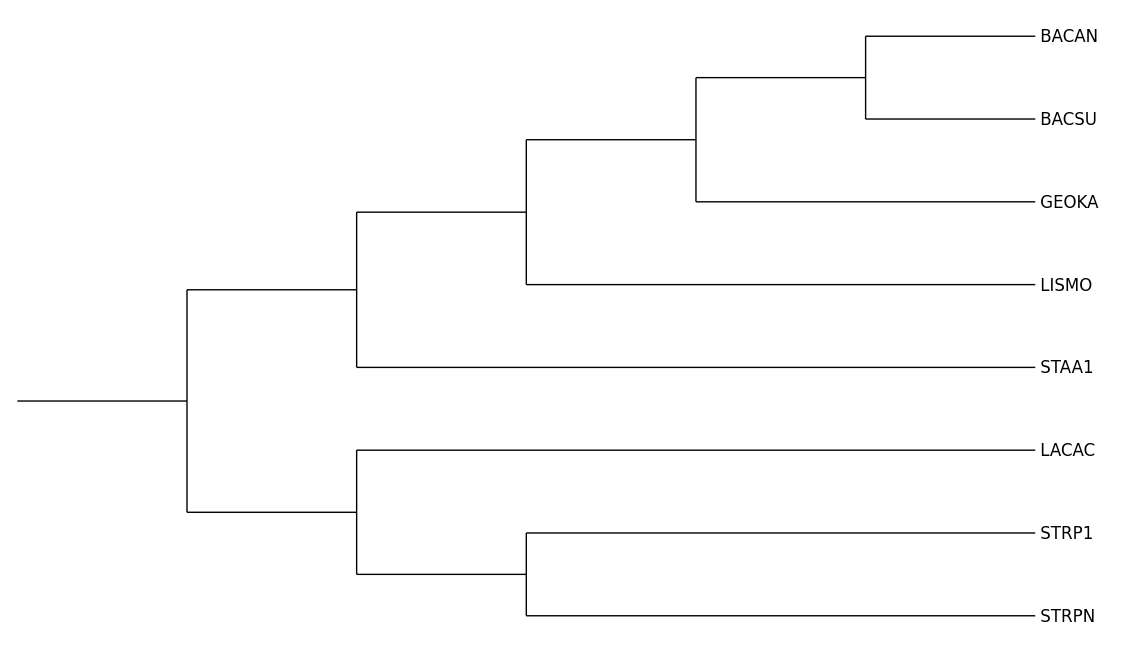
Внешняя группа, или аутгруппа (англ. outgroup) - это поддерево, отделенное от поддерева исследуемых организмов, используемое для поиска ветви для укоренения.
Метод поиска точки укоренения с помощью аутгруппы состоит в следующем:
1. К выборке исследуемых организмов добавляем ещё один или несколько заведомо далеких по таксономии видов - аутгруппу;
2. Стороим совместное выравнивание их исследуемых последовательностей;
3. Стороим по нему дерево (символьно-ориентированным или любым другим методом);
4. Укореняем дерево в ветвь, разделяющую аутгруппу и группу исследуемых организмов;
5. Удаляем аутгруппу.
Метод аутгруппы чаще всего применяется и необходим после работы программ, восстанавливающх неметричные деревья (то есть, только их топологию без длин ветвей).
Очевидно, что применить к полученным таким образом деревьям укоренение, использующее длины ветвей тем или иным способом (как root at midpoint), невозможно.
Maximum Parsimony, MP, максимальная экономия - символьно-ориентированный метод, восстанавливающий только топологию без длин ветвей. На его результирующем дереве и буду изучать
метод аутгруппы.
В текущем задании я добавила в fasta-файл с последовательностями белка HSLO
отобранных в предыдущих заданиях бактерий-фирмикут (Firmicutes)
последовательность HSLO дальней родственницы
из Proteobacteria, известной Escherichia coli.
Далее перевыровняла последовательности, запустила по ним
построение дерева методом MP - максимальной экономии. Далее укоренила в ветвь,
разделяющую Firmicutes от ECOLI.
Полученое дерево:
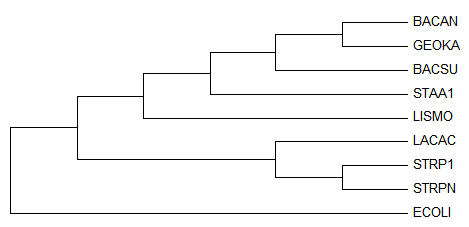
После выбрала для просмотра только поддерево Firmicutes:
Укоренение произошло правильно, но само дерево по-прежнему неверно, комментарии можно увидеть здесь:
занятие 2, задание 5
Бутстреп (англ. bootstrap) - метод проверки достоверности топологии
дерева, основанный
на многократном повторении произвольной выборки с повторениями из
половины столбцов выравнивания и последующего
построения дерева (т.о. на половине исходных данных).
При проведении бутстрепа, каждой ветви возможной присваивается значение -
поддержка - количество случаев присутствия ветви.
Причем значения поддержки можно отразить как на исходном дереве (Original Tree),
так и на консенсусном дереве (Consensus Tree), построенном из непротиворечащих ветвей с максимальной поддержкой.
В текущем задании требовалось методом бутстрепа (100 реплик, сервис MEGA5) найти поддержки ветвей дерева из предыдущих заданий, вывести и сравнить консенсусное.
Алгоритм для построения деревьев: Maximum Parsimony, на выходе - только топология дерева, без длин ветвей.
Полученные деревья: Original tree 1, Original tree 2, Consensus tree, соответственно:
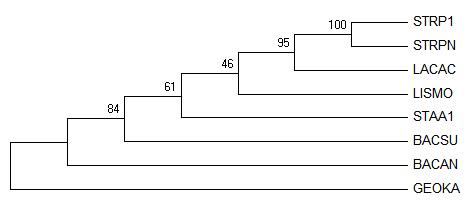
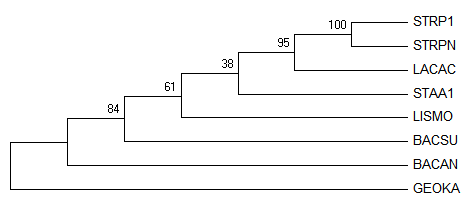

Видно, что поддержка у ветвей
{STRP1, STRPN, LACAC,LISMO}vs{STAA1,BACSU,BACAN,GEOKA} (- 46) и
{STRP1, STRPN, LACAC,STAA1}vs{LISMO,BACSU,BACAN,GEOKA} (- 38)
примерно одинковая, из-за этого программа выдала два возможных дерева.
При этом в консенсусном дереве выбран наиболее поддержанный вариант, при том неправильный.
Правильные ветви с высокой поддержкой:
{STRP1, STRPN}vs{LACAC,STAA1,LISMO,BACSU,BACAN,GEOKA} - 100
{STRP1, STRPN,LACAC}vs{STAA1,LISMO,BACSU,BACAN,GEOKA} - 95
{STRP1, STRPN,LACAC,STAA1,LISMO}vs{BACSU,BACAN,GEOKA} - 61
Неправильные ветви с высокой поддержкой:
{STRP1, STRPN,LACAC,STAA1,LISMO,BACSU}vs{BACAN,GEOKA}
Для сравнения, результаты бутстрепа с использованием UPGMA (дерево ультраметричное, длины ветвей отображены соразмерно) и
NJ (дерево не ультраметрично, длины ветвей соразмерны), cоответственно: