Страница четвертого семестра | Учебный сайт Екатерины Швецовой

Профили. Домены

В рамках данного практикума был исследован предполагаемый домен связывания пептидогликана (PF12229). Этот домен связан с доменом связывания L,D-транспептидазы (PF03734), часто бывает, что он дуплицирован в геноме. Вероятно, этот домен связывает две пептидогликановые цепи и сближает так, чтобы они могли связаться транспептидазным доменом.

Этот домен содержит 16 архитектур, изображение схемы строения некоторых из них можно увидеть на рис. 1. Для дальнейшего рассмотрения были выбраны первая и четвёртая архитектура. Цифрой "2" будем в дальнейшем обозначать архитектуру, содержащую два домена PF12229 и один домен PF03734, а цифрой "1" - содержащую один домен PF12229 и один домен PF03734.

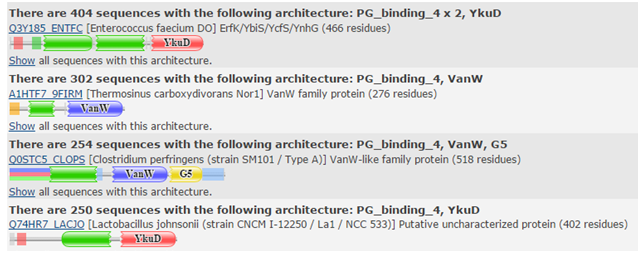
Рис. 1. Схемы строения некоторых архитектур, содержащих домен предполагаемый домен связывания пептидогликана (PF12229).

С сайта PFAM было скачано полное выравнивание всех последовательностей домена открыто в Jalview, покрашено ClustalX By Conservation 0%. Проект выравнивания можно увидеть здесь. Далее была получены таблица, содержащая информацию о доменной структуре каждой последовательности, содержащей данный домен. Это было сделано с помощью скрипта swisspfam-to-xls.py. Команда: "python swisspfam-to-xls.py -z /srv/databases/pfam/swisspfam.gz -m domain_AC.txt -o PF12229.txt". Файл domain_AC.txt должен содержать идентификатор исследуемого домена.

Также были получены сведения о таксономии каждой последовательности. Для этого сначала (из файла PF12229.txt) был получен список идентификаторов последовательностей (скрипт), затем из базы данных uniprot были скачаны соответствующие записи (файл). И затем с помощью другого скрипта (команда: "python uniprot_to_taxonomy.py -i PF12229_uniprot.txt -o PF12229_taxonomy.txt") был получен файл с таксономией.

На основе всех этих данных с помощью скрипта и ресурсов Excel была получена сводная таблица, содержащая список последовательностей с указанием их доменной архитектуры, длины домена PF12229 и таксономии.

В качестве таксона было выбрано царство Bacteria, в качестве подтаксонов типы Firmicutes и Actinobacteria. Затем было выбрано 59 представителей подтаксонов: 26 с архитектурой "2" (выбирались последовательности как первого вхождения домена, так и второго) и 33 с архитектурой "1". Соответствующие им последовательности были вырезаны из общего выравнивания с помощью скрипта, открыты в Jalview. Были удалены плохо выравненные последовательности и небольшие участки с C и N концов. Проект получившегося выравнивания можно сказать здесь. Выравнивание в фаста-формате - alignment_right_names.fasta.

Затем по данному выравниванию в программе MEGA было построено дерево методом Maximum Likelihood. Скобочная формула дерева:

((((((((((((((F_1_B7HAJ8,F_1_G9Q4X8),F_1_B5UM03),(F_1_B3Z442,F_1_B3ZHT6)),F_1_C2MMS6),(F_1_G6EV46,(F_1_E4SYP9,F_1_G6F8W2))),(F_1_B2GDF1,(F_1_C0X002,F_1_D8IIG6))),F_1_G2SR05),F_1_G9ZRW7),F_2_C7RE30),(F_2_A5ZS93,F_1_D4LH16)),((F_2_A5ZNC0,F_2_D6DDN7),(F_2_C2KVQ3,((F_2_A6LRG0,F_2_B1IGW3),(F_2_A7AZ78,F_2_C0BBC4))))),(A_2_C8WPM4,A_1_B6GC68)),A_2_C0W0R7),(((((A_1_B6XV56,A_1_C0BT20),(A_1_B8DUP1,A_1_D1NSC0)),A_1_D3F1C0),A_2_C7MBB0),(A_2_A7BBT1,((F_2_D4N0F9,A_1_G5F5P4),(F_2_B5CTB1,(F_2_D4R893,(F_2_B5CM58,(F_2_C0CGS3,(F_2_A5N5L0,(F_2_A5I3Y3,F_2_A6M0T4))))))))));

Изображение дерева можно увидеть на рис. 2.

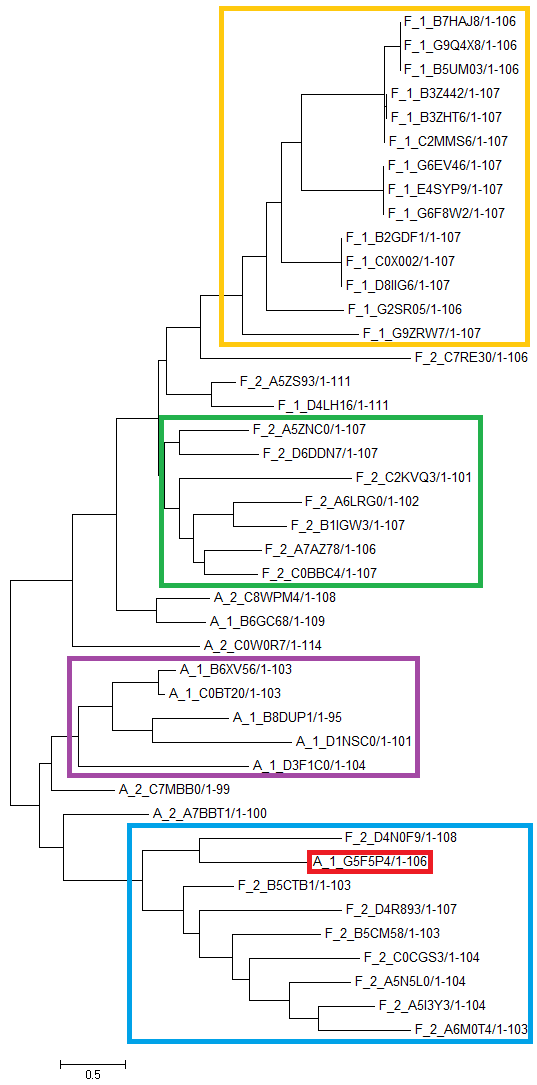
Рис. 2. Филогенетическое дерево домена связывания пептидогликана (PF12229). Построено методом Maximum Likelihood.

На дереве буква "F" в названии последовательности означает, что она принадлежит типу Firmicutes, "А" - Actinobacteria. Цифры "1" и "2" - обозначения доменов (вводились выше). По дереву видно, что последовательности Firmicutes c архитектурой "1" четко выделились в одну кладу (отмечена желтой рамочкой). также можно наблюдать кладу, содержащую почти все последовательности Actinobacteria с архитектурой "1" (фиолетовая рамочка). Последовательности Firmicutes с архитектурой "1" присутствуют в двух больших кладах (зелная и голубая рамочки). красным выделена последовательность, выбивающаяся из клады. Можно предположить следующую эволюцию домена: вероятно, сначала существовала архитектура "2" у Actinobacteria, затем (на разных этапах эволюции) она превносилась в Firmicutes (на дереве отражено два таких примера - две клады с последовательностями F_2_******). Последовательности с архитектурой "1" появились как для Actinobacteria так и для Firmicutes позже, вероятно, в результате потери второй копии домена PF12229.

Наличие выбивающейся последовательности клады, обведенной голубой рамочкой, вероятно связано с тем, что она была плохо (неправильно) выравнена с другими последовательностями.

Для построения профиля в качестве подсемейства последовательностей были выбраны последовательности F_1_****** из клады, выделенной желтой рамочкой (т. к. они отделены от остального дерева). Выравнивание выбранных последовательностей можно посмотреть здесь. По ним с помощью программы hmm2build был построен профиль последовательностей и затем он был откалиброван программой hmm2calibrate. По этому профилю был проведен поиск по всем белкам, включающим домен PF12229 с помощью программы hmm2search. Результат поиска можно увидеть здесь. Всего было найдено 709 последовательностей с E_value от 5,5E-64 до 9,9.

Далее на основе полученных результатов с помощью средств Excel была составлена ROC-кривая, которую можно увидеть на рис. 3. Таблица Excel, в которой производились расчёты - здесь.

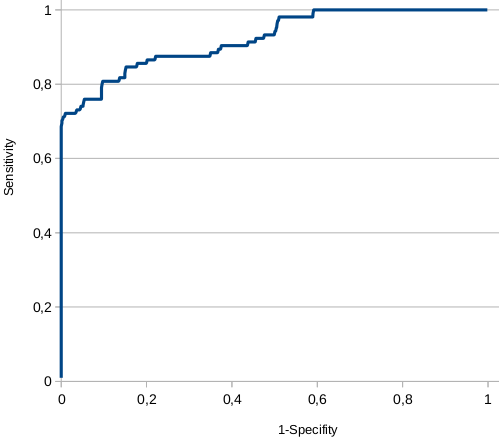
Рис. 3. ROC-кривая. Получена с помощью Excel.

При выбранном пороге E-value 1,5E-45 чувствительность составляет 70,2%, специфичность - 99,8%. Результаты при этом пороге можно найти в таблице 1.

Таблица 1. Результаты поиска по профилю при выбранном пороге E-value 1,5E-45

На самом деле	принадлежит подсемейству	не принадлежит	сумма
Выше порога по профилю	73	1	74
Ниже порога	31	604	635
сумма	104	605	709

Т. к. площадь под ROC-кривой достаточно большая и учитывая то, что при применении выбранного порога E-value почти все последовательности выше порога входят в состав подсемейства, этот профиль можно использовать для его выделения. Однако, т. к. последовательностей, принадлежащих подсемейству и находящихся ниже порога E-value, достаточно много, при таком поиске всё подсемейство выделить трудно.