Главная

Изучение работы методов контроля температуры в GROMACS

• Подготовим файл координат и файл топологии. Создадим индекс файл в котором будет группа из одной молекулы этана на основе 38 gro файлов с молекулами этана.

make_ndx -f box_38.gro -o 1.ndx

• Выбераем остаток номер 1. Появляется новая группа. Теперь создадим gro файл с одной молекулой и зададим ячейку. При запуске editconf выбераем номер, соответствующей группе из одной молекулы.

editconf -f box_38.gro -o et1.gro -n 1.ndx
#зададим ячейку и расположим молекулу по центру ячейку
editconf -f et1.gro -o et.gro -d 2 -c

• Исправим файл топологии et.top из прошлого задания. В разделе [ molecules ] изменим количество молекул этана с 38 на 1.
• Даны 5 файлов с разными параметрами контроля температуры:
  • an.mdp - метод Андерсена для контроля температуры.
  • be.mdp - метод Берендсена для контроля температуры.
  • nh.mdp - метод Нуза-Хувера для контроля температуры.
  • sd.mdp - метод стохастической молекулярной динамики.
  • vr.mdp - метод "Velocity rescale" для контроля температуры.

Напишем скрипт bash для работы с 5ю системами.

• Создаём отдельную папку для каждого метода.

mkdir ${i}

• Построим входные файлы для молекулярно-динамического движка mdrun с помощью grompp:

grompp -f ${i}.mdp -c et.gro -p et.top -o et_${i}.tpr

• У нас получилось 5 tpr файлов. Теперь для каждого из них запустим mdrun.

mdrun -deffnm et_${i} -v -nt 1

Анализ

• Для каждой из 5 систем проведем конвертацию в pdb и просмотрим в PyMol.

trjconv -f ${i}/et_${i}.trr -s ${i}/et_${i}.tpr -o ${i}/et_${i}.pdb

• ролики для PyMOL:

  • et_an.pdb

  • et_be.pdb

  • et_nh.pdb

  • et_sd.pdb

  • et_vr.pdb

• Наблюдения:
  • В методе Андерсена наблюдаются небольшие колебания по длинам связей и валентным углам. Вращение в данном случае отсутствует.
  • В методе Берендсена сперва мы наблюдать различные колебания и вращения.
  • В методе Нуза-Хувера мы наблюдаем небольшие колебания и вращение по связи С-С.
  • В методе стохастической молекулярной динамике молекула очень быстро вращается и перемещается. Сложно уследить что происходит.
  • Метод "Velocity rescale". Можно наблюдать более амплитудные колебания и уменьшенное вращение по связи С-С.

Сравним потенциальную энергию связи и кинетическую энергию для каждой из 5 систем

g_energy -f et_${i}.edr -o et_${i}_en.xvg

• Построим графики изменения энергий. Для этого в баш скрипте добавим строчки скрипта для Gnuplot:

echo -e "set datafile commentschars '#@&'
set term 'png'
set output '${i}/en_${i}.png'
plot '${i}/et_${i}_en.xvg' using 1:2, '${i}/et_${i}_en.xvg' using 1:3" > ${i}/en_${i}.gnu
gnuplot < ${i}/en_${i}.gnu

Рассмотрим распределение длинны связи С-С за время моделирования

• Сначала создадим индекс файл с одной связью.

В текстовом редакторе создим файл b.ndx со следующим содержимым:

[ b ]
1 2

• запустим утилиту по анализу связей g_bond:

g_bond -f et_${i}.trr -s et_${i}.tpr -o bond_${i}.xvg -n b.ndx

Построим графики распределения длинн связей. Для этого в баш скрипте добавим строчки скрипта для Gnuplot:

echo "set datafile commentschars '#@&'
set term 'png'
set output '${i}/bond_${i}.png'
plot '${i}/bond_${i}.xvg' with boxes" > ${i}/bond_${i}.gnu
gnuplot < ${i}/bond_${i}.gnu

Полученные изображения:

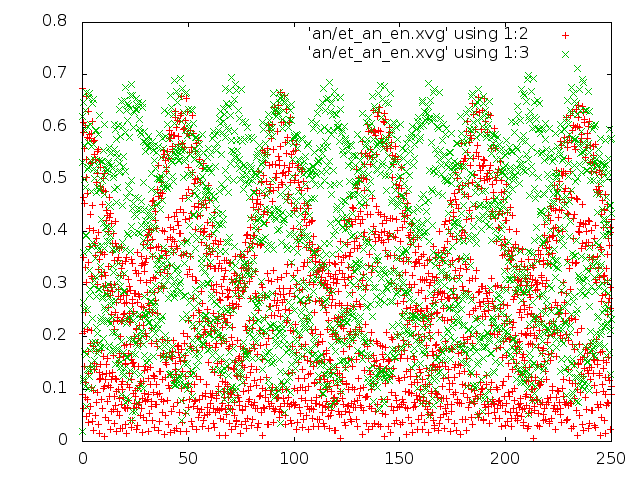
• метод Андерсена.
  • энергия для каждого состояния: красным цветом потенциальная энергия связей, зелёным - кинетическая энергия

    • 

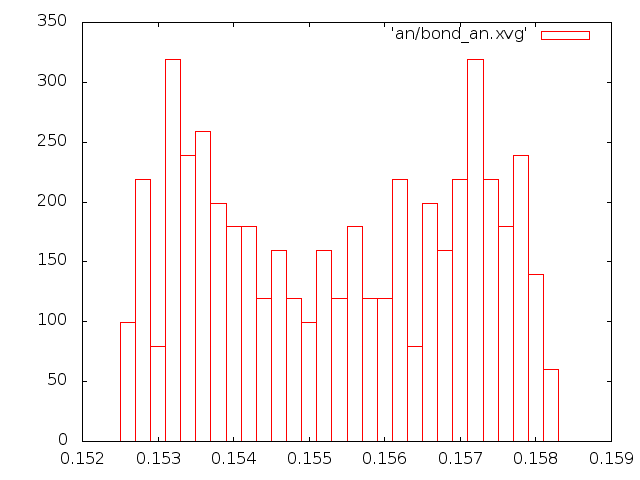
  • распределения длин связей

    • 

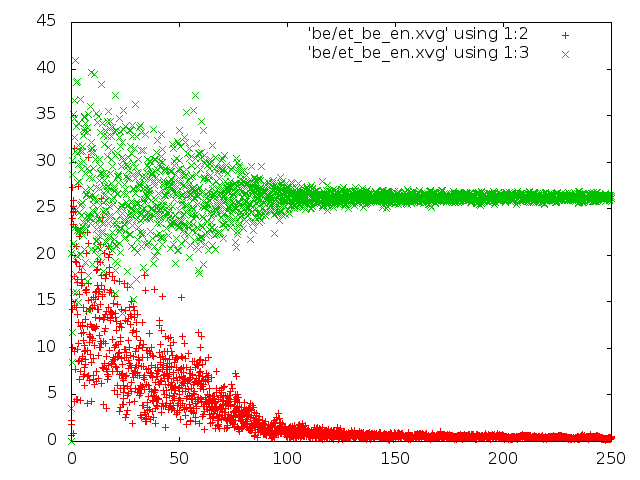
• метод Берендсена.
  • энергия для каждого состояния: красным цветом потенциальная энергия связей, зелёным - кинетическая энергия

    • 

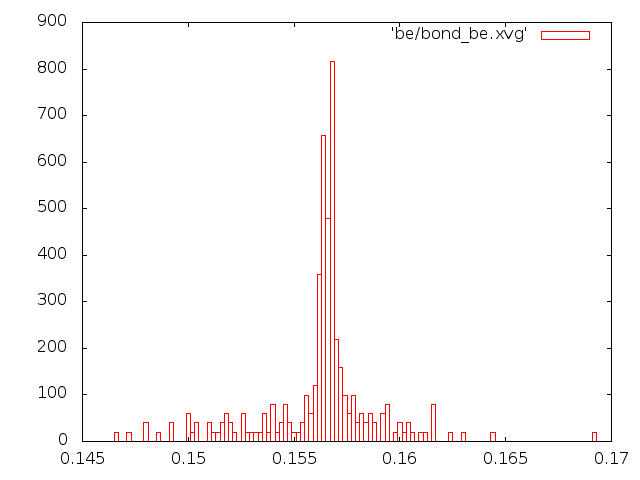
  • распределения длин связей

    • 

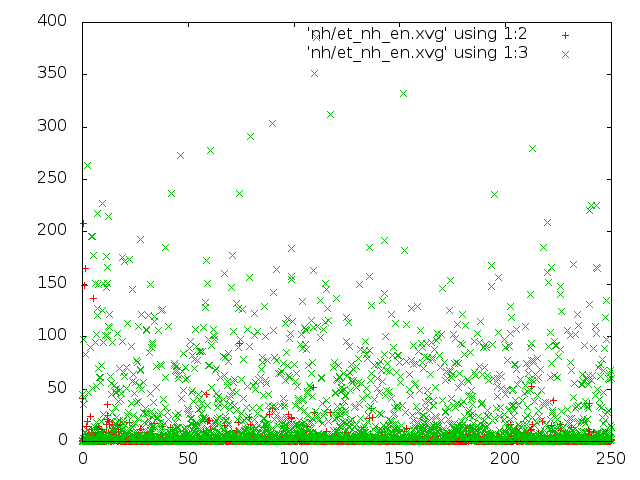
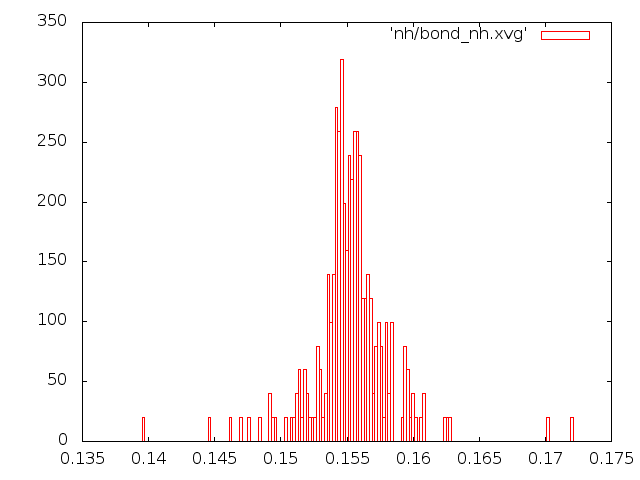
• метод Нуза-Хувера.
  • энергия для каждого состояния: красным цветом потенциальная энергия связей, зелёным - кинетическая энергия

    • 

  • распределения длин связей

    • 

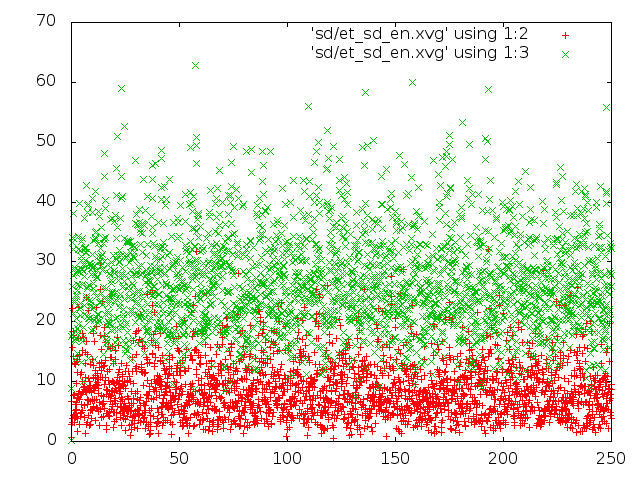
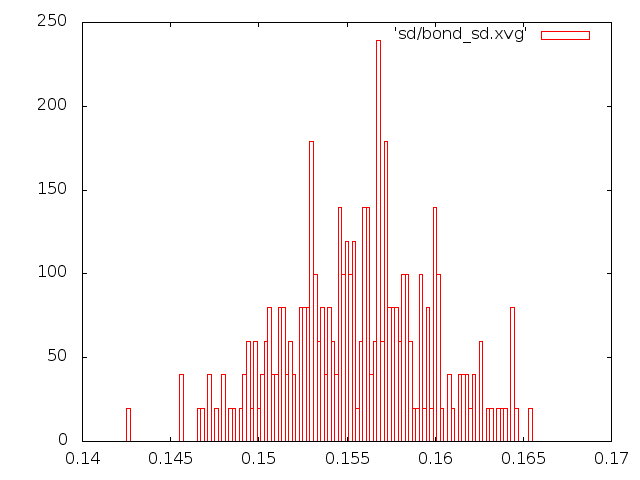
• стохастический метод.
  • энергия для каждого состояния: красным цветом потенциальная энергия связей, зелёным - кинетическая энергия

    • 

  • распределения длин связей

    • 

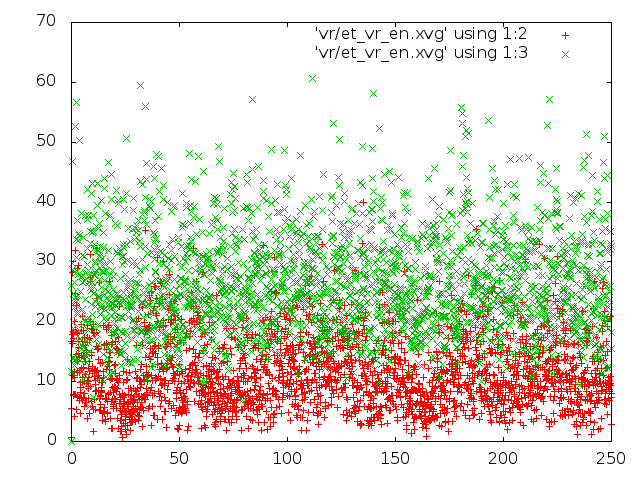
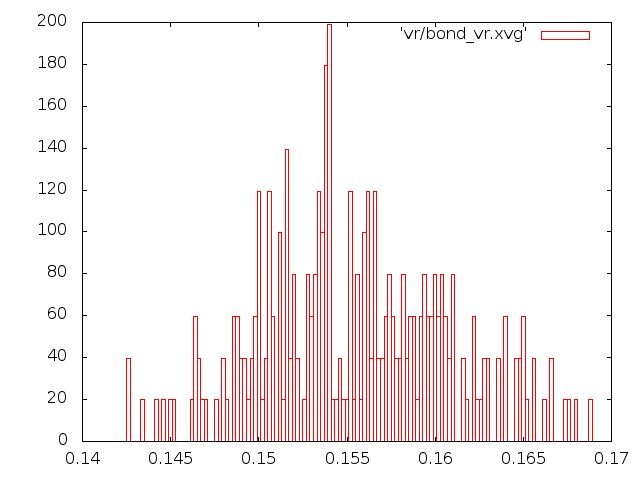
• Метод "Velocity rescale".
  • энергия для каждого состояния: красным цветом потенциальная энергия связей, зелёным - кинетическая энергия

    • 

  • распределения длин связей

    • 

• Исходя из всех наблюдений, можно сказать, что самым реалистичным является метод "Velocity rescale". Метод Андерсена и Берендсена совершенно не соответствует общему виду распределения Больцмана.