Восстановление функции электронной плотности
В данном задании на примере модельной функции электронной плотности рассматриваются зависимости качества восстановления функции ЭП в зависимости от разного количества и порядка гармоник, а также от уровня шума в значениях структурных факторов.
Создание модельной функции ЭП в одномерной элементарной ячейке
Модель представляет собой две молекулы, в первой 3 атома, во второй - 2, расположенные на расстоянии около 5 Å, что соответствует гидрофобному взаимодействию или водородной связи. Внутри молекулы атомы связаны ковалентно и находятся на расстоянии 1 - 1.5 Å.
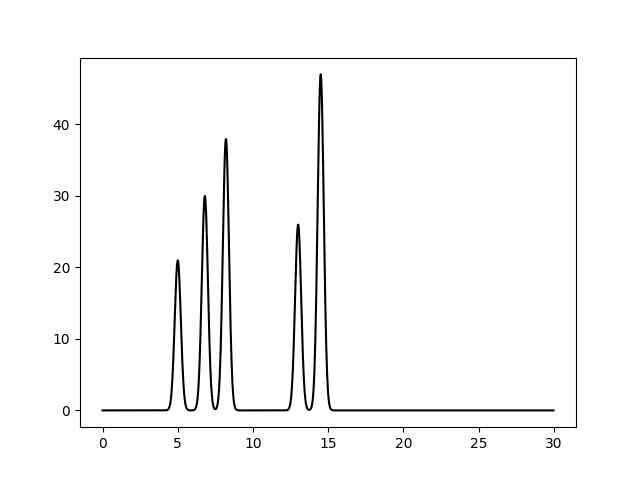
Функция электронной плотности для одномерного случая была смоделирована на участке [0, 30] Å с помощью скрипта compile-func.py, запущенного с параметром -g 21, 3.5, 5 + 30, 3.5, 6.8 + 38, 3.5, 8.2 + 26, 3.5, 13 + 47, 3.5, 14.5. Скрипт моделирует функцию электронной плотности как сумму гауссовских функций, в данном случае 5 функций, каждая из которых описывает электронную плотность вокруг соответствующего атома. Параметры задают характеристики гауссиан: расположение максимумов (5, 6.8, 8.2, 13, 14.5) и высоту пиков (21, 30, 38, 26, 47). Высота пика пропорциональна количеству электронов в атоме, а по положению максимумов можно судить о расстоянии между атомами и молекулами.
На Рис. 1 изображена модельная функция электронной плотности.
Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Смоделированная функция была затем разложена в ряд Фурье с помощью скрипта func2fourier.py. Выдача скрипта содержит 499 гармоник, характеристики которых представлены в виде <номер гармоники> <амплитуда> <фаза>. Сумма полученных гармоник дает исходную функцию.
Выбор n первых гармоник, дающих отличное качество восстановления функции ЭП
Далее было необходимо определить, какое количество первых гармоник достаточно использовать для восстановления функции ЭП с отличным качеством. Для этого сначала определим критерии качества:
- Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"
- Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно
- Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума
- Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")
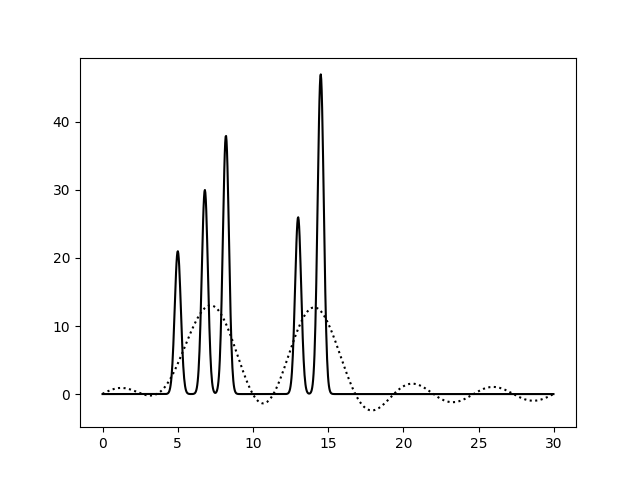
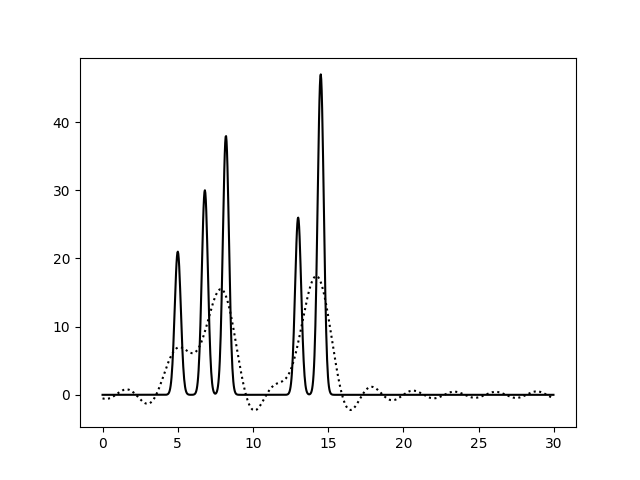
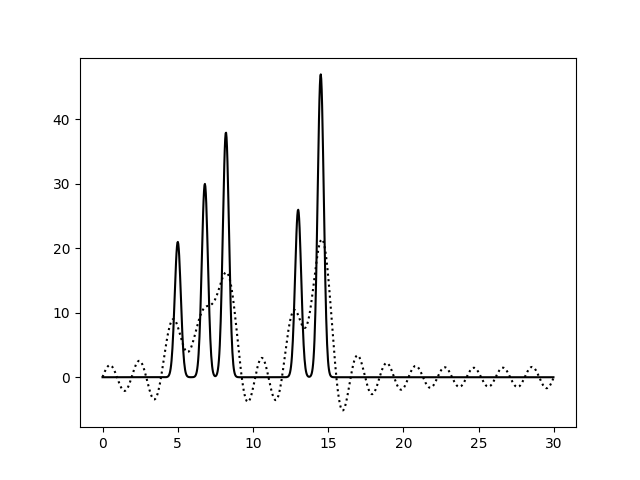
На Рис. 2 показаны функции электронной плотности, восстановленные по 0 - 5, 0 - 10, 0 - 15, 0 - 20, 0 - 25 и 0 - 30 первым гармоникам, в сравнении с исходной функцией ЭП (сплошная линия). Функции, восстановленные по 0 - 5 и 0 - 10 гармоникам, не позволяют определить положения атомов (плохое восставновление). Функция по 0 - 15 гармоникам уже позволяет угадать положения атомов, кроме второго и третьего в первой молекуле (среднее восстановление). При использовании 0 - 20 и 0 - 25 гармоник функция ЭП четко определяет положения всех атомов, но шумовые пики могут быть сравнимы с небольшими атомами (хорошее восстановление). И, наконец, функция, восстановленная по 0 - 30 гармоникам, позволяет определить максимумы всех пиков, а уровень шума не вносит смысловые коррективы в определение атомов (отличное восстановление). Номер гармоники 30 принят за n_0 - при выполнении остальных заданий для восстановления функции ЭП будет использоваться набор гармоник 0 - 30.
| Диапазон гармоник | 0 - 10 | 0 - 10 | 0 - 15 | |
 |
 |
 |
||
| Диапазон гармоник | 0 - 20 | 0 - 25 | 0 - 30 | |
 |
 |
 |
Влияние внесения шума в значения амплитуд и фаз гармоник
Наше моделирование позволяет нам рассмотреть закономерности, далекие от реальности. В реальных данных всегда присутствует шум, поэтому важно определить влияние шума на функцию ЭП. В нашей модели внесение m % шума к амплитудам (параметр -F <число> в скрипте func2fourier.py) и/или фазам (-P <число>) равносильно прибавлению к каждому значению амплитуды/фазы числа, распределенного нормально со средним 0 и среднеквадратичным отклонением σ = 0.2*m.
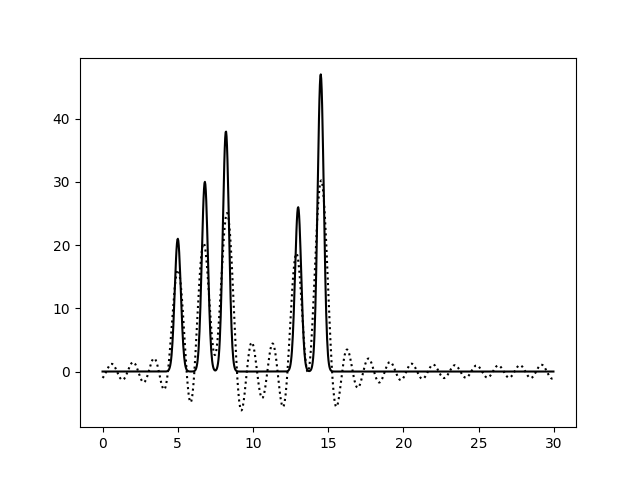
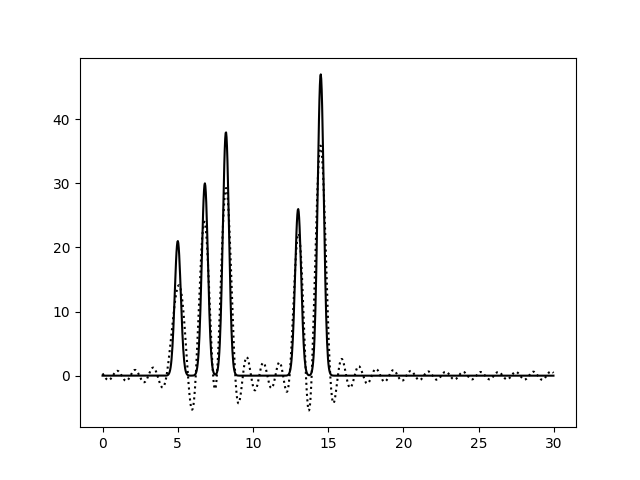
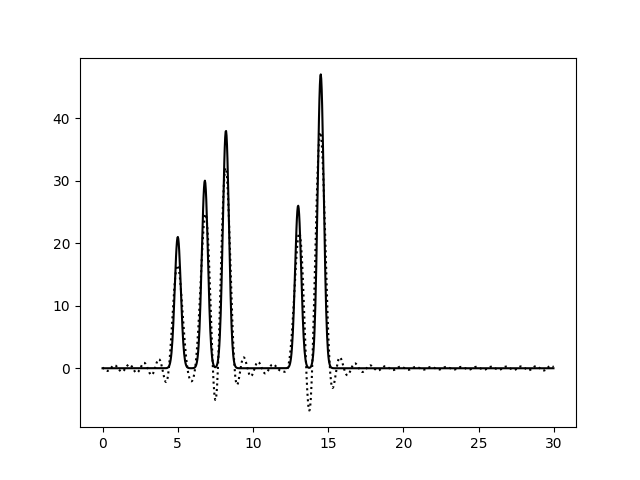
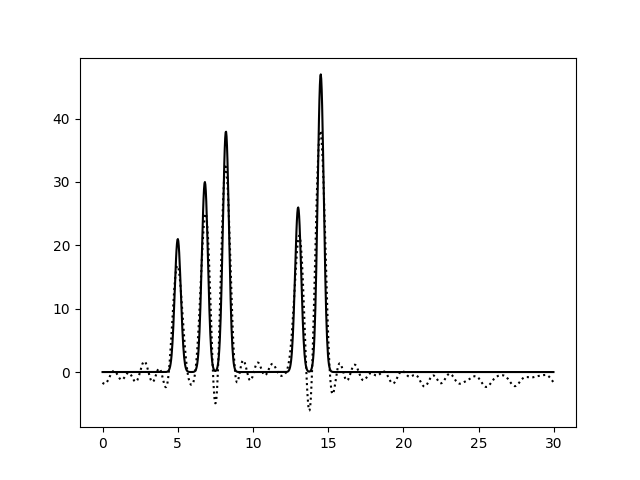
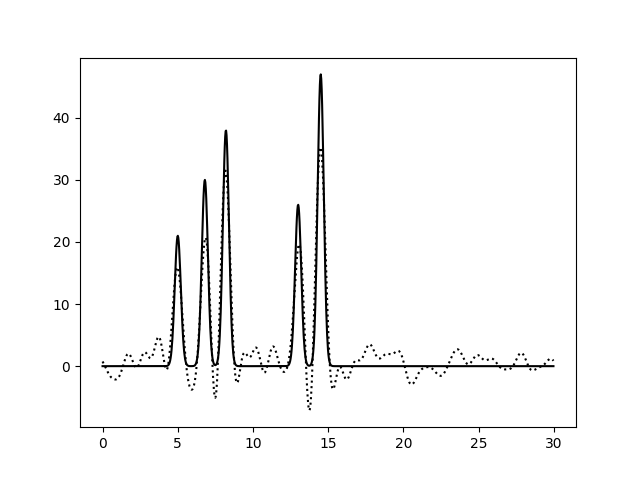
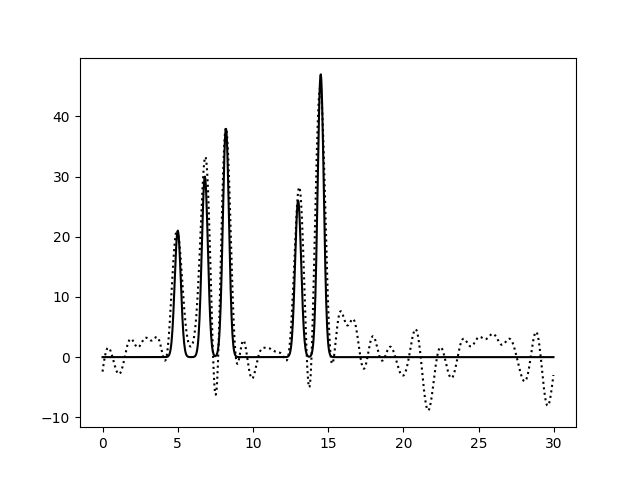
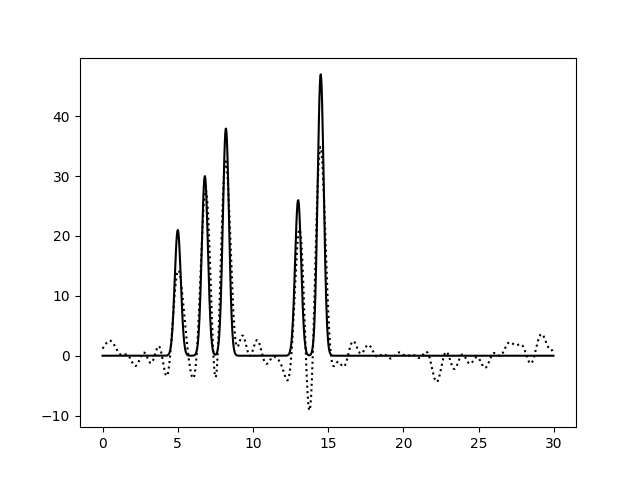
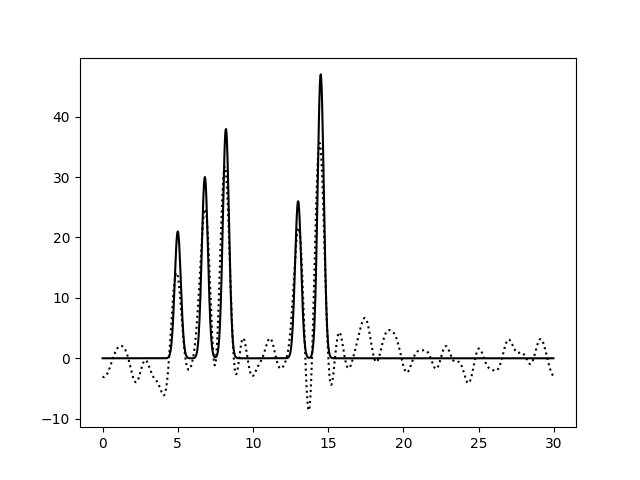
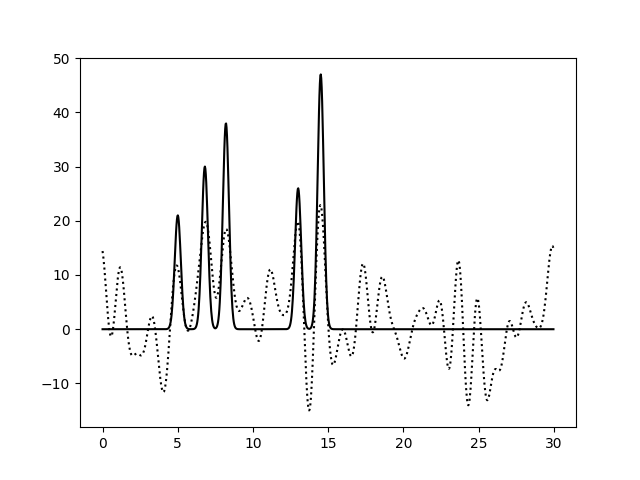
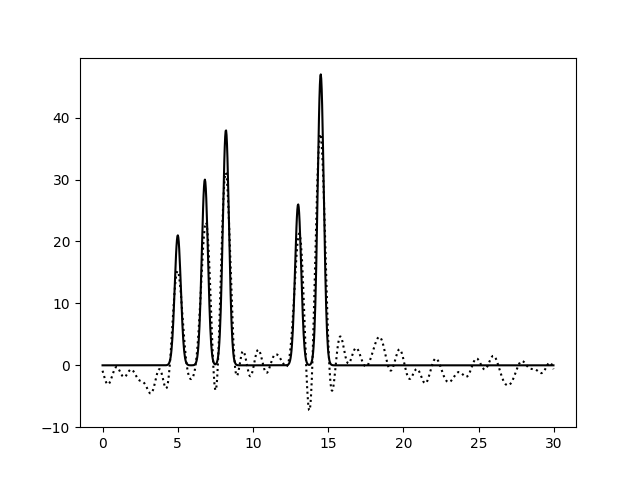
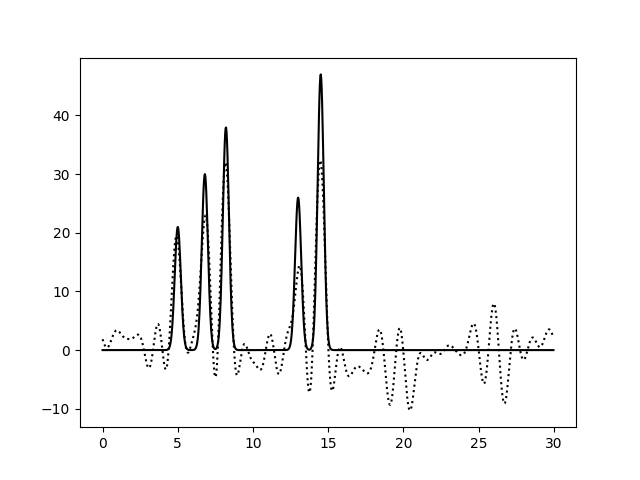
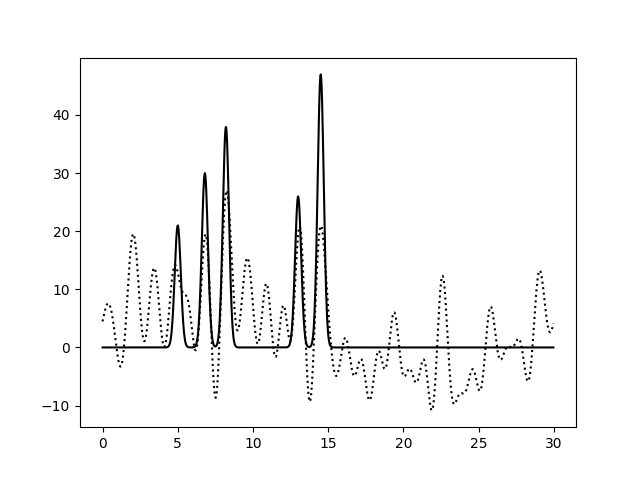
На Рис. 3 изображены функции ЭП, восстановленные после добавления 10, 25 и 50% шума к амплитудам, фазам и обоим параметрам гармоник сразу. Влияние шума при 10% можно считать незначительным для всех вариантов. При больших уровнях шума видим, что шум в фазах влияет гораздо сильнее: шумовые пики выше, а максимумы для исходных атомов ниже, вообще весь график смещается вниз по вертикальной оси. При добавлении 50% шума к амплитудам, максимумы для атомов можно различить (хорошее восстановление), а добавление 50% шума к фазам уже не позволяет отличить правильные пики от шума. Внесение шума для обоих признаков одновременно усиливает влияние каждого из шумов и подтверждает, что больший эффект на восстановление функции ЭП оказывает шум в фазах (при 50% шума поведение функции ЭП совпадает для шума в фазах и совместного шума).
| Шум, % | 10 | 25 | 50 |
| F |
 |
 |
 |
| P |
 |
 |
 |
| F & P |
 |
 |
 |
Влияние неполноты набора гармоник на восстановление функции ЭП
По результатам экспериментов чаще всего наборы гармоник содержат пропуски. Пропуски в разных местах набора могут оказывать разное влияние на восстановление функции ЭП.
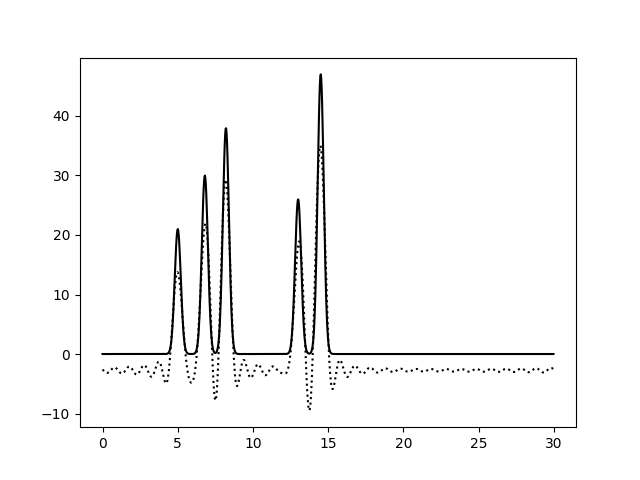
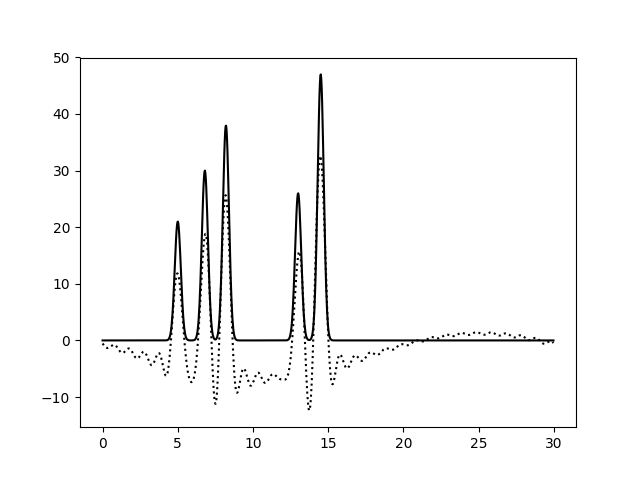
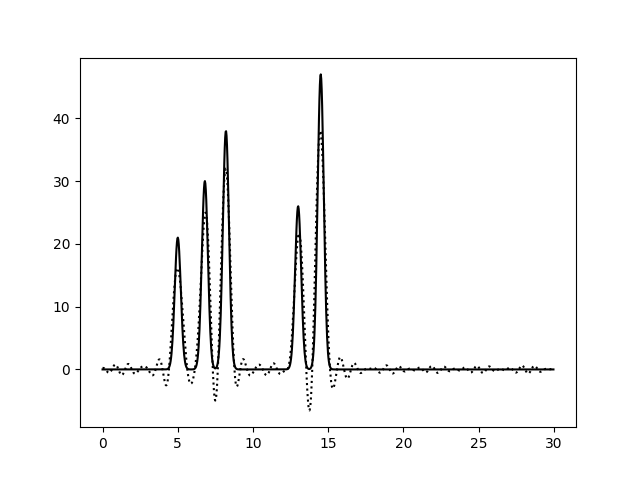
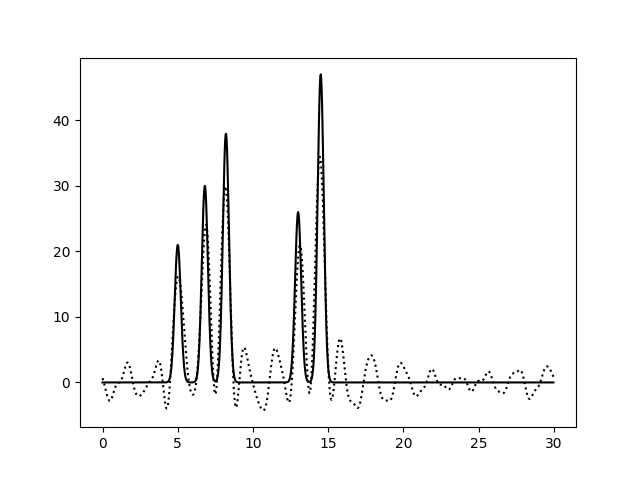
На Рис. 4 показаны графики функции ЭП, восстановленной по неполным наборам гармоник. При исключении гармоники с номером 0 (1 - 30) график опускается вниз, так как первая гармоника - константа, она просто вычитается из исходной функции. Вторая гармоника (номер 1) - синусоида, что мы и видим при исключении гармоник 0 - 1. При этом уровень шума незначительный, ничто не мешает определять правильные пики.
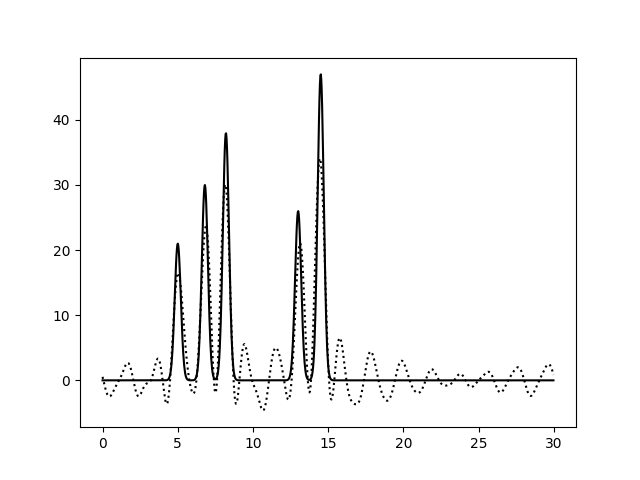
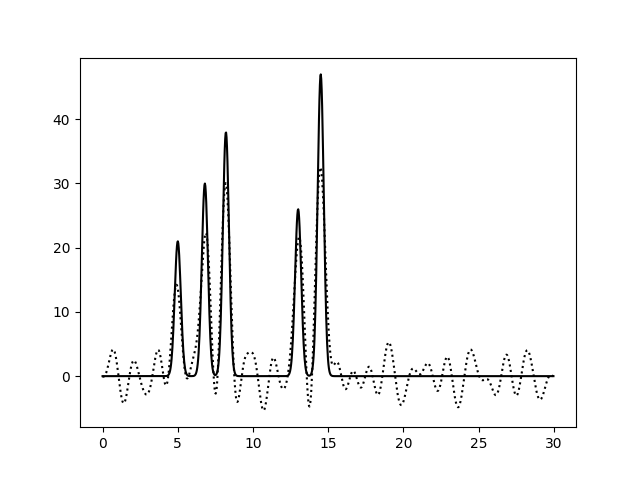
При исключении гармоник из середины набора шум уже достаточно сильный. А добавление гармоники с номером 40 (на 10 больше, чем n_0) не влияет на восстановление функции ЭП ни для набора без пропусков (0 - 30, 40), ни для набора с уже имеющими пропусками (0 - 12, 16 - 30, 40). Таким образом, наибольшее влияние оказывают пропуски в середине набора гармоник.
| Диапазон гармоник | 1 - 30 | 2 - 30 |
 |
 |
|
| Диапазон гармоник | 0 - 12, 16 - 30 | 0 - 9, 11 - 15, 17 - 22, 24 - 30 |
 |
 |
|
| Диапазон гармоник | 0 - 30, 40 | 0 - 12, 16 - 30, 40 |
 |
 |
В качестве вывода можно повторить, что на восстановление функции электронной плотности наибольшее влияние оказывают шумы в значениях фаз и пропуски в середине набора гармоник.
Информация обо всех восстановлениях функции ЭП приведена в Таблице 1. Отдельного комментария заслуживают колонки "Разрешение" и "Полнота". Для полного набора гармоник разрешение - наименьшее из разрешений (периодов) входящих в него гармоник. Гармоники упорядочены таким образом, что чем больше ее номер, то тем меньше ее период, и, следовательно, тем меньше (лучше) ее разрешение. В нашем случае для полного набора из гармоник с номерами 0 - n разрешение набора вычислялось как 30/n (n - самый большой номер гармоники в наборе). При подсчете разрешения неполных наборов гармоник действует та же логика, но нужно еще указывать значение полноты - доли измеренных гармоник с разрешением равным или большим того, которое выбрано как разрешение набора, от всех возможных гармоник на этом отрезке. Вариации проистекают из соображений того, что по стандартам полнота должна быть не меньше 90%. То есть для неполного набора гармоник, где n - номер последней гармоники в наборе, если полнота при подсчете разрешения как <длина отрезка>/n меньше 90%, то можно исключать гармоники с номерами n и меньше, пока не получим полноту не меньше 90%, и для такого набора посчитаем разрешение.
Пример: набор гармоник 0 - 12, 16 - 30, 40. Можно сказать, что его разрешение 0,75 Å, но тогда полнота будет 70,7%. Или можно исключить из набора гармонику с номером 40, тогда разрешение будет 1 Å, зато полнота станет 90,3%. В Таблице 1 для наборов гармоник, чья полнота составила менее 90%, если считать разрешение набора как период гармоники с номером n, приведен альтернативный вариант подсчета разрешения, чтобы полнота соответствовала стандартам.