Филогенетическое устройство отобранных бактерий
Для работы было выбрано  дерево белков бактерий, построенное при помощи JalWiev (соседство по весу BLOSUM62). После чего при помощи программы fretree из пакета программ EMBOSS исследуемое дерево
дерево белков бактерий, построенное при помощи JalWiev (соседство по весу BLOSUM62). После чего при помощи программы fretree из пакета программ EMBOSS исследуемое дерево  было укоренено в среднюю точку.
было укоренено в среднюю точку.
Полученое дерево представлено на Рисунке 1. Визуализация проводилась программой fdrawgram из пакета EMBOSS. Дерево укоренено в ветвь {'RS2_BACAN', 'RS2_CLOB1', 'RS2_GEOKA', 'RS2_LISMO', 'RS2_STAA1'}vs{'RS2_LACAC', 'RS2_FINM2', 'RS2_ENTFA'}, данное укоренение можно считать правильным, т.к. при переукоренении в среднюю точку программой fretree на вход был подан файл в формате nwk с прописанными длинами ветвей.

Рисунок 1. Филогенетическое дерево, построенное по алгоритму объединения соседей (по BLOSUM62), укорененное в среднюю точку программой fretree из пакета EMBOSS
Использование внешней группы
Для работы в качестве внешней группы был выбран белок RS2_ECOLI, после чего  последовательности белков были
последовательности белков были  выровнены по алгоритму t-coffe.
выровнены по алгоритму t-coffe.
После по полученному выравниванию было построено  филогенетическое дерево по алгоритму максимальной правдоподобности в программе MEGA, с укоренением при помощи внешней группы (укоренение прошло в ветвь {'BACAN', 'LACAC', 'GEOKA', 'LISMO', 'ENTFA', 'STAA1'}vs{'CLOB1', 'FINM2'} ). Полученное дерево представлено на Рисунке 2. От правильного филогенетического дерева, представленного в позапрошлом практикуме полученное различается топллогической организацией некоторых клад, что говорит о том, данная внешняя группа оказывает влияние на получение филогенетических данных, хотя укоренение прошол верно (так же как в правильном дереве).
филогенетическое дерево по алгоритму максимальной правдоподобности в программе MEGA, с укоренением при помощи внешней группы (укоренение прошло в ветвь {'BACAN', 'LACAC', 'GEOKA', 'LISMO', 'ENTFA', 'STAA1'}vs{'CLOB1', 'FINM2'} ). Полученное дерево представлено на Рисунке 2. От правильного филогенетического дерева, представленного в позапрошлом практикуме полученное различается топллогической организацией некоторых клад, что говорит о том, данная внешняя группа оказывает влияние на получение филогенетических данных, хотя укоренение прошол верно (так же как в правильном дереве).
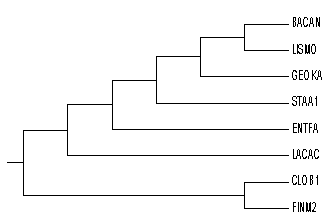
Рисунок 2. Филогенетическое дерево, построенное по алгоритму максимального правдоподобия в программе MEGA, укорененное при помощи внешней группы (E.coli).
Бутстрэп
Для бутстрэп анализа было выбрано дерево построенное по алгоритму объединения соседей (выравнивание по BLOSUM62) (представлено на Рисунке 1), количество реплик 100. Результат бутстрэп анализа представлен на Рисунке 3.
Полученное консенсусное дерево не отличается от исходного, отличия которого от правильного филогенетического дерева:
Нетривиальные ветви правильного дерева
{'BACAN', 'GEOKA'}vs{'FINM2', 'LACAC', 'ENTFA', 'STAA1', 'CLOB1', 'LISMO'}
{'CLOB1', 'FINM2'}vs{'BACAN', 'GEOKA', 'LACAC', 'ENTFA', 'STAA1', 'LISMO'}
{'BACAN', 'GEOKA', 'LISMO'}vs{'LACAC', 'CLOB1', 'ENTFA', 'STAA1', 'FINM2'}
{'ENTFA', 'LACAC'}vs{'BACAN', 'GEOKA', 'FINM2', 'STAA1', 'CLOB1', 'LISMO'}
{'BACAN', 'GEOKA', 'LISMO', 'STAA1'}vs{'LACAC', 'CLOB1', 'ENTFA', 'FINM2'}
Нетривиальные ветви полученного дерева
{'BACAN', 'GEOKA'}vs{'FINM2', 'LACAC', 'ENTFA', 'STAA1', 'CLOB1', 'LISMO'}
{'BACAN', 'CLOB1', 'GEOKA'}vs{'LACAC', 'LISMO', 'ENTFA', 'STAA1', 'FINM2'}
{'BACAN', 'CLOB1', 'ENTFA', 'GEOKA', 'LISMO', 'STAA1'}vs{'LACAC', 'FINM2'}
{'BACAN', 'CLOB1', 'GEOKA', 'LISMO'}vs{'LACAC', 'ENTFA', 'STAA1', 'FINM2'}
{'BACAN', 'CLOB1', 'GEOKA', 'LISMO', 'STAA1'}vs{'LACAC', 'ENTFA', 'FINM2'}
Ветви которые есть в правильном дереве, но отсутствуют в полученном
{'CLOB1', 'FINM2'}vs{'BACAN', 'GEOKA', 'LACAC', 'ENTFA', 'STAA1', 'LISMO'}
{'BACAN', 'GEOKA', 'LISMO', 'STAA1'}vs{'LACAC', 'CLOB1', 'ENTFA', 'FINM2'}
{'BACAN', 'GEOKA', 'LISMO'}vs{'LACAC', 'CLOB1', 'ENTFA', 'STAA1', 'FINM2'}
{'ENTFA', 'LACAC'}vs{'BACAN', 'GEOKA', 'FINM2', 'STAA1', 'CLOB1', 'LISMO'}
Ветви которые есть в полученном дереве, но отсутствуют в правильном
{'BACAN', 'CLOB1', 'ENTFA', 'GEOKA', 'LISMO', 'STAA1'}vs{'LACAC', 'FINM2'}
{'BACAN', 'CLOB1', 'GEOKA', 'LISMO'}vs{'LACAC', 'ENTFA', 'STAA1', 'FINM2'}
{'BACAN', 'CLOB1', 'GEOKA'}vs{'LACAC', 'LISMO', 'ENTFA', 'STAA1', 'FINM2'}
{'BACAN', 'CLOB1', 'GEOKA', 'LISMO', 'STAA1'}vs{'LACAC', 'ENTFA', 'FINM2'}
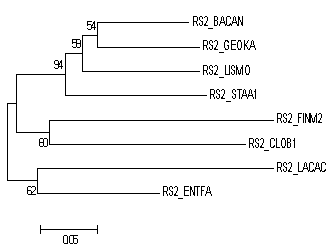
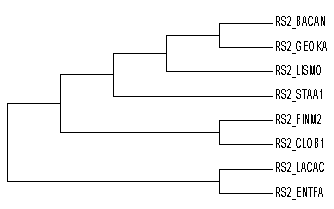
Рисунок 3. Филогенетическое дерево, построенное по алгоритму объединения соседей (выравнивание по BLOSUM62) (слева), и проанализированное при помощи бутстрэпа (справа).
