Восстановление функции по коэффициентам ее ряда Фурье



Задача

Симулировать эксперимент по получению данных об амплитудах и фазах гармоник Фурье и восстановить по ним функцию ЭП.

Симуляция эксперимента

Для симуляции использовалась модель одномерной электронной плотности. На отрезке от 0 до 30 (ангстрем) задается функция, имеющая вид нескольких гауссовых кривых с различными параметрами. Эти кривые, представляющие собой пики на графике, соответствуют электронным плотностям атомов. Атомы одной молекулы, связанные ковалентно, расположены на расстоянии 1-1.5 ангстрема. Отдельные молекулы расположены на расстоянии 3-5 ангстрем, что соответствует водородным или гидрофобным взаимодействиям. Параметры гауссовских кривых соответствуют различным атомам. Различная высота пиков соответствует различному количеству электронов в атоме, ширина пика примерно соответствует диаметру атома, то есть должна быть порядка 1 ангстрема.
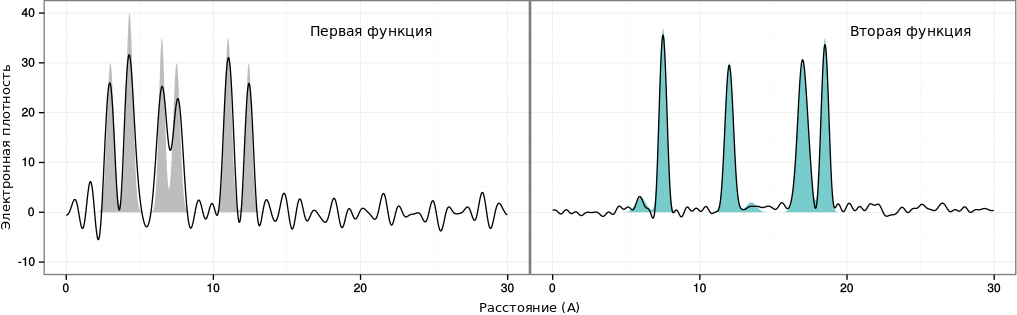
В работе использовалось две функции. Первая содержала только "большие" атомы, во вторую были включены "маленькие атомы", обладающие намного меньшей высотой. Дисклемер: подчеркиваю, что в работе не проводится никаких параллелей с этими гипотетическими атомами и атомами углерода, водорода или какого-либо другого элемента. Как оказалось, вид исходной функции сильно сказывается на результатах симуляции с различными параметрами. В обоих случаях функция содержала в себе шесть пиков.


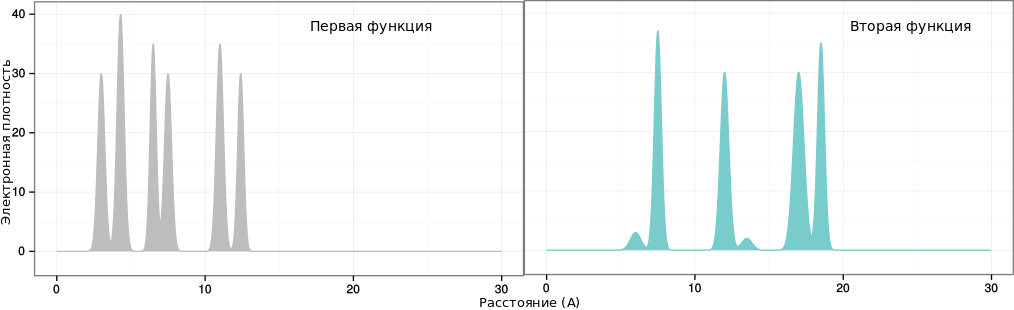Рис. 1: Одномерные функции электронной плотности

Эта функция была создана с помощью скрипта compile-func.py с параметрами:


Каждое "слагаемое" в формуле для параметра -g соответствует одному атому (пику). Слагаемые содержат в себе параметры, разделенные запятыми. Первое число - высота пика (число электронов), второе задает ширину пика (размер атома) и последнее - положение пика на прямой (одномерное пространство, в котором происходит симуляция ЭП). Один из пиков, маленький, соответствует атому водорода. Он существенно усложнил восстановление электронной плотности, что будет показано в работе.

Таким образом задается функция электронной плотности, но она не является данными эксперимента. Непосредственно информацией, которую получает исследователь, являются данные об амплитудах и фазах гармоник Фурье. Скрипт func2fourier.py симулирует эксперимент, в результате которого высчитываются указанные гармоники ряда Фурье, амплитуды и фазы. Кроме того, можно задавать шум для амплитуды и фазы, что приближает условия эксперимента к реальным.
В результате входными данными для анализа является файл вида


#no.    F       phi
0       4.11603172044   0.0
1       1.29412362899   2.33767564681
2       1.74223751844   2.50453110776
3       0.748523767261  -2.55855339062

Восстановление функции электронной плотности

Для выполнения работы (в том числе вызова однотипных функций с различными параметрами) был написан единый скрипт. Для каждой части работы будет приведена его соответствующая часть на примере первой функции.


1. Полные наборы гармоник


Для описанных выше функций строились графики восстановленной функции по полному набору гармоник до n0, на котором восстановление было отличным. Графики показывались человеку, который не знал изначальной функции, и по тому, как он мог определить атомы, и определялось качество восстановления.

Графики четырех соответствующих восстановленных функций для модели, не содержащей водороды, показаны на рис. 2. Довольно хорошо видно, где находятся атомы, даже при малом количестве гармоник, и главной проблемой становится разрешение соседних пиков.


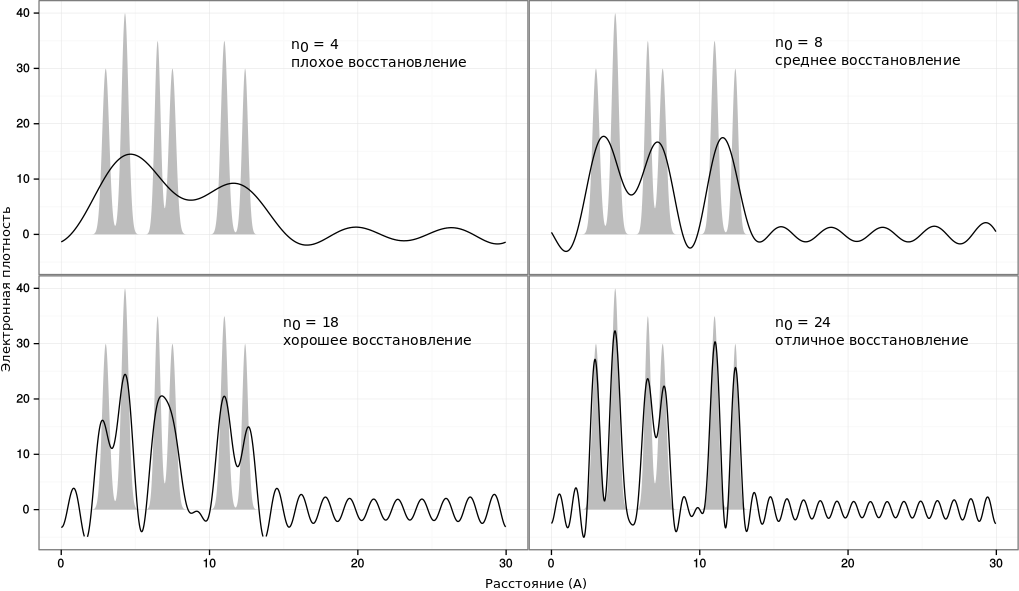Рис. 2: Восстановление первой функции полным набором гармоник

Для отличного восстановления второй функции, содержащей низки пики, требуется больше гармоник. Большие пики различимы и при меньшем разрешении, но маленькие сливаются с шумом, и опеределить местонахождение их максимумов сложнее (рис. 3).


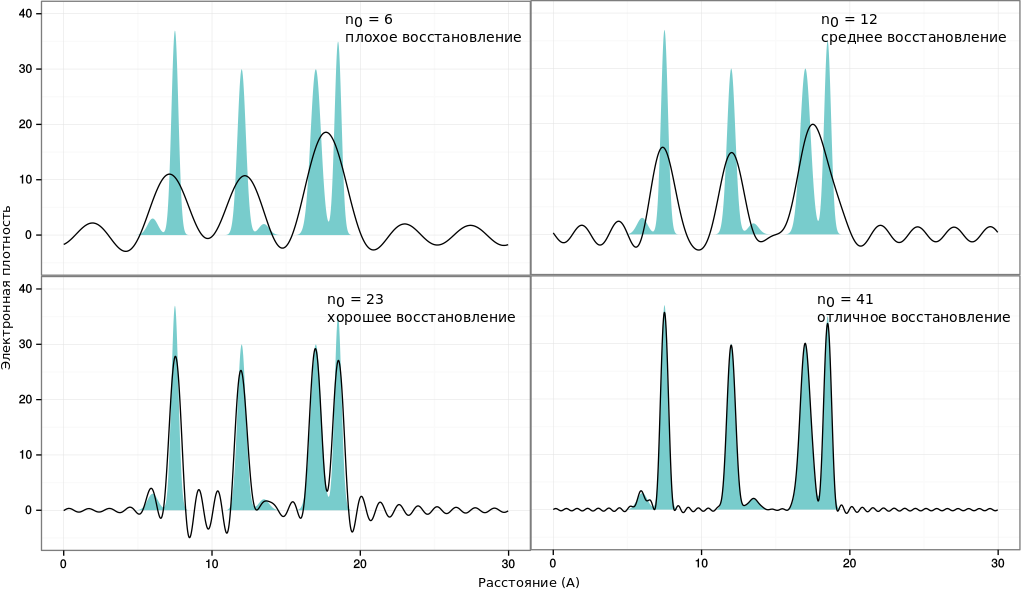Рис. 3: Восстановление второй функции полным набором гармоник

В табл. 1 приведены сводные результаты симуляции.


Функция
Восстановление (значение n0)
Разрешение n0
отличного
восстановления
ПлохоеСреднееХорошееОтличное
Первая4818261.15 A
Вторая61223410.73 A


Скрипт:


g='30,3,3+40,3,4.3+35,3.5,6.5+30,3,7.5+35,3,11+30,3.5,12.4'

python compile-func.py -g $g -o func.txt   
n=30
python func2fourier.py -i func.txt -o fourier.txt -F 0 -P 0
for (( i=0; i<=n; i+=1 ))
do
python fourier-filter.py -i fourier.txt -o fourier${i}_filter.txt -r 0-${i}
python fourier2func.py -f func.txt -i fourier${i}_filter.txt -o re_func${i}.txt -s 
done
fi


2. Полные наборы гармоник + шум


Следующий шаг - оценка качества восстановления в зависимости от шума амплитуды или фазы. По полному набору гармоник (0, 1, ..., 26 для первой функции и 42 для второй) были построены графики восстановленной функции при разных значениях шума. Некоторые из полученных графиков представлены ниже. Эти же данные внесены в финальную таблицу (в конце отчета).



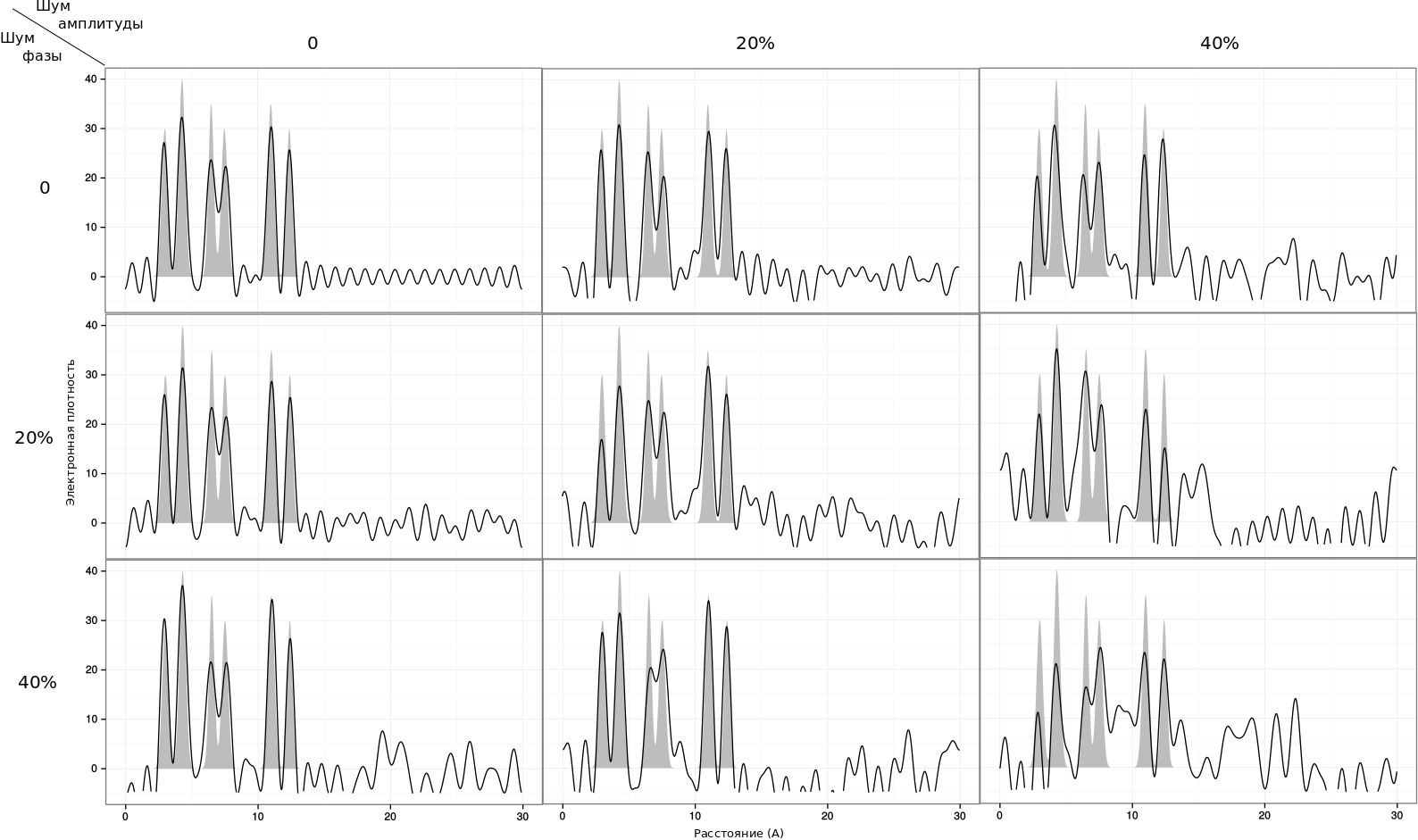Рис. 4: Восстановление первой функции при добавлении шума


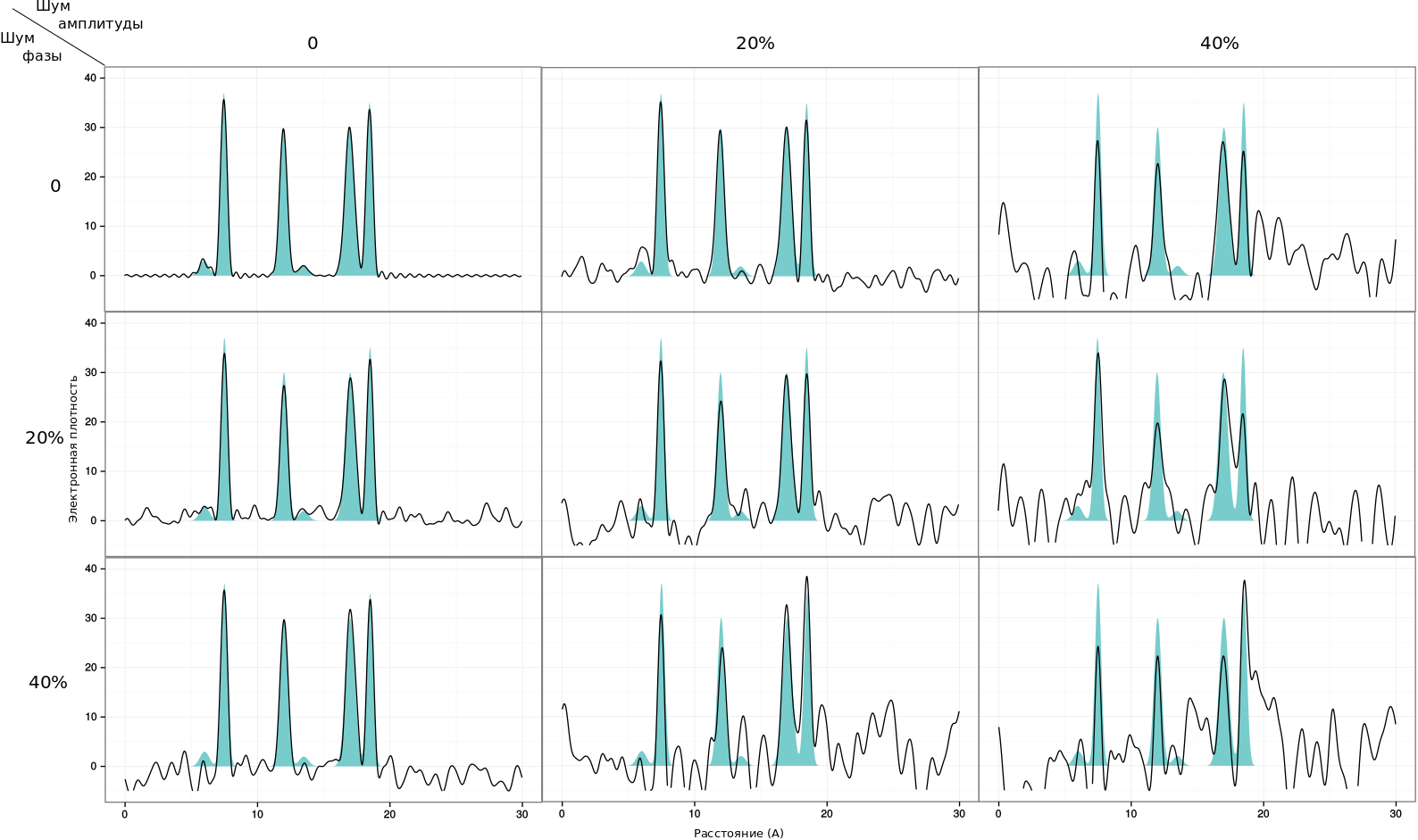Рис. 5: Восстановление первой функции при добавлении шума

Для первой функции, содердащей только высокие пики, шум не препятствует определению местонахождения "атомов" влоть до значения шума в 40% для обоих параметров, причем при шуме амплитуды близкие пики начинают сливаться, а ошибочные пики достигают высоты "правильных". Для определения маленьких пиков во второй функции большее значение имеет точность оределения фазы, так как появляющиеся небольшие ошибочные пики сливаются с настоящими, а при большой ошибке в амплитуде еще и достигают высоты, гораздо большей, чем значение настоящих максимумов.

Становится ясным, как важно решить проблему фаз в реальном эксперименте, так как неверное определение фазы действительно может сильно повлиять на результат анализа.

Скрипт:


noise=60
for (( i=0; i<=$noise; i+=20 ))
do
for (( j=0; j<=$noise; j+=20 ))
do
python func2fourier.py -i func.txt -o fourier_n_${i}_${j}.txt -F ${i} -P ${j}
python fourier-filter.py -i fourier_n_${i}_${j}.txt -o fourier_filter_n_${i}_${j}.txt -r 0-${n}
python fourier2func.py -f func.txt -i fourier_filter_n_${i}_${j}.txt -o re_func_n_${i}_${j}.txt
done
done


3. Удаление начальных гармоник


Нужно понять, как первые гармоники влияют на качество результата. Для этого были удалены первые гармоники (0 и 0-1) и оценено качество восстановления функции. В этой и последующих симуляциях использовались уровни шума для фазы и амплитуды, равные 5%.


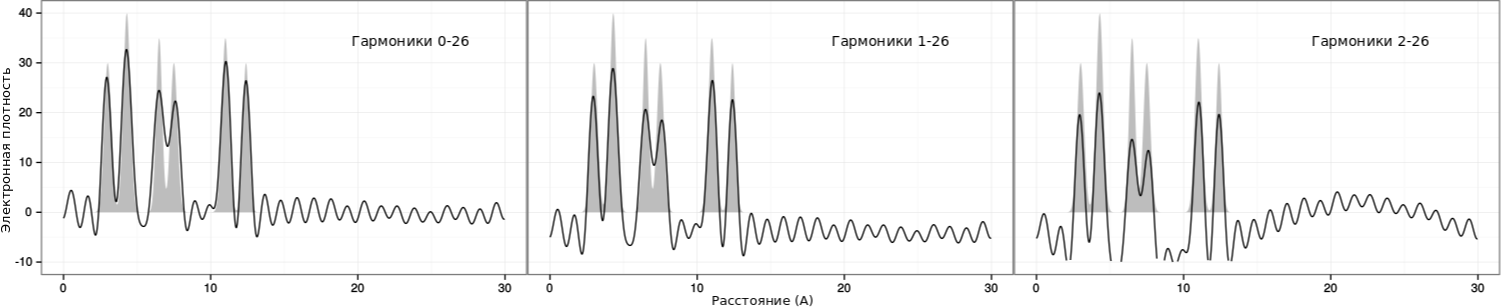Рис. 7: Восстановление первой функции без начальных гармоник


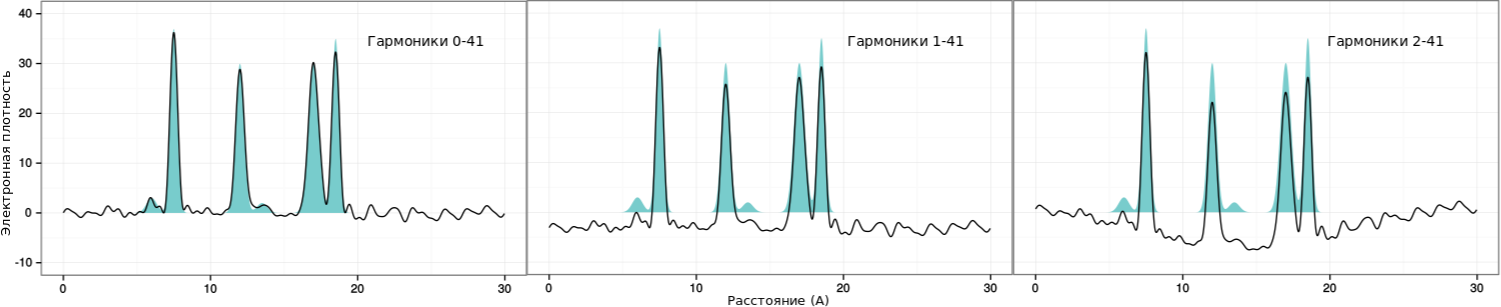Рис. 8: Восстановление второй функции без начальных гармоник

При удалении первых гармоник значительно "нарушается" фоновое значение (оно уже явно не похоже на прямую). Однако распознавание пиков не затрудняется по сравнению с полным набором гармоник, кроме того, вероятно, фоновую "кривую" можно выровнить.
Скрипт:>


python func2fourier.py -i func.txt -o fourier_n_5.txt -F 5 -P 5
for (( i=0; i<=2; i++ ))
do
python fourier-filter.py -i fourier_n_5.txt -o fourier_filter_delinit_${i}.txt -r ${i}-${n}
python fourier2func.py -f func.txt -i fourier_filter_delinit_${i}.txt -o re_func_delinit_${i}.txt
done


4: Удаление части гармоник из середины набора


Следующей задачей было посмотреть, как искажается восстановленаня функция при удалении 5 и 10% гармоник из середины набора (для первой функции удалялись гармоники 10 и 16 (~5%), 13 (~10%), для второй — 15, 25 (~5%), 18, 23 (~10%)).


Рис. 8: Восстановление первой функции неполным набором гармоник


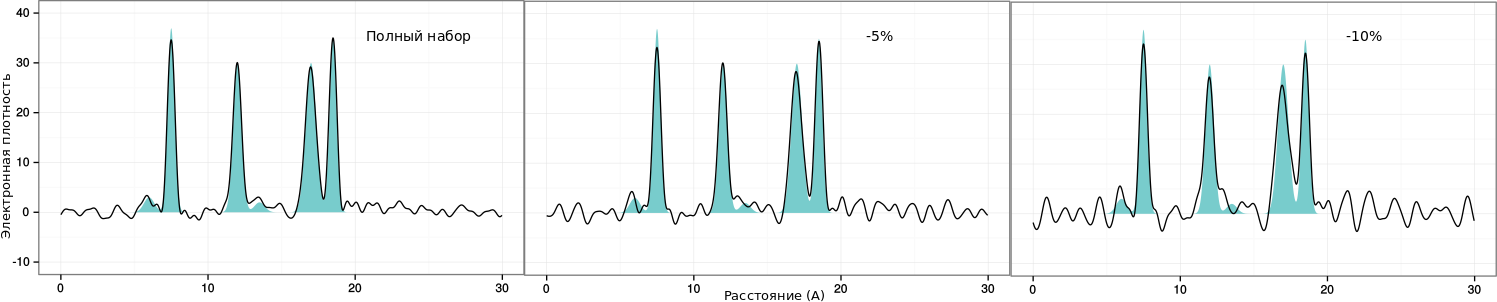Рис. 9: Восстановление второй функции неполным набором гармоник

Как видно на рис. 8 и 9, хотя неполнота набора гармоник и снижает разрешение, все равно легко определить высокие пики. Пики атомов водорода же сливаются с соседними и смещаются.

Скрипт:


python fourier-filter.py -i fourier_n_5.txt -o fourier_filter_del5.txt -r 0-9,11-15,17-26
python fourier2func.py -f func.txt -i fourier_filter_del5.txt -o re_func_del5.txt
python fourier-filter.py -i fourier_n_5.txt -o fourier_filter_del10.txt -r 0-9,11-12,14-17,19-26
python fourier2func.py -f func.txt -i fourier_filter_del10.txt -o re_func_del10.txt


5


К наборам гармоник были добавлены гармоники с номерами 36 и 51, соответственно (рис. 10).


Рис. 10: Добавление гармоники с высоким разрешением

Хотя разрешение добавленной гармоники выше, чем у остальных, из-за получившейся сильной неполноты набора гармоник она несильно влияет на фактическое разрешение набора.


Скрипт:


python fourier-filter.py -i fourier_n_5.txt -o fourier_filter_add10.txt -r 0-$n,$(($n + 10))
python fourier2func.py -f func.txt -i fourier_filter_add10.txt -o re_func_add10.txt

6

В табл. 1 представлены результаты симулированных экспериментов. Для функции с "атомами водорода" качество швосстановления определялось именно с учетом этих атомов (если смотреть только на большие пики, качество определения структур чаще всего остается отличным). В колонку "разрешение" при наличии сильного шума вписывалось реальное разрешение (детали на расстоянии d/2 различимы).


Таблица 1.

Набор гармоникРазрешение (Å)Полнота данных (%)Шум амплитуды (%)Шум фазы (%)Качество восстановленияКомментарии
Первая функция (только большие пики)
Полный набор гармоник
0-47.510000Плохое
0-83.7510000Среднее
0-181.6710000Хорошее
0-261.1510000Отличное
0-26 > 1.9100400ХорошееРазрешение макс. гармоники 1.15
0-26 > 2100040ХорошееРазрешение макс. гармоники 1.15
0-26 > 2.21004040СреднееРазрешение макс. гармоники 1.15
Неполный набор гармоник
1-261.159655Отличное
2-261.159355Отличное
0-9,11-15,17-26~ 1.59355ОтличноеРазрешение макс. гармоники 0.81
0-9,11-12,14-17,19-26> 28855ОтличноеРазрешение макс. гармоники 0.81
0-26,361.15 (до 26 гармоники)73 (до 26 гармоники - 100)55ОтличноеРазрешение макс. гармоники 0.81
Вторая функция (маленькие пики)
Полный набор гармоник
0-65.0010000Плохое
0-122.5010000Среднее
0-231.3010000Хорошее
0-410.7310000Отличное
0-41 > 1100400СреднееРазрешение макс. гармоники 1.15
0-41 > 1.5100040СреднееРазрешение макс. гармоники 1.15
0-41 > 1.51004040СреднееРазрешение макс. гармоники 1.15
Неполный набор гармоник
1-410.739855Хорошее
2-410.739555Хорошее
0-14,16-24,26-41~ 19555Хорошее
0-14,16-17,19-22,24,26-41~ 1.59055Среднее
0-41,510.73 (до 41 гармоники)81 (до 41 гармоники - 100)55ХорошееРазрешение макс. гармоники 0.73

7


Как видно, фактическое разрешение зависит от полноты набора гармоник. Для полного набора его разрешение имеет смысл определять как разрешение измереной гармоники с наибольшим номером. Если в наборе пропущено много гармоник с большими номерами, то имеет смысл не учитывать несколько наибольших до какого-то порога полноты (вероятно, он должен составить 90-95%). Если же пропущено большое количество гармоник в середине набора, разрешение тоже падает, но просто выкидывание несколько гармоник уже не поможет. Для этого случая мне трудно придумать универсальное правило, которое могло бы подойти для самых разных ситуаций.


8. Выводы




Таблица