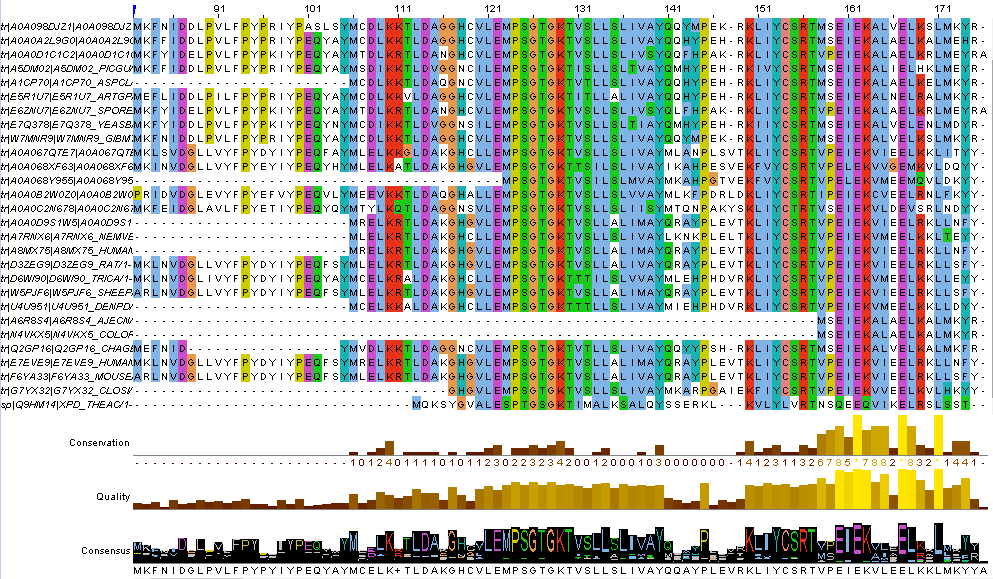
Блок 4: домены белкаЗадание 1В базе pfam.xfam.org было найдено семейство HBB (идентификатор в базе: PF06777). Белки семейства входят в качестве доменов в ДНК-репарирующие хеликазы эукариот. Хеликаза формирует тороидальную структуру для разделения цепей ДНК и поиска повреждений, а HBB-домен помогает зажимать ДНК. Если хеликаза обнаруживает повреждение, запускается механизм репарации. Для семейства HBB существует 17 доменных архитектур в 492 последовательностях у 450 особей. Для оценки были выбраны архитктуры:
Скачивать выравнивание из базы JalView отказался (при полной работоспособности других сетевых сервисов навроде muscle и даже после попытки скачать предлагаемый программой пример AC PF03760), поэтому файл с выравниванием всех последовательностей домена был получен непосредственно с pfam.org и покрашен в JalView (проект JalView).
Далее с помощью скрипта Файл с последовательностями домена из uniprot (осторожно, 2,5Мб текста)был подан на вход скрипту
Также к выборке была добавлена последовательность XPD_THEAC, для которой есть 3D-структура. Идентификаторы были собраны в текстовый файл, переданный в retieve/ID mapping на uniprot с получением fasta-файла с 31ой отобранной последовательностью. Из выравнивания была удалена последовательность J9DJ02 (Eukaryota/Fungi c (DEAD_2,DEAD_2, HBB, Helicase_C_2)), плохо выровненная с остальными. Последовательности SHEEP и THEKT, несмотря на длинные невыровненные участки, в целом совпадают по архитектуре, поэтому были оставлены.
Выравнивание показало, что второй домен DEAD есть в большинстве последовательностей, хотя в pfam его наличие почему-то не учитывается:
Задание 2Для выполнения второго задания - построения дерева по выравниванию - само выравнивание было немного подправлено: сокращены описания последовательностей и помечены таксоны, а также убрана невыровненная последовательность. Не входящая в отобранные таксоны последовательность XPD_THEAC оставлена для укоренения дерева. Сокращения по таксонам:
Fasta-файл c последовательностями выровнен в MEGA, удалены невыровнявшиеся N- и C-концы. По Fasta-файлу с выравниванием там же и построено дерево по алгоритму максимального сходства. Алгоритмы Neighbor Joining и Minimal Evolution дают ту же топологию. Видно, что разница в архитектуре, найденная pfam, никак не отражается на положении в дереве. Однако домены внутри таксонов оказываются более схожими, чем между ними: млекопитающие оказались в одном районе дерева. 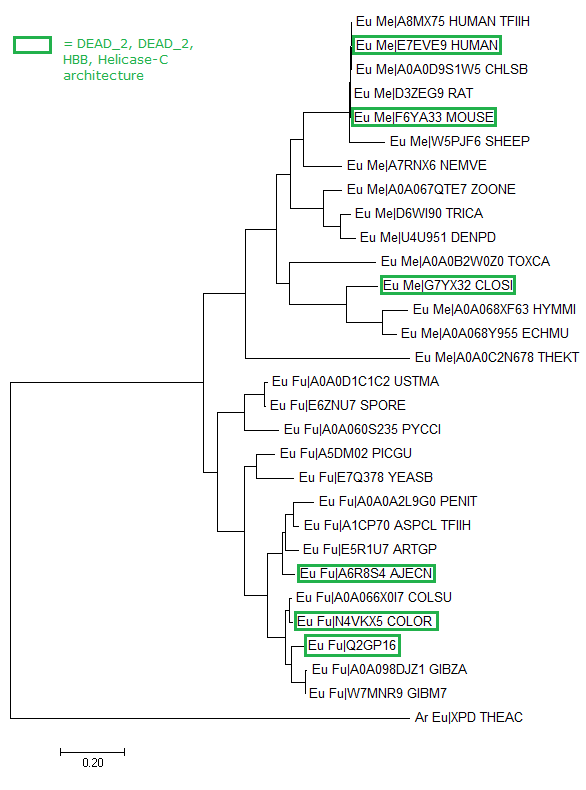 Дерево доступно в Newick-формате
Задание 3Для построения профиля была выбрана клада дерева, отмеченная на рисунке: 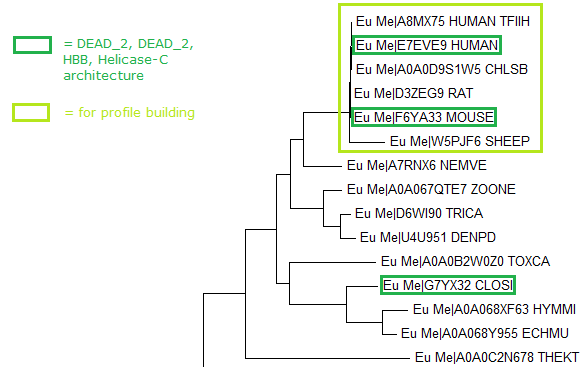 Из выравнивания, использованного при построении дерева в задании 2, получен (копированием нужных участков) файл с 6-ю последовательностями выбранной клады, откуда в JalView были удалены пустые (где были только гэпы) столбцы. Fasta-файл c выравниванием был использован для построения профиля в HMM: hmm2build hmm_built for_profile_cut_and_aligned.fasta, ( построенный профиль)Затем профиль калибруется: hmm2calibrate --histfile hmm_histo hmm_built, ( гистограмма калибровки)После калибровки профиль используется для поиска последовательностей в файле со всеми последовательностями, содержащими семейство PF06777: hmm2search hmm_built PF06777_from_uniprot.fasta > hmm_search, (результаты поиска)Из результатов поиска извлекаются данные по находкам, вставляются в xlsx-файл и упорядочиваются по возрастанию e-value. Для построения ROC-кривой требуется рассчитать чувствительность (отношение числа последовательностей, сочтённых профилями, при том, что они являются профилями, к общему числу профилей, True Positive) и специфичность (отношение числа последовательностей, не сочтённых за профиль, при том, что они профилем и не являются, к общему числу не-профилей, False Negative). Чувствительность для ячейки K считаем как число профилей в ячейках K+1...N, делённое на общее число профилей. Специфичность для ячейки K считаем как число не-профилей в ячейках 1...K, делённое на общее число не-профилей. Потом берём значения (1-специфичность), то есть неспецифичность, в качестве аргумента (ось абсцисс) и строим по ним и значениям чувствительности график: 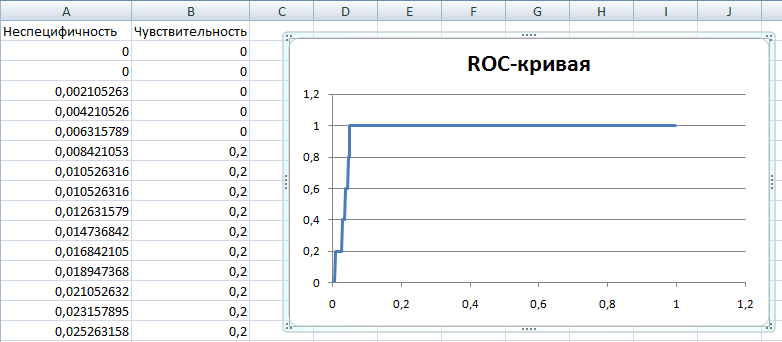 Для граничного e-value по графику была найдена точка выполаживания кривой, однако выяснилось, что это пороговое значение нулевое: точка лежит на последней профильной последовательности F6YA33_MOUSE. То есть из-за малого объёма выборки вероятность ошибки первого рода оказалась очень высокой. Таблица результатов:
|
 (402 последовательности)(
(402 последовательности)( (15 последовательностей).
(15 последовательностей).