Парное выравнивание

Матрицы весов аминокислотных замен

Матрицы весов аминокислотных замен позволяют численно оценить выравнивание. Вес замены амнокислоты на саму себя или на какую-либо другую аминокислоту вычисляется на основе данных о частоте встречаемости каждой замены. Больший вес имеют аминокислотные замены, встречающиеся чаще, чем ожидается. Соответственно, чем больше "удачных" аминокислотных замен в выравнивании, тем больше его вес.

Поскольку консервативность аминокислот обусловлена функцией белка, созданы матрицы весов аминокислотных замен для разных типов белков, например, матрицы BLOSUM и PHAT.

Матрицы BLOSUM вычисляются на основе базы данных BLOCKS, состоящей из множественных выравниваний аминокислотных последовательностей цитоплазматических белков. При вычислении матриц BLOSUM анализируются лишь участки множественных выравниваний, не содержащие гэпов. Для упрощения вычислений анализируемые участки множественных выравниваний могут быть кластеризованы при определённом проценте идентичности (т.е. аминокислотные последовательности, процент идентичности которых не ниже заданного порога, заменяются одной последовательностью). В этом случае порог кластеризации указывается в названии матрицы, например, BLOSUM62. Вычисление матрицы BLOSUM62 на основе обновлённой базы данных BLOCKS можно посмотреть здесь.

Матрицы PHAT вычисляются для мембранных белков.

Сравнение веса замены пролина в цитоплазматических и мембранных белках

Вес замены пролина
	Gly	Pro	Cys	Ser	Thr	Asn	Gln	Asp	Glu	Arg	Lys	Met	Ile	Leu	Val	Ala	Phe	Tyr	Trp	His
	G	P	C	S	T	N	Q	D	E	R	K	M	I	L	V	A	F	Y	W	H
BLOSUM62_new	-2	7	-3	-1	-1	-2	-1	-1	-1	-1	-1	-3	-3	-3	-2	-1	-3	-3	-3	-2
BLOSUM62	-2	7	-3	-1	-1	-2	-1	-1	-1	-2	-1	-2	-3	-3	-2	-1	-4	-3	-4	-2
PHAT_T75_B73	-3	13	-8	-3	-4	-4	-3	-5	-5	-7	-4	-5	-4	-5	-4	-3	-5	-5	-6	-6

Из приведённой выше таблицы видно, что в мембранных белках намного больше пролина, чем в цитоплазматических белках, а также что пролин является консервативной аминокислотой и на какую-либо другую аминокислоту заменяется редко. Скорее всего, это связано со способностью пролина резко изменять направление пептидного остова, вследствие чего замена пролина на какую-либо другую аминокислоту может значительно изменить структуру белка.

В цитоплазматических белках больший вес имеют замены пролина на полярные аминокислоты, т.к. такие замены способствуют изменению структуры и функции белка.

В мембранных белках пролин необходим для формирования множественных α-спиралей и β-складчатых структур, поэтому больший вес имеют замены пролина на неполярные и незаряженные аминокислоты с небольшим радикалом, которые не так сильно изменяют структуру белка.

Сравнение парных выравниваний, построенных вручную и классическими алгоритмами

Сравнение парных выравниваний UVRB_BACSU с его короткими мутантами
Мутант	Выравнивание вручную	Выравнивание алгоритмом Нидлмана-Вунша	Выравнивание алгоритмом Смита-Ватермана
1
1	Identity: 11/21 (52%) Similarity: 13/21 (62%) Score: 54	Identity: 8/665 (1.2%) Similarity: 10/665 (1.5%) Score: 22.5	Identity: 8/20 (40.0%) Similarity: 10/20 (50.0%) Score: 22.5
2
2	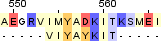Identity: 11/21 (52%) Similarity: 11/21 (52%) Score: 39	Identity: 10/661 (1.5%) Similarity: 10/661 (1.5%) Score: 23	Identity: 5/8 (62.5%) Similarity: 7/8 (87.5%) Score: 26
3
3	Identity: 12/20 (60%) Similarity: 12/20 (60%) Score: 45	Identity: 12/663 (1.8%) Similarity: 12/663 (1.8%) Score: 25	Identity: 11/15 (73.3%) Similarity: 11/15 (73.3%) Score: 29

* Мутанты 1, 2 и 3 были смоделированы с помощью скрипта evolve_protein.pl. Скрипт evolve_protein.pl моделирует эволюцию белка с учётом наследственности и изменчивости (в частности, с учётом возможности замены, делеции и инсерции каждой аминокислоты), но без учёта естественного отбора. При моделировании мутантов были заданы следующие параметры: длина - 20 аминокислот, вероятность изменения аминокислоты и вероятность именно замены аминокислоты в случае её изменения, соответственно:
• для первого мутанта 0.6 и 0.6
• для второго мутанта 0.6 и 0.8
• для третьего мутанта 0.4 и 0.8

** При вычислении Identity и Similarity последовательностей, выровненных вручную, за длину выравнивания принималась длина выровненной последовательности мутанта. При вычислении Score выравниваний вручную штраф за гэпы не назначался. Выравнивания алгоритмом Нидлмана-Вунша были построены в программе needle (запуск со стандартными значениями параметров). Выравнивания алгоритмом Смита-Ватермана были построены в программе water (запуск со стандартными значениями параметров). О программах needle и water можно прочитать здесь.

Из приведённой выше таблицы видно, что выравнивания, построенные классическими алгоритмами в программах needle и water, в большинстве случаев по качеству уступают выравниваниям, построенным вручную. В первую очередь это связано с назначением программами needle и water больших штрафов за открытие гэпа при вычислении Score выравнивания (т.е. программам выгоднее сделать один длинный гэп вместо моделирования точечных делеций и инсерций). Также видно, что для вычисления Identity и Similarity последовательностей с сильно различающейся длиной больше подходит алгоритм Смита-Ватермана, по которому за длину выравнивания принимается длина выровненного участка более короткой последовательности.

Наверх