ПАРНЫЕ ВЫРАВНИВАНИЯ |
Назад |
BLOSUM62 – матрица замен аминокислотных остатков, активно применяющаяся для выравнивания последовательностей белков.
При сопоставлении двух последовательностей необходим критерий качества того или иного выравнивания – парного сопоставления первичной структуры белков, при котором каждому аминокислотному остатку (далее АО или аминокислоты) в одном белке сопоставляется остаток из другого либо пропуск(гэп).
Данная матрица показывает, насколько вероятна замена в ходе мутаций одной аминокислоты на другую. При расчёте вероятности учитывается как статиcтически ожидаемая частота сопоставлений одних АО другим, которая рассчитывается на основе информации о содержании АО во всех белках, так и их реальная частота. Матрица отражает соотношение реальной частоты и статистической. Положительное число напротив того или иного сопоставления говорит, что оно встречается чаще, чем того бы стоило ожидать, если бы последовательности белков выстраивались по математическим, вероятностным законам. Отрицательная, наоборот, показывает, что данное сопоставление маловероятно, даже менее вероятно, чем в том случае, если бы аминокислотные последовательности белков образовывались случайно. Большое положительное число говорит об очень хорошей взаимной заменимости аминокислот, сильно отрицательное же показывает, что эти аминокислоты в ходе эволюции крайне неохотно заменяются друг на друга из-за физико-химических различий. Эта расcчитанная величина называется весом
В рассматриваемой матрице учитываются цитоплазматические белки, которые заметно отличаются от мембранных, в основном за счёт разных долей гидрофобных и гидрофильных аминокислот. Мембраны состоят из липидов, а значит, белки, в них встроенные, будут включать больший процент гидрофобных АО, чем цитоплазматические. Поэтому для них составляют свои матрицы, учитывающие эту особенность.
"62" означает, что эта матрица применяется для белков, у которых идентичность АО составляет не более 62%. Для других процентов есть свои матрицы, что логично, поскольку при разной идентичности белков меняются ожидаемые частоты сопоставлений.
По этой ссылке вы можете посмотреть математические операции, выполняемые над данными о количестве сопоставлений АО в белках при составлении BLOSUM62, а также сравнение весов замены метионина на другие АО в старой матрице, новой составленной и матрице для мембранных белков.
Сравнение матриц аминокислотных замен
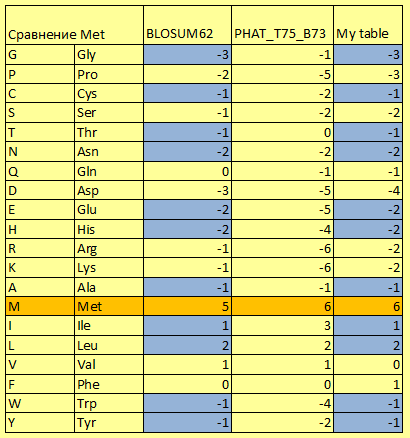 |
В таблице слева приведено сравнение весов замены метио- нина на другие АО согласно общепринятой матрице BLO- SUM62, матрице PHAT для мембранных белков и воссоздан- ной мной матрице BLOSUM62. Синим выделены совпавшие позиции, оранжевым – замена метионина на метионин. Легко заметить, что значения в BLOSUM62 и PHAT действи- тельно сильно отличаются, но даже составленная мной BLO- SUM62 и официальная различаются по почти половине по- зиций, хоть и не так сильно. Различия между двумя BLO- SUM62 можно объяснить разными базами данных, которые применялись при их создании. БД постоянно обновляются и пополняются, из-за чего матрицы, построенные по одной схе- ме, но в разное время, могут в чём-то различаться. Судя по сильно отрицательным цифрам, отрицательно и поло- жительно заряженные аминокислоты крайне неохотно заме- няются на метионин в мембранных белках. Это связано с об- щей малочисленностью заряженных аминокислот в них. С другой стороны, цитоплазматические белки тоже неохотно заменяют метионин на другие + или - аминокислоты, но это связано уже в большей степени с различиями их свойств. Лучше всего метионин меняется на гидрофобные аминокис- лоты, причём предпочтительней на Leu и Ile, вес и размер которых ближе всего к метионину. |
Алгоритмы механическое выравнивание
Для удобства я обрезал исходную последовательность. Подробные сведения о выравниваниях вы можете получить, прочитав этот файл, здесь же я предоставлю лишь результаты в виде сводной таблицы (cм.табл.) и некоторую дополнительную информацию.
Для использования этих алгоритмов можно пользоваться как командной строкой UNIX-систем, так и клиентами с интерфейсом, как например, здесь.
В обоих алгоритмах по умолчанию установлен штраф за открытие гэпа (-10) к весу и (-0.5) за каждый из последующих гэпов, идущих подряд за открывающим.
В рассмотренных случаях программа Needle выдаёт такие же выравнивания, как и при обработке вручную, для мутантов 0408 и 0606, а для 0608 – выравнивание с большим весом. Water выдаёт такие же результаты, но в 0608 он отсекает первые 6 АО, поскольку нацелен на поиск оптимальных выравниваний вне зависимости от того, локальны они или глобальны. Небольшие разницы в цифрах можно объяснить разными критериями сходства АО.
| Алгоритм | Вер-ть мутации | Вер-ть замены | Иден-ть | Сходство | Вес | Выравнивание (сверху оригинальная посл-ть) |
| Needleman-Wunsch | 60% | 60% | 61.9% | 76.2% | 52.5 |
1 ADFDSSTCFH--LAEYRIPYQ 19
|
| 40% | 80% | 66.7% | 71.4% | 53.0 |
1 MP-AYNSNYTPTTRGMGQIVE 20
|
|
| 60% | 80% | 55.0% | 65.0% | 45.0 |
1 SAN-CRLFSLTEAVDFAEKW 19
|
|
| Smith-Waterman | 60% | 60% | 61.9% | 76.2% | 52.5 |
1 ADFDSSTCFH--LAEYRIPYQ 19
|
| 40% | 80% | 66.7% | 71.4% | 53.0 |
1 MP-AYNSNYTPTTRGMGQIVE 20
|
|
| 60% | 80% | 60.0% | 73.3% | 47.0 |
6 RLFSLTEAVDFAEKW 20
|
|
| Вручную | 60% | 60% | 61.90% | 66.67% | 52.5 |
174 ADFDSSTCFH--LAEYRIPYQ 193
|
| 40% | 80% | 66.67% | 76.20% | 54.0 |
97 MP-AYNSNYTPTTRGMGQIVE 116
|
|
| 60% | 80% | 45.00% | 55.00% | 43.0 |
242 GSANCRLFSLTEAVDFAEKW 261
|
Кратко об алгоритмах
Сам алгоритм можно поделить на две части: определение максимального веса вместе с последним элементом выравнивания и собственно выстраивание этого выравнивания. Для этих целей выстраивается матрица, во главе строк и столбцов которых стоят последовательности. На конкретном примере это будет, наверно, понятней.
Пусть мы имеем две последовательности нуклеотидов AATCG и ACGTCG. Cоставим нужные матрицы и обозначим некоторые условия:
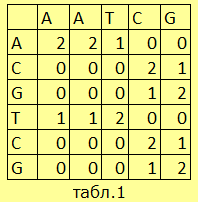 |
Идентичность нуклеотидов имеет вес (+2), совпадение комплементарных нуклеотидов – (+1), некомплементарных – 0, гэп – (-1). Составим матрицу, где в каждой клетке стоит вес его, так сказать, координат (cм.табл.1). |
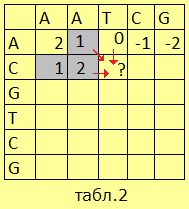 |
Теперь построим вторую матрицу, глядя на первую. Но теперь в каждой клетке будет стоять максимальный вес, который можно набрать на пути к ней, двигаясь из верхнего левого угла. В самую первую клетку можно попасть только одним способом, то есть запишем в неё её собственный вес-- (+2). Из неё мы можем перейти в три другие клетки, причём при переходе в две из них теряется по единице веса, поскольку, как несложно заметить, сейчас мы выполняем первую часть алгоритма, а последовательность координат клеток, в которые мы перемещаемся, однозначно задаёт выравнивание. |
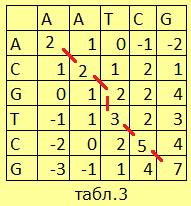 |
Таким образом заполним всю таблицу и обнаружим, что в нижнем правом углу образовалась (7), что больше любого другого числа. Можно
приступать ко второму шагу. Теперь мы идём по обратному пути: (7) могла получиться при переходе из одной из трёх окружающих клеток,
причём самое большое значение – в расположенной по диагонали. Значит, предпоследней клеткой являлась та, где стоит (5). |
AA-TCG
ACGTCGСтоит отметить, что в использованном для предыдущего задания мутанте 0608 программа Water отсекла первые 6 АО, так как в данном случае глобальное выравнивание не являлось оптимальным, как в двух остальных случаях.
К менее принципиальным отличиям можно отнести то, что Needle справляется со своей задачей и без применения штрафа за гэп, когда для Water это обязательное условие; зато Needle не оперирует отрицательными значениями веса сопоставлений, в отличие от Water.
Разницу между этими двумя алгоритмами и их альтернативное описание можно прочитать здесь.
А вот на этом видео вы можете просмотреть полноценную лекцию о динамическом программировании в биоинформатике.