Учебный сайт Фроловой Анастасии
Семестр 7. Биоинформатика в 3D.
На отрезке [0,30] ангстрем расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1,5 ангстрем друг от друга, молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего от 5 до 7 атомов (2+3 или 2+3+2). Электронные плотности атомов описываются гаусовой кривой. Максимум электронной плотности в центре атома приблизительно пропорционален числу электронов в атоме.
Функция на интервале [0,30] имеет вид нескольких гауссовых кривых в разных точках. Функция была создана с помощью скрипта compile-func.py. Гауссова функция определяется числами lambda,beta,gamma по формуле: gauss = lambda*exp(-(beta^2)*(X-gamma)^2). Параметры скрипта:
python compile-func.py -g 10,2,5+10,2,7+30.0,2,12+30.0,2,16+30.0,2,22+30,2,24.
Результатом этого скрипта является файл func.txt.
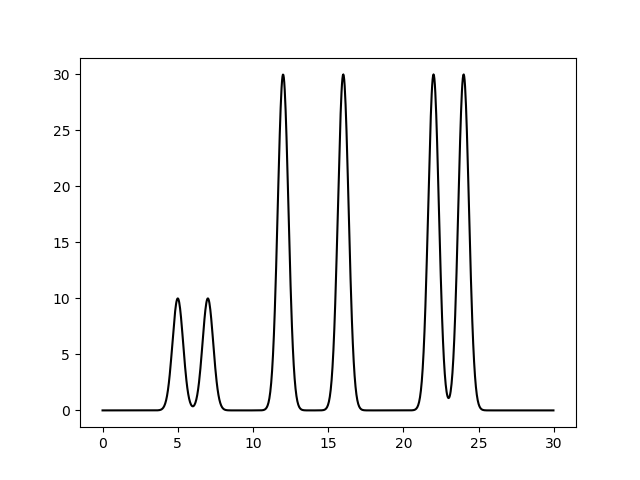
Рисунок 1. Электронная плотность полученной модели.
Максимумы четырех гауссовых функций в точках 5, 7, 12, 16, 22, 24, высоты в точках 10, 10, 30, 30, 30, 30 соответственно.
Амплитуды и фазы рассчитываются по выходной функции ЭП из скрипта compile-func.py. Выходная функция представлена выше.При моделировании экспериментальных данных учитывается то, что в эксперименте определяются амплитуды не для всех сигналов, интенсивности сигналов(а следовательно, и амплитуды) определяются с ошибкой, а также то, что фазы определяются для всех измененных сигналов, но тоже с ошибкой.
Коэффициенты Фурье рассчитываются с помощью скрипта func2fourier.py. Параметры скрипта:
python func2fourier.py -i func.txt -o func_ft.txt.
По умолчанию результаты записываются в файл func_ft.txt. В нем первый столбец соответствует номеру гармоники, второй - амплитуда (P), третий - фазе (phi). Общее количество гармоник равно 498, именно такое количество необходимо для восстановление полной функции.
Отбор гармоник был сделан при помощи скрипта fourier-filter.py. Параметры скрипта для отбора гармоник с 0 по 10: python fourier-filter.py -i func_ft.txt -r 0-10 -o func_ft_0_10.txt. По умолчанию выдает файл func_ft_filtered.txt.
Восстановить функцию по отобранным гармоникам можно скриптом fourier2func.py. Параметры скрипта для восстановления функции по первым 10 гармоникам, например:
python fourier2func.py -f func.txt -i func_ft_0_10.txt -o 0_10_func.txt.
Для полных наборов гармоник, когда известны все гармоники с номерами 0,1,2,..,n, я восстановила функции ЭП по разному количеству гармоник от 0 до 10, 15, 20, 25, 30. Полученные результаты представлены на рисунках 2 и 3.
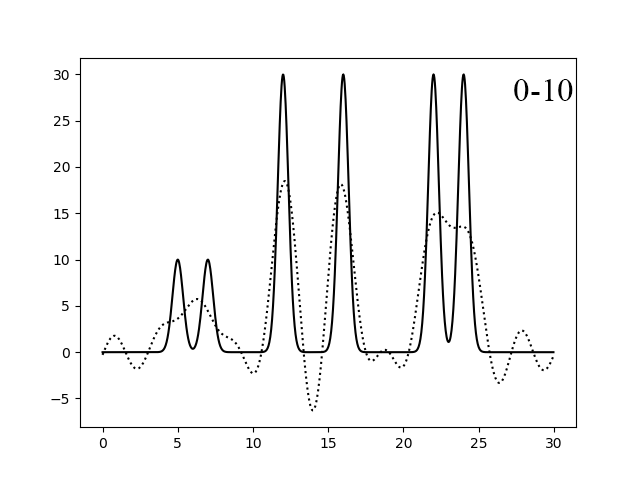

Рисунок 2. Восстановление функции по первым 10 (левый) и 15 (правый) гармоникам.
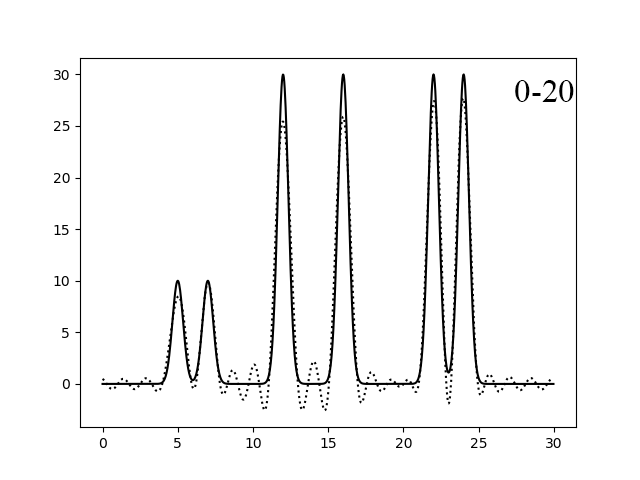
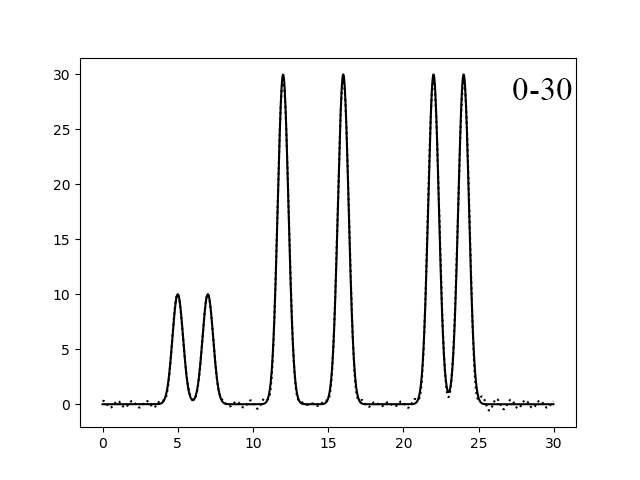
Рисунок 3. Восстановление функции по первым 20 (левый) и 30 (правый) гармоникам.
Как видно из рисунков 2-3, если брать гармоники с 0-10 и 0-20, то функция восстанавливается более менее хорошо. А при гармониках от 0 до 20 и 30, восстановление отличное.
При восстановлении функции я так же добавляла 10%, 30% и 50% шума к амплитудам и фазам отдельно (рисунки 4-7).
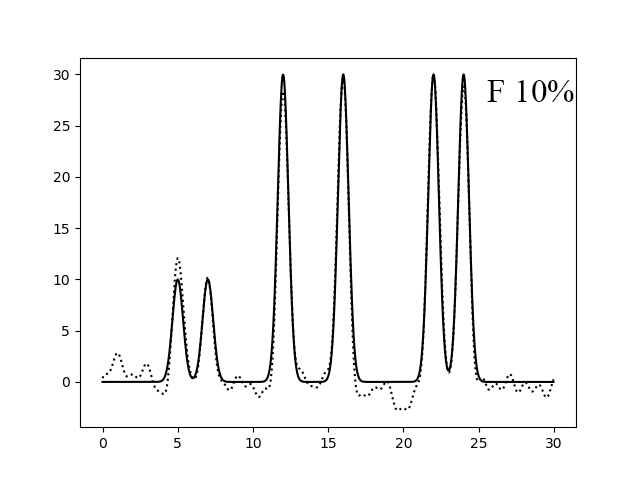
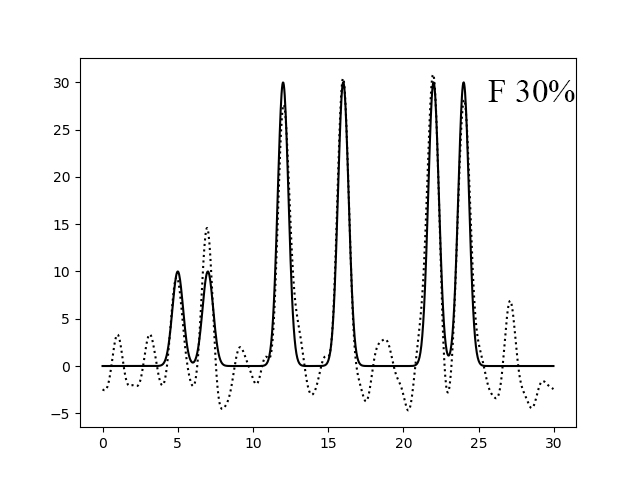
Рисунок 4. Восстановление функции по первым 30 гармоникам с добавлением 10% (левый) и 30% (правый) шума к амплитудам.
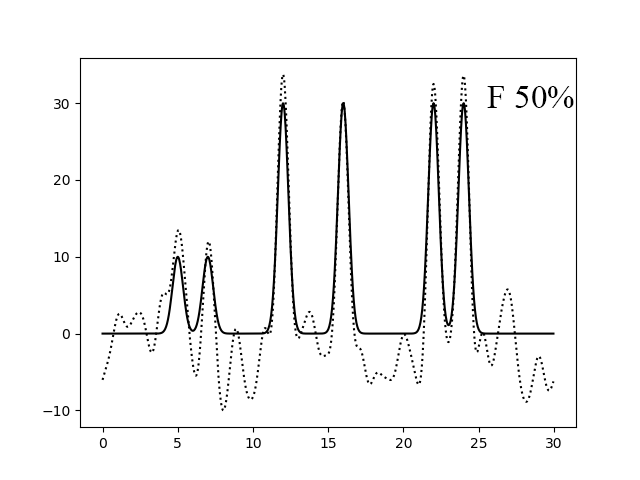
Рисунок 5. Восстановление функции по первым 30 гармоникам с добавлением 50% шума к амплитудам.
Добавление шума к амплитудам не так сильно влияет на качество восстановления, так как мы можем определить максимумы функции (рисунки 4-5). Однако, если добавить шум к фазам, то это оказывает сильное влияние на качество. При Р 50% (рисунок 7) уже невозможно определить максимумы нескольких атомов.
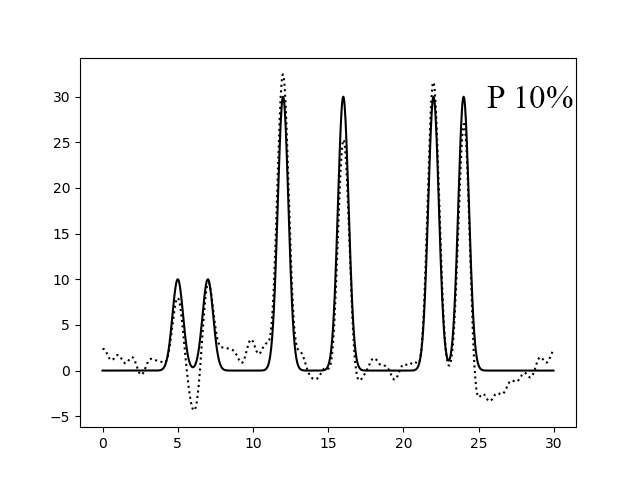
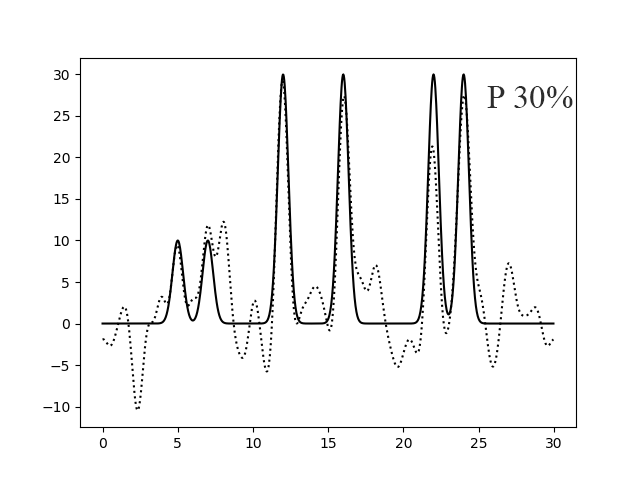
Рисунок 6. Восстановление функции по первым 30 гармоникам с добавлением 10% (левый) и 30% (правый) шума к фазам.
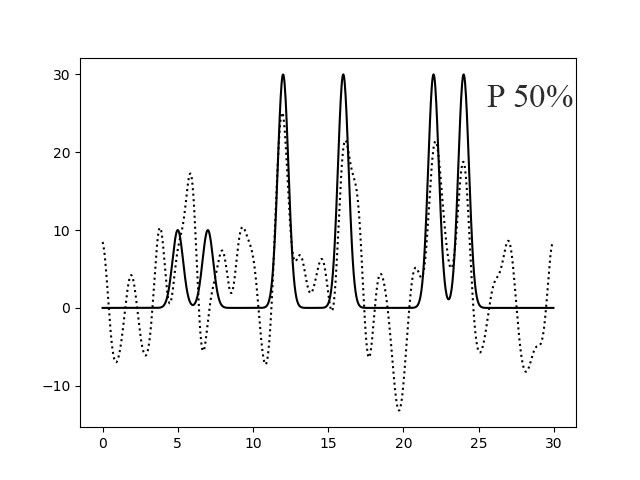
Рисунок 7. Восстановление функции по первым 30 гармоникам с добавлением 50% шума к фазам.
Так же я посмотрела как будет влиять 10% и 50% шума к амплитудам и фазам вместе (рисунок 8). И как видно, при 50% шума появляется очень много пиков и это сильно снижает уровень восстановления функции.
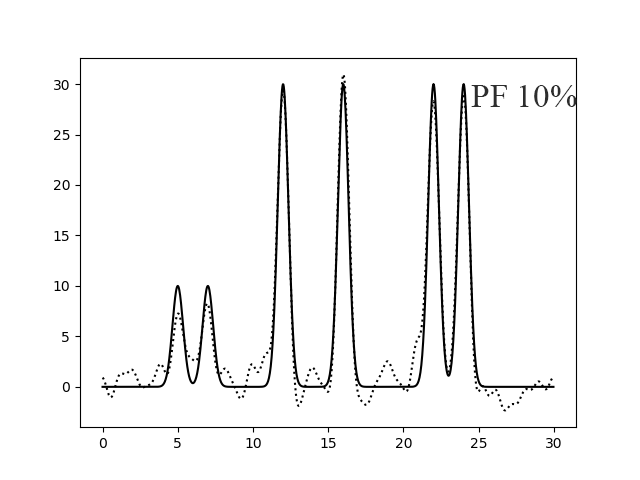
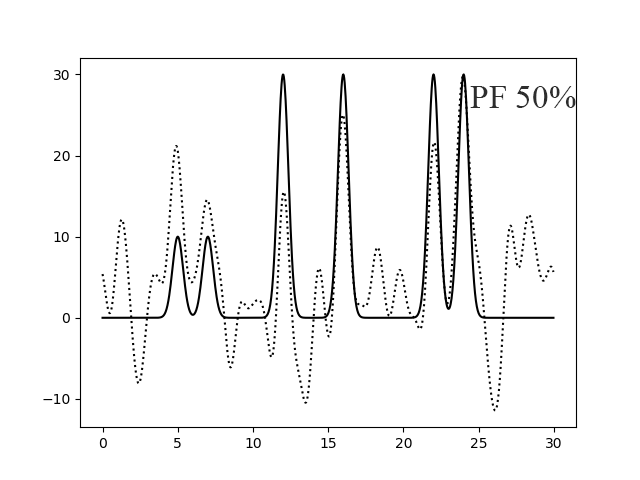
Рисунок 8. Восстановление функции по первым 30 гармоникам с добавлением 10 % (левый) и 50% (правый) шума к амплитудам и фазам вместе.
Кроме того, интересно посмотреть какой из шумов (к амплитуде или фазе) будет сильнее мешать восстановлению функции (рисунок 9). Они оба вносят сильный вклад в качество восстановления функции, но мне кажется, что шум к фазе оказывает большее влияние, чем к амплитуде.
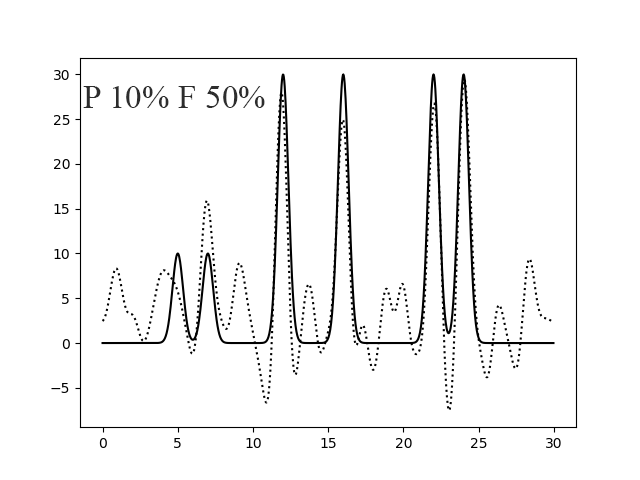
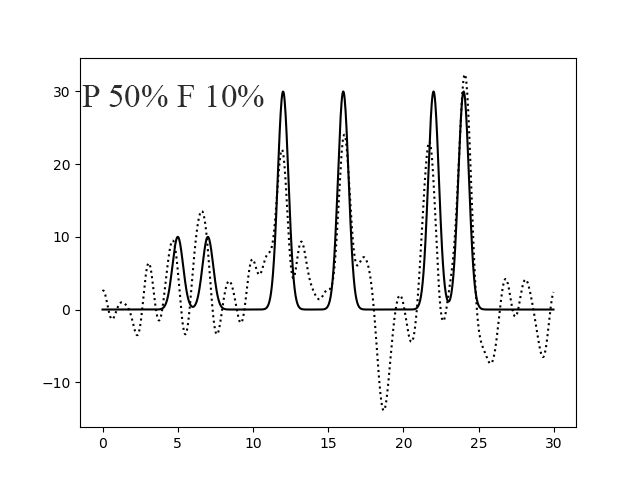
Рисунок 9. Восстановление функции по первым 30 гармоникам с добавлением 10% шума к амплитуде и 50% шума к фазе (левый) и наоборот (правый).
Из полных гармоник я сделала неполные, из которых удалила некоторые гармоники (например, первые или из середины). Результаты показаны на рисунках 10-12.
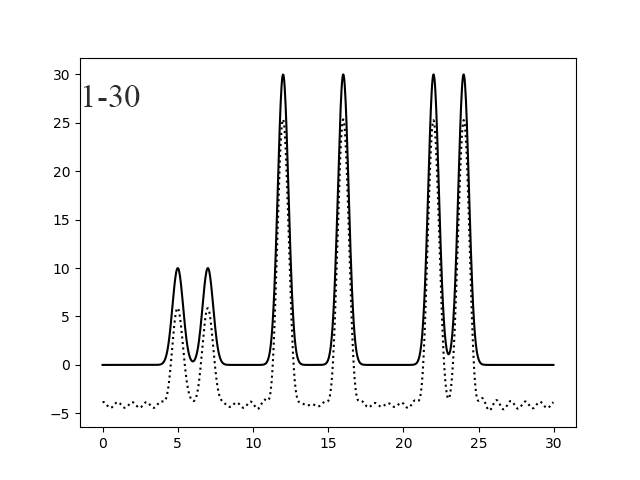
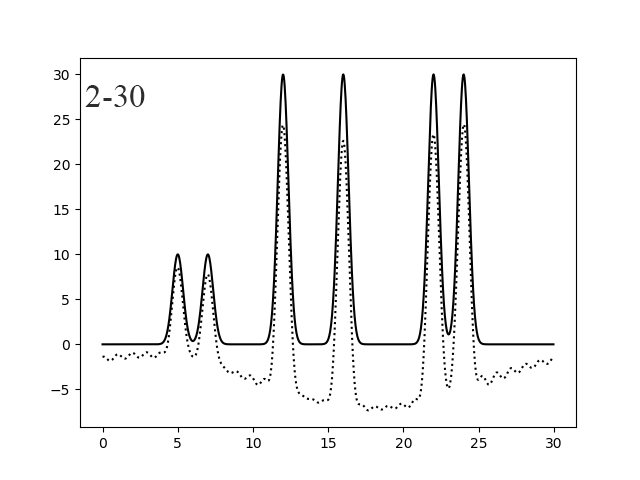
Рисунок 10. Восстановление функции по 1-30 (левый) и 2-30 (правый) гармоникам.
Удаление 0 гармоники приводит к понижению функции и на качестве восстановления не сказывается, а удаление 0 и 1 гармоник - к прогибу функции вниз.
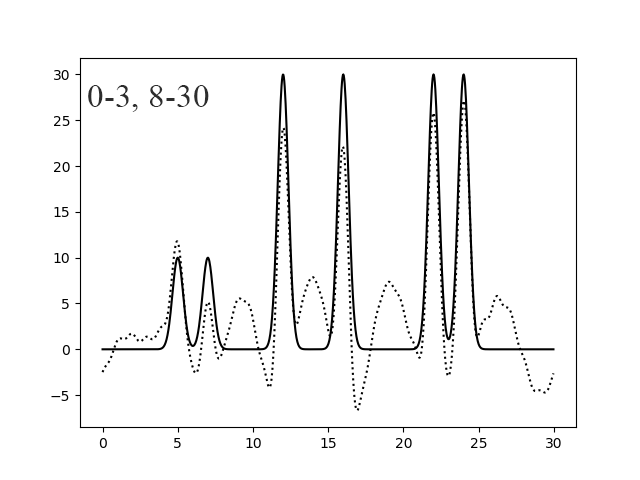
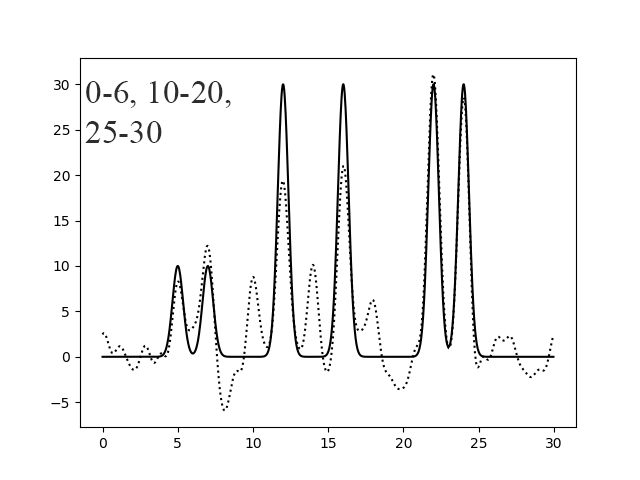
Рисунок 11. Восстановление функции по 0-3,8-30 (левый) и 0-6,10-20, 25-30 (правый) гармоникам.
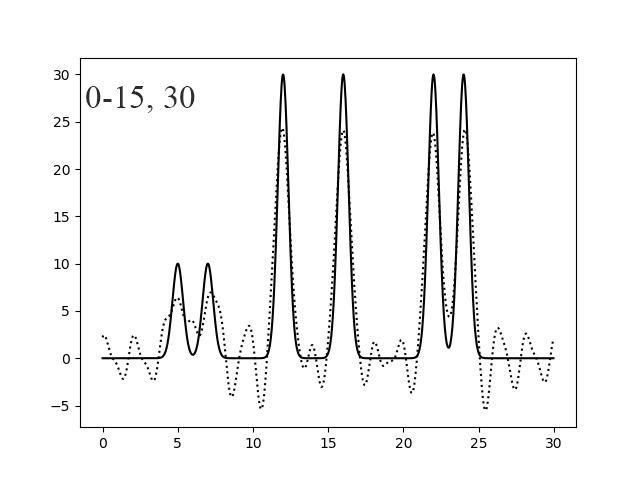
Рисунок 12. Восстановление функции по 0-15, 30 гармоникам.
Описание каждого графика занесено в таблицу. Качество восстановления описывается 4 вариантами: отличное (по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов")), хорошее (можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума), среднее (положение каких-то атомов определить по восстановленной функции нельзя, других - можно) и плохое (положение атомов определить не представляется возможным, можно только предсказать примерный размер "молекулы"). Все данные по восстановлению функций собраны в таблице 1.
Таблица 1. Восстановление функции по коэффициентам ряда Фурье (файл).
| Набор гармоник | Разрешение, Å | Полнота данных (%)) | Шум амплитуды (% от величины F) | Шум фазы (% от величины phi) | Качество восстановления (отличное, хорошее, среднее, плохое) | Комментарии |
| Полный набор гармоник | ||||||
| 0-10 | 3 | 100 | 0 | 0 | среднее | Можно четко определить максимумы двух слагаемых функции |
| 0-15 | 2 | 100 | 0 | 0 | хорошее | |
| 0-20 | 1,5 | 100 | 0 | 0 | отличное | |
| 0-30 | 1 | 100 | 0 | 0 | отличное | Восстановленная функция полностью совпадает с исходной |
| 0-30 | 1 | 100 | 10 | 0 | отлично | |
| 0-30 | 1 | 100 | 30 | 0 | отлично | |
| 0-30 | 1 | 100 | 50 | 0 | хорошо | Появляются небольшие пики, которые можно было бы принять за еще один атом (водород) |
| 0-30 | 1 | 100 | 0 | 10 | отлично | |
| 0-30 | 1 | 100 | 0 | 30 | среднее | |
| 0-30 | 1 | 100 | 0 | 50 | плохое | Очень много разных пиков |
| 0-30 | 1 | 100 | 10 | 10 | отличное | |
| 0-30 | 1 | 100 | 50 | 50 | плохое | |
| 0-30 | 1 | 100 | 10 | 50 | плохое | |
| 0-30 | 1 | 100 | 50 | 10 | плохое | |
| Неплоный набор гармоник | ||||||
| 1-30 | 1 | 96,7 | 0 | 0 | отличное | Высота пиков ниже |
| 2-30 | 1 | 93,5 | 0 | 0 | отличное | Высота пиков ниже и восстановленная функция прогибается вниз |
| 0-3, 8-30 | 1 | 87 | 0 | 0 | хорошее | |
| 0-6, 10-20, 25-30 | 1 | 77,4 | 0 | 0 | хорошее | |
| 0-15,30 | 1 | 54,83 | 0 | 0 | среднее | |