Разложение функции в ряд Фурье

В этом практикуме было проанализировано качество восстановления одномерной функции электронной плотности в зависимости от полноты набора измеренных гармоник и величины экспериментального шума.
Для начала была смоделирована функция электронной плотности в одномерной элементарной ячейке на отрезке [0,30]. Модель представляла собой две молекулы, расположенные на расстоянии около 5 Å друг от друга. Первая молекула состояла из двух атомов, вторая - из трех.
Функция была получена с помощью скрипта compile-func.py (этот скрипт использует дополнительный модуль fourier) с параметрами 37,3,5 + 28,3,6.4 + 19,3,10.5 + 32,3,11.9 + 14,3,13.3 (сумма пяти гауссовских функций с максимумами в точках 5, 6.4, 10.5, 11.9, 13.3 и с величиной пиков 37, 28, 19, 32, 14).
График полученной функции представлен на рисунке 1.

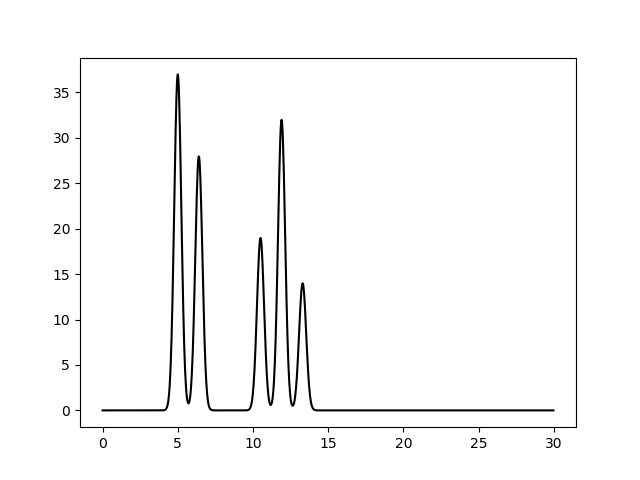
Рисунок 1. Функция электронной плотности для одномерного случая, смоделированная для системы из двух молекул, состоящих из 2 и 3 атомов.

Далее функция была разложена в ряд Фурье с помощью скрипта func2fourier.py. Полученный файл содержал 499 гармоник, которые в сумме дают исходную функцию.
Затем было подобрано такое количество гармоник (с первой по N), по которым можно было с достаточной точностью восстановить исходную функцию. Для восстановления функции электронной плотности по набору гармоник был использован скрипт fourier2func.py, а для отбора необходимых гармоник из полного набора - скрипт fourier-filter.py.
На рисунке 2 показаны графики функций электронной плотности, восстановленные по первым 10, 15, 20, 25, 30 и 50 гармоникам разложения.

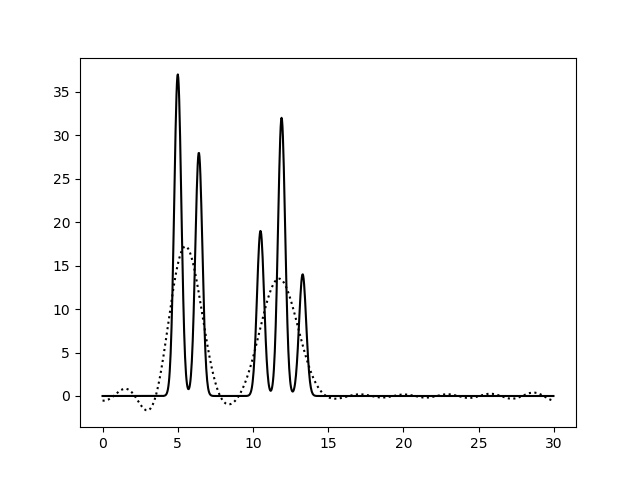
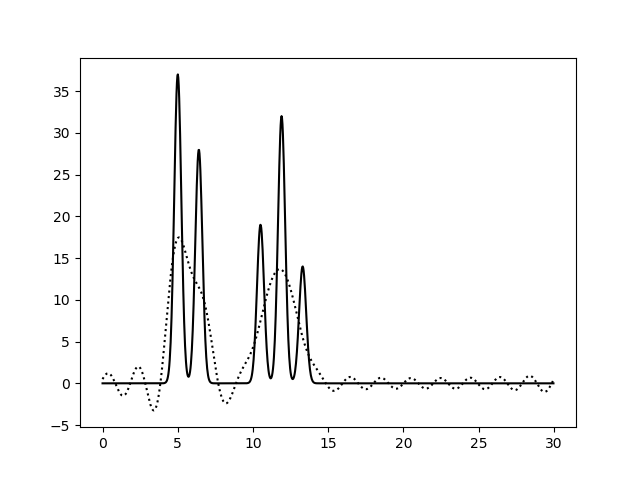
Рисунок 2a. Функция электронной плотности, восстановленная по первым 10 (слева) или 15 (справа) гармоникам.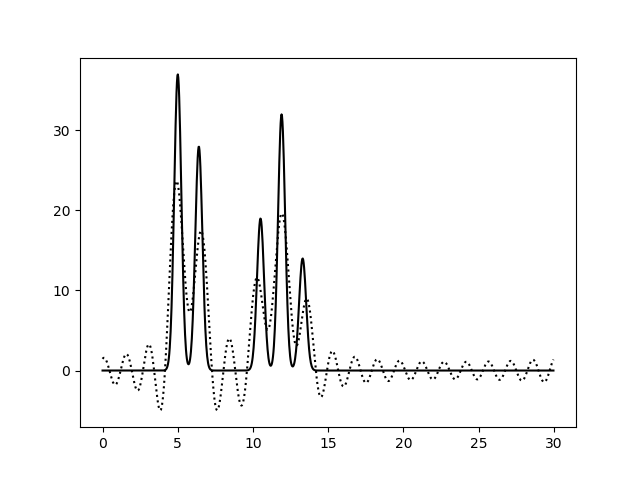

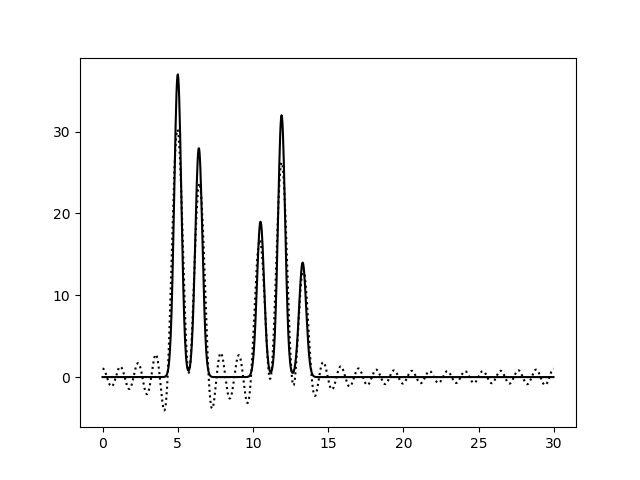
Рисунок 2b. Функция электронной плотности, восстановленная по первым 20 (слева) или 25 (справа) гармоникам.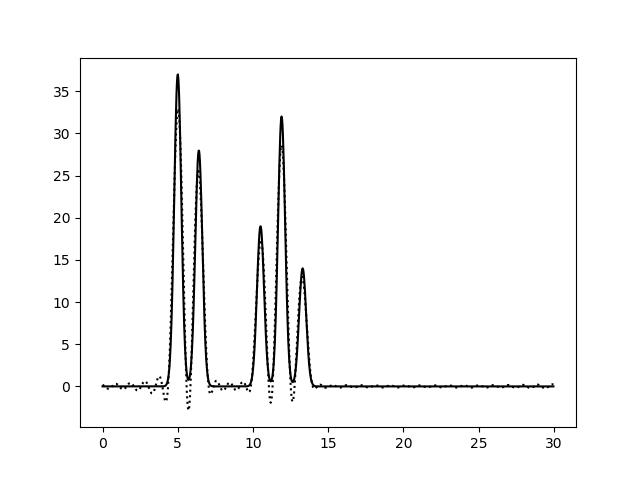

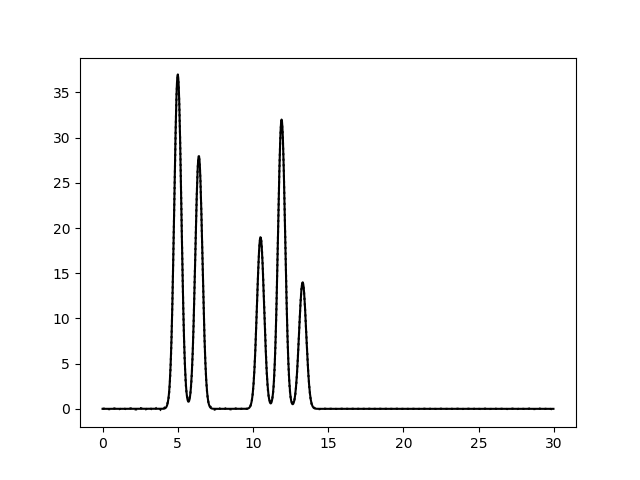
Рисунок 2c. Функция электронной плотности, восстановленная по первым 30 (слева) или 50 (справа) гармоникам.

По первым 10 гармоникам можно определить только общие размеры молекул и их примерное положение, расположение отдельных атомов определить невозможно (плохое качество восстановления). Далее, по 20 гармоникам, уже можно определить положение отдельных атомов, хотя и немного неточно, однако значения максимумов функции ниже исходных, а некоторые пики от шума можно принять за дополнительные атомы (хорошее восстановление). При восстановлении по первым 30 гармоникам положения атомов уже устанавливаются точно и однозначно, высота пиков почти соотвествует исходным значениям, а уровень шума очень низок (отличное восстановление). За N было принято значение 30. Далее вся работа проводилась с набором гармоник 0-30.

Затем было изучено влияние добавления шума (к фазам и/или к амплитудам) на восстановление функции электронной плотности. На рисунке 3 представлены графики электронной плотности, восстановленные по первым 30 гармоникам ряда Фурье с добавлением шума к амплитудам (10, 20 и 40), к фазам (10, 20 и 40) и одновременно к обоим параметрам (10/10, 30/30, 20/40 и 40/20).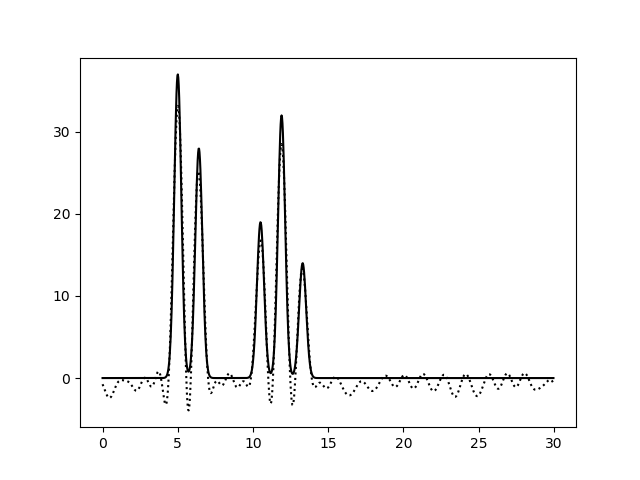

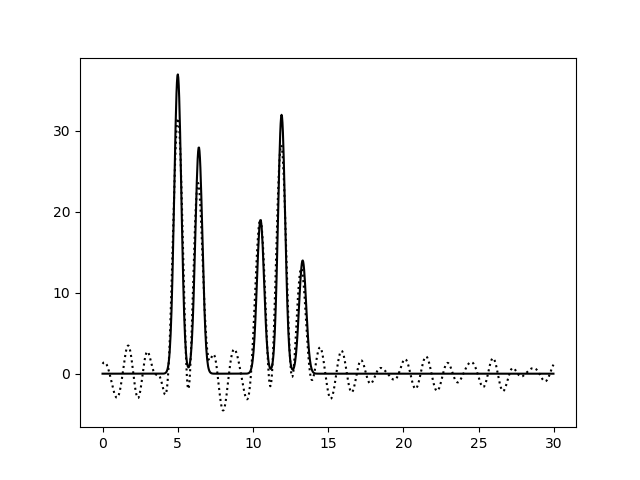
Рисунок 3a. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 10% шума к амплитудам (слева) или к фазам (справа).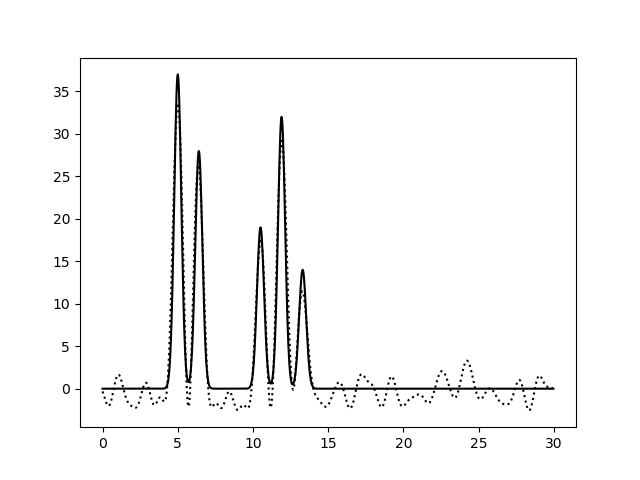

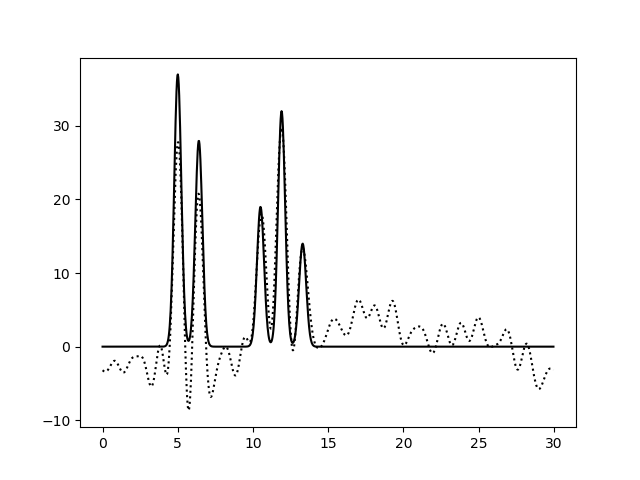
Рисунок 3b. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к амплитудам (слева) или к фазам (справа).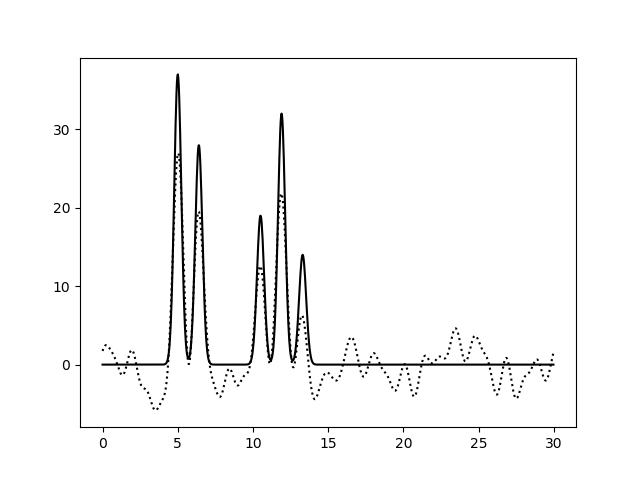

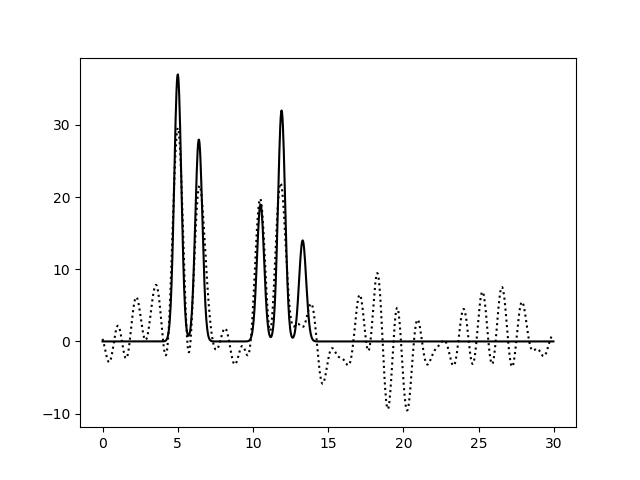
Рисунок 3c. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 40% шума к амплитудам (слева) или к фазам (справа).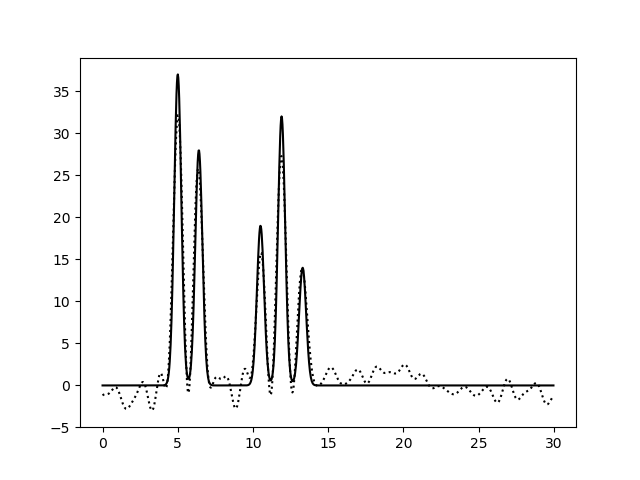

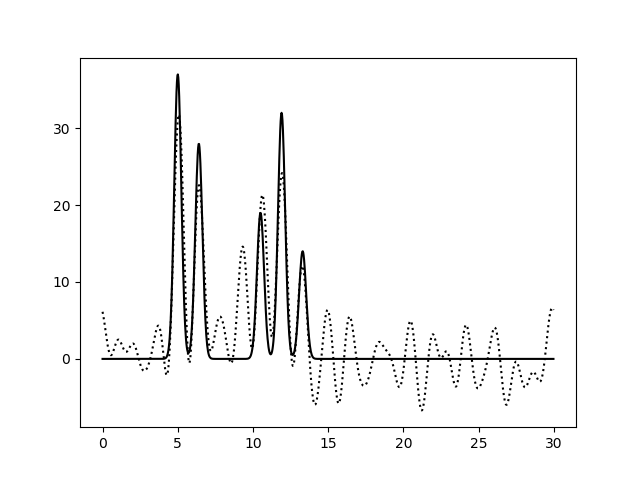
Рисунок 3d. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением к амплитудам и к фазам 10% (слева) или 30% (справа) шума.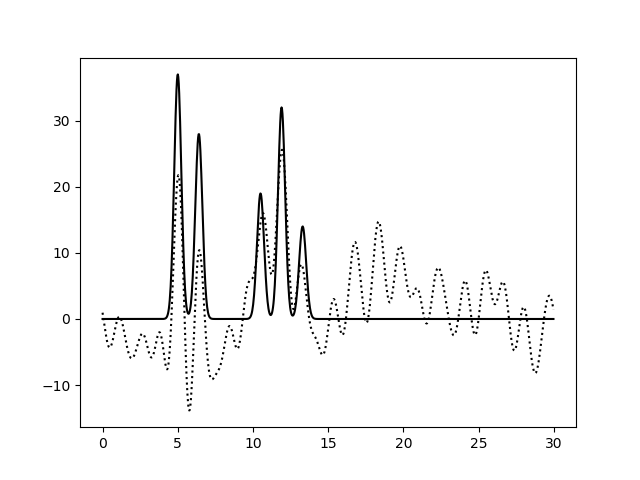

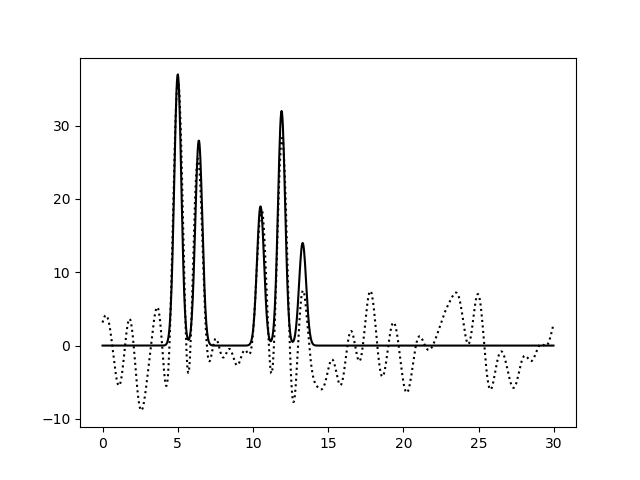
Рисунок 3e. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к амплитудам и 40% шума к фазам (слева) или 40% шума к амплитудам и 20% шума к фазам (справа).

По рисунку 3 можно заметить, что увеличение степени шума по амплитудам не приводит к существенным изменениям вида функции электронной плотности: положения пиков определяются достаточно точно, а уровень шума низок и не позволяет определить лишние атомы (рисунки 3a, 3b, 3c слева). Однако увеличение степени шума по фазам уже на уровне 20% приводит к небольшому сдвигу координат атомов и к сильному увеличению уровня шума (рисунки 3a, 3b, 3c справа).
Если добавить шум одновременно к фазам и амплитудам, то при низком уровне шума (10%) это практически не сказывается на функции электронной плотности, однако при уровне шума 30% уже нельзя точно определить положения атомов, а также появляется много лишних пиков (рисунок 3d). Чтобы узнать, какой из параметров (фазы или амплитуды) в этом случае больше влияет на искажение функции элеткронной плотности, были построены графики с уровнем шума 20% по одному из параметров и одновременно 40% - по другому. По рисунку 3e можно заключить, что добавление шума к фазам приводит к более серьезным искажениям в восстановленной функции.

Наконец, было проанализировано, как восстанавливается функция электронной плотности по неполному набору гармоник. В реальном эксперименте редко удается измерить все гармоники, поэтому такой анализ будет соответствовать работе с экспериментальными данными.
Функции электронной плотности для всех проанализированных случаев представлены на рисунке 4.
При восстановлении по всем гармоникам набора, кроме первой (1-30), функция электронной плотности практически не отличается от исходной (с точностью до положения атомов и примерной высоты пиков). Если не удалось измерить первые две гармоники (2-30), положения атомов все равно удается определить достаточно точно (рисунок 4a).
При удалении нескольких гармоник из середины набора (подряд или нет) положения атомов также хорошо различимы, однако во втором случае наблюдается достаточно высокий уровень шума (рисунок 4b).
Если добавить еще одну грамонику (номер 40), то функция восстанавливается достаточно точно (рисунок 4c, слева). В том случае, если функция восстанавливалась по набору гармоник 0-20,40, пики немного смещены относительно их истинного положения, уровень шума относительно высокий, а некоторые пики немного перекрываются. Можно заметить, что добавление гармоники 40 не улучшает восстановление по сравнению с набором 0-20 (рисунок 2b, слева).

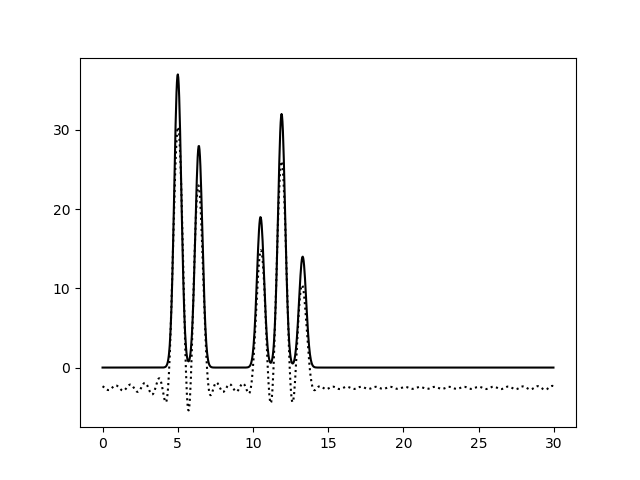
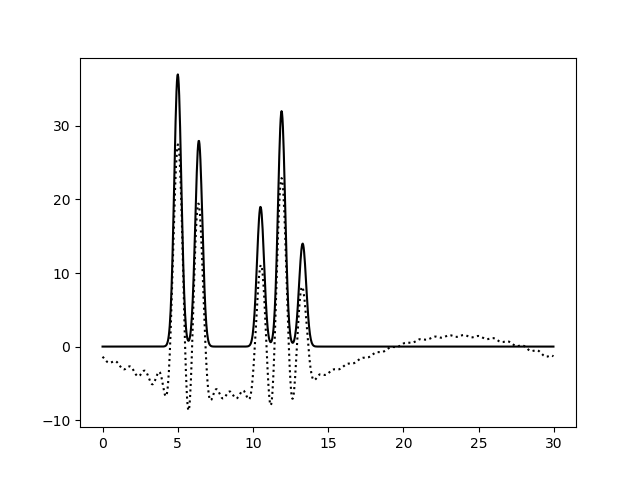
Рисунок 4a. Функция электронной плотности, восстановленная по наборам гармоник 1-30 (слева) или 2-30 (справа).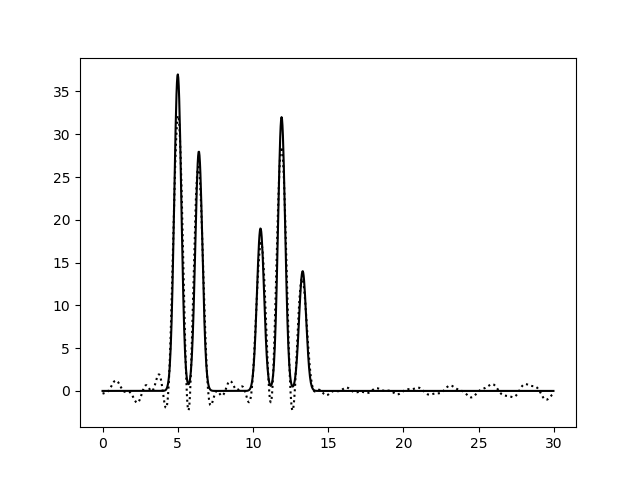

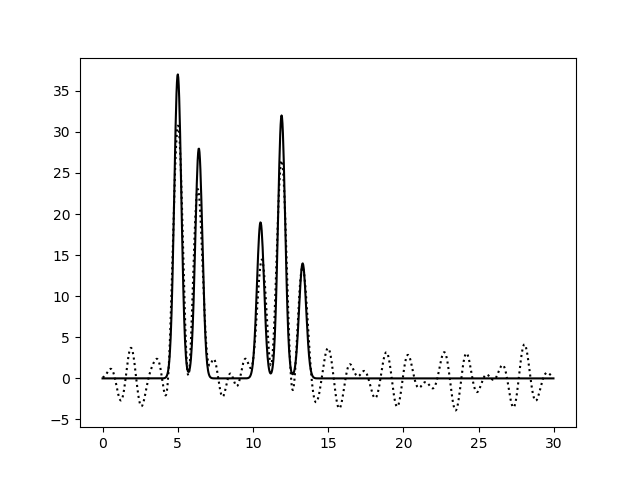
Рисунок 4b. Функция электронной плотности, восстановленная по наборам гармоник 0-10,13-30 (слева) или 0-10,12-15,17-22,24-30 (справа).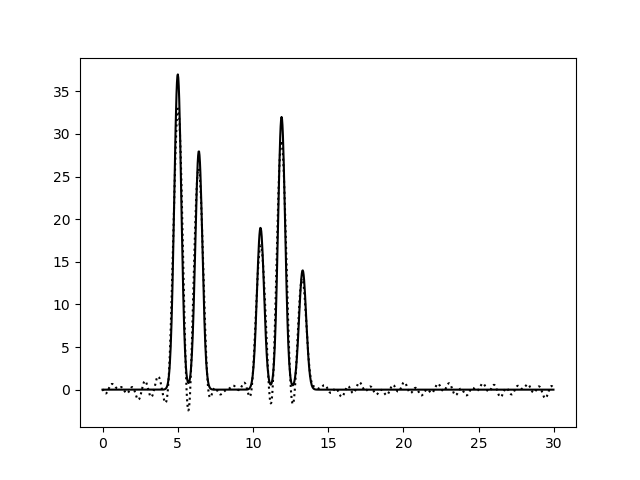

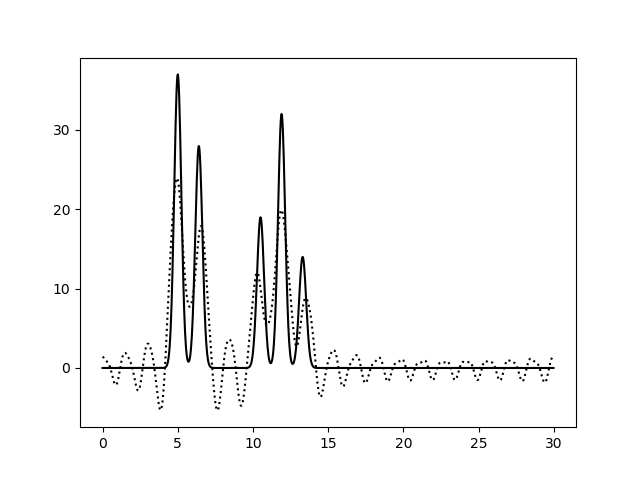
Рисунок 4c. Функция электронной плотности, восстановленная по наборам гармоник 0-10,12-30,40 (слева) или 0-20,40 (справа).

В таблице 1 представленна суммарная информация об исследованных наборах гармоник и о качестве восстановления функции электронной плотности по этим наборам.

© Наталия Кашко, 2017