Модель для компьютерного эксперимента. На отрезке [0,30] (ангстремы) расположены две молекулы. Атомы в молекуле связаны ковалентно и находятся на расстоянии 1-1.5 анстрем друг от друга. Молекулы расположены на расстоянии 3-5 ангстрем (водородная связь или гидрофобное взаимодействие между ними). Всего 5 атомов (3+2). Электронные плотности (ЭП) атомов описываются гауссовой кривой. Максимум ЭП в центре атома приблизительно пропорционален числу электронов в атоме. Использовались разные атомы.
Командой:
python compile-func.py -g 36,3,4.5+25,3,6.1+11,3,7.5+31,3,11.5+12,3,13.5
была получена функция с параметрами -g, у которой есть 6 слагаемых, каждое из которых
описывает атом. Каждое слагаемое состоит из 3-ех чисел: первое - высота пика (число
электронов), второе - ширина пика (размер атома) и третье - положение пика на прямой (1D-
пространство, в котором происходит генерация ЭП). Функция показана на Рис. 1.
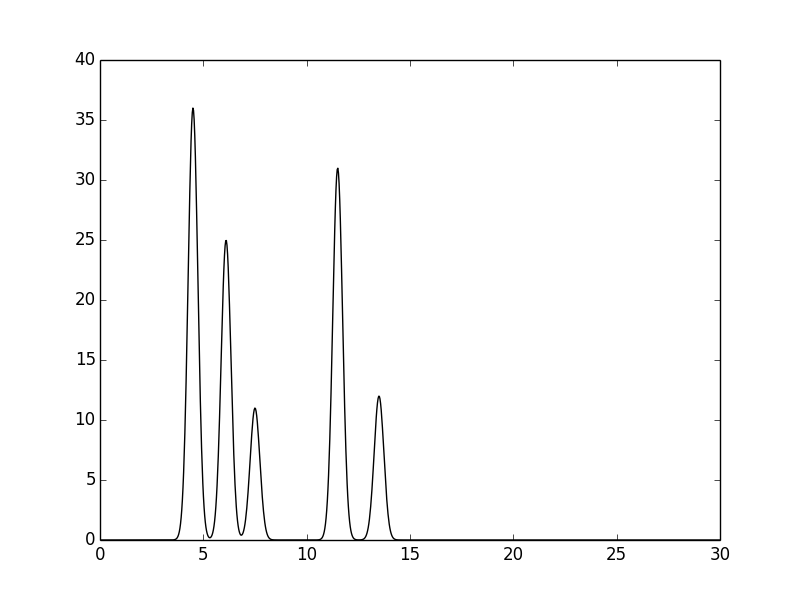
Рис. 1. Функция электронной плотности для одномерного случая, смоделированная для системы из двух молекул, состоящих из 3 и 2 атомов.
Расчет амплитуд и фаз сигналов, моделирующих экспериментальные данные
Командой:
python func2fourier.py -i func.txt
были получены коэффициенты Фурье.
Из 499 гармоник, то есть, по полному набору, нашли n_0, при котором восстановление отличное.
Командами:
python fourier-filter.py -i func_ft.txt -r 0-10 -o func_ft_0_10.txt
python fourier2func.py -f func.txt -i func_ft_0_10.txt -o 0_10_func.txt
получены функции, представленные на Рис. 2-6 (сплошной черной линией изображена
исходная функция, а пунктиром изображена функция по выбранным гармоникам). 0-10 - это необходимое число гармоник.
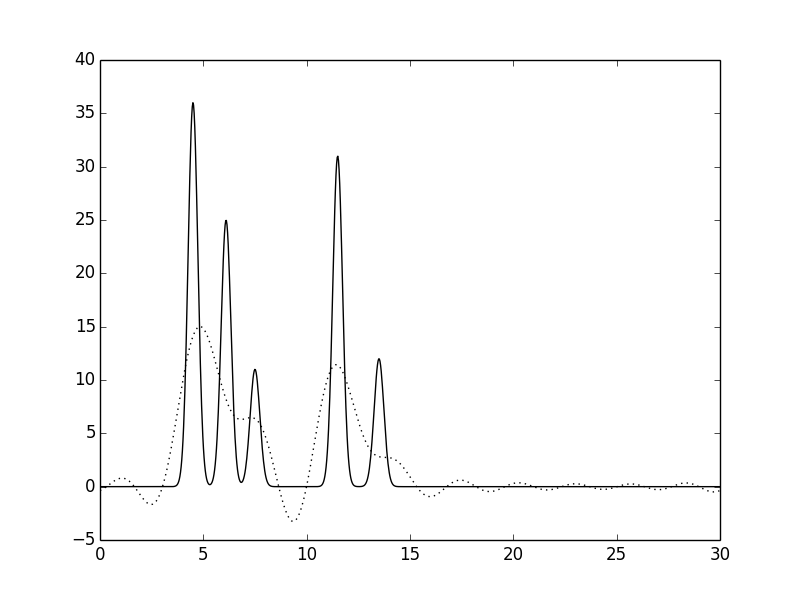
Рис. 2. Функция электронной плотности, восстановленная по первым 10 гармоникам.
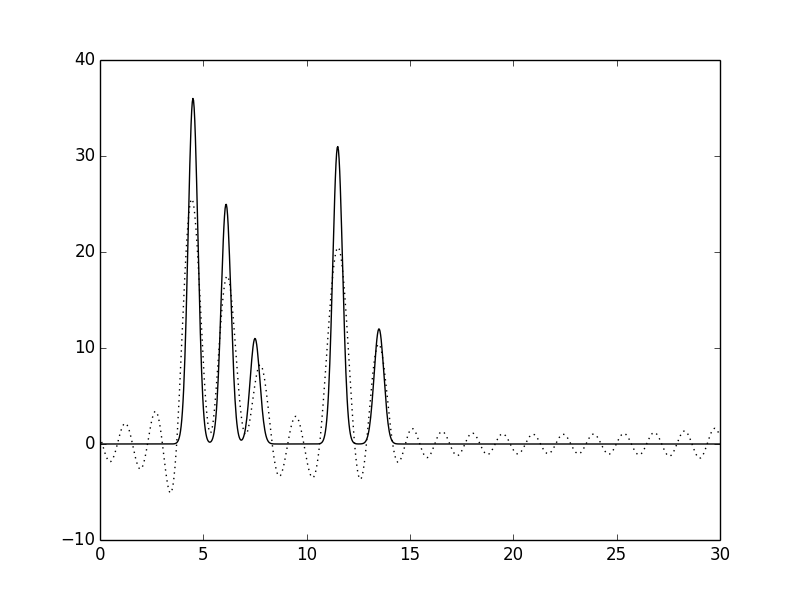
Рис. 3. Функция электронной плотности, восстановленная по первым 20 гармоникам.
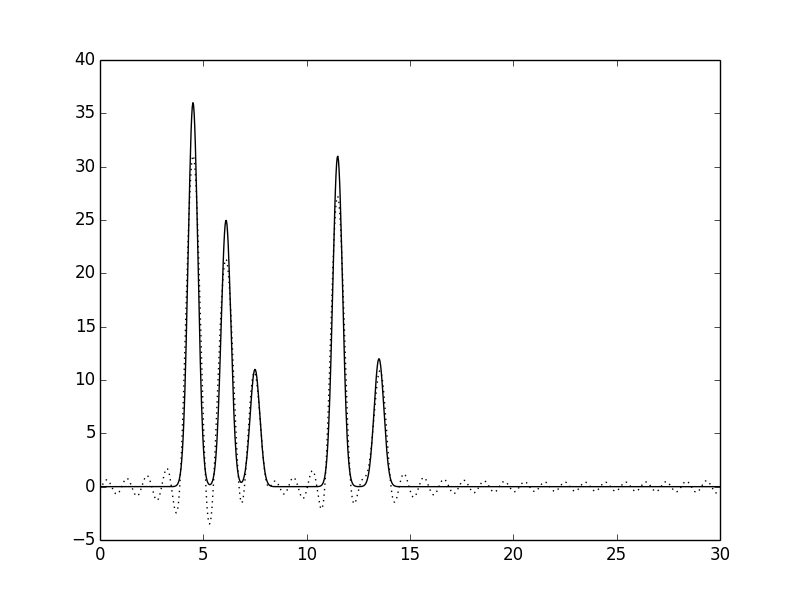
Рис. 4. Функция электронной плотности, восстановленная по первым 30 гармоникам.
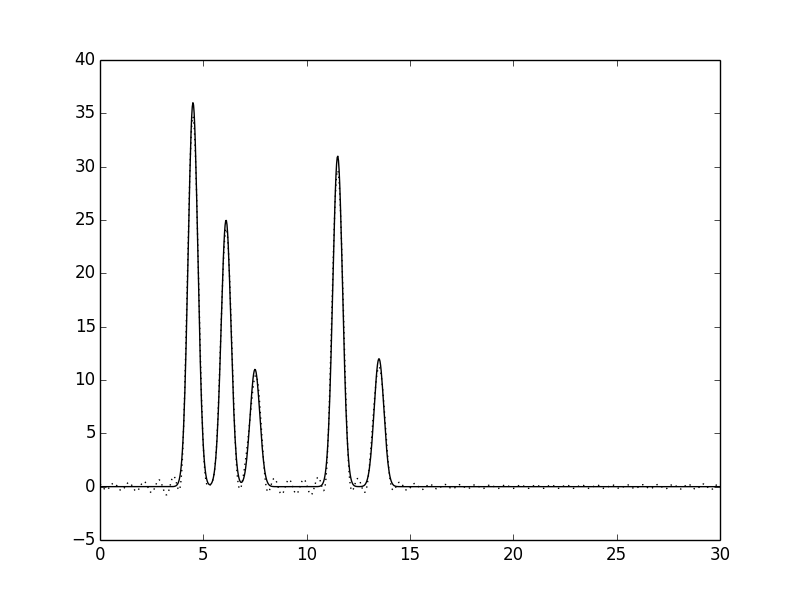
Рис. 5. Функция электронной плотности, восстановленная по первым 40 гармоникам.
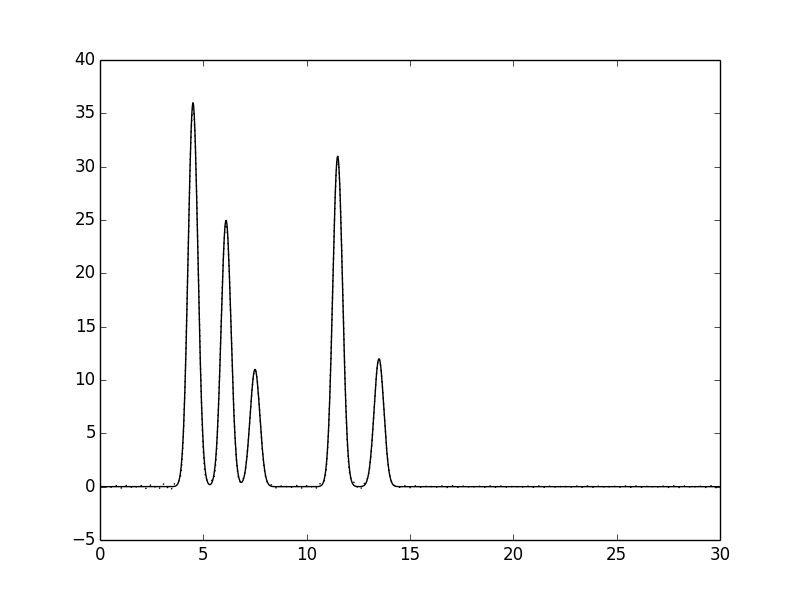
Рис. 6. Функция электронной плотности, восстановленная по первым 50 гармоникам.
По первым 10 гармоникам можно определить только общие размеры молекул и их примерное положение, расположение отдельных атомов определить невозможно (плохое восстановление). По первым 20 гармоникам можно определить положение отдельных атомов, но значения максимумов функции существенно ниже исходных, а некоторые пики от шума можно принять за дополнительные атомы (хорошее восстановление). По первым 30 гармоникам положения атомов устанавливаются точно и однозначно, высота пиков почти соотвествует исходным значениям, а уровень шума очень низок (отличное восстановление). За n_0 было принято значение 30. Далее вся работа проводилась с набором гармоник 0-30. Восстановление функции электронной плотности по модельным ("экспериментальным") данным с добавлением шума к амплитуде и фазе
В расчет коэффициентов Фурье был добавлен шум к амплитудам или фазам (параметры –F и –P скрипта func2fourier.py). Например, для F=20% и P=40% использовались следующие команды:
python func2fourier.py -F 20 -P 40 -i func.txt -o ft_noise20-40.txt
python fourier-filter.py -r 0-30 -i ft_noise20-40.txt -o ft_noise20-40_n0.txt
python fourier2func.py -i ft_noise20-40_n0.txt -o two_func_noise20-40_n0.txt
Результаты представлены на Рис. 7-17.
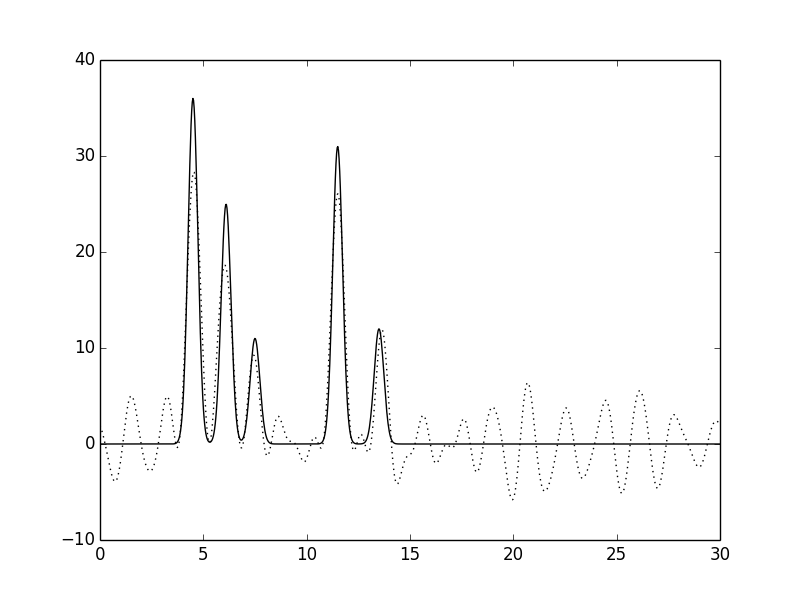
Рис. 7. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к фазам.
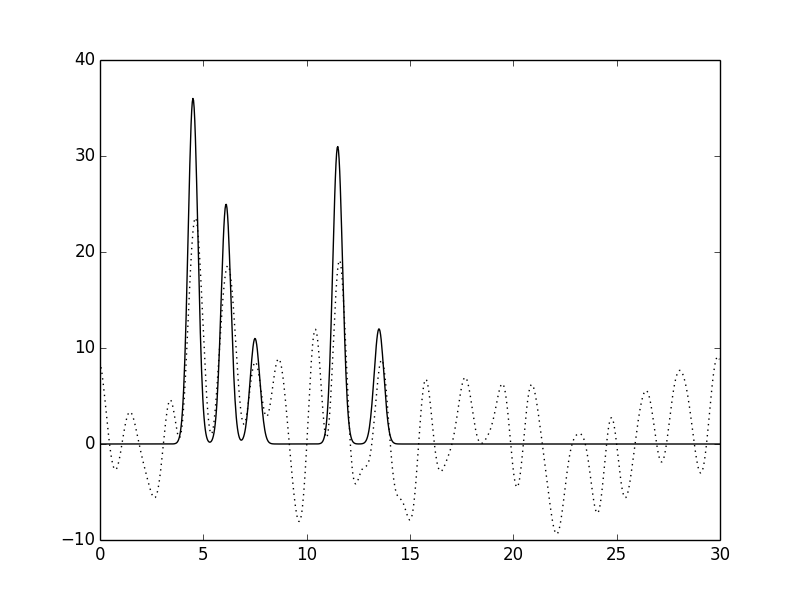
Рис. 8. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 40% шума к фазам.
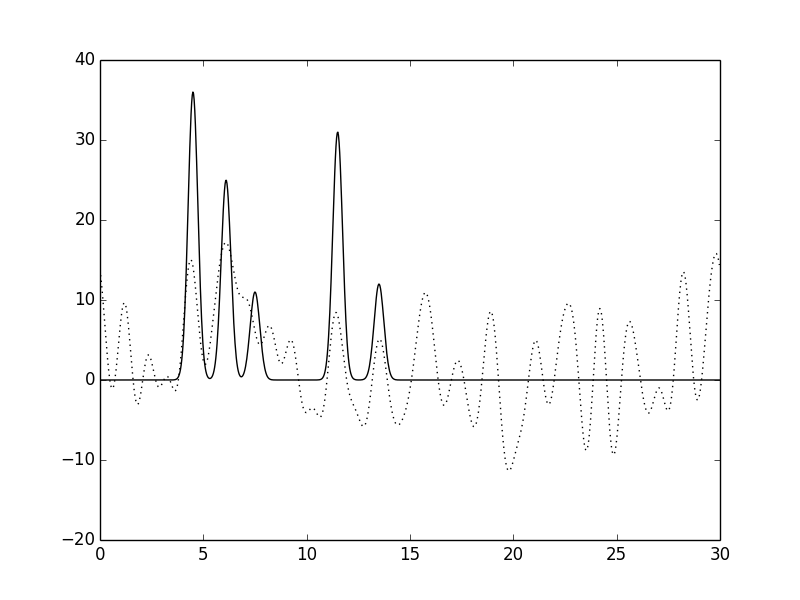
Рис. 9. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 60% шума к фазам.
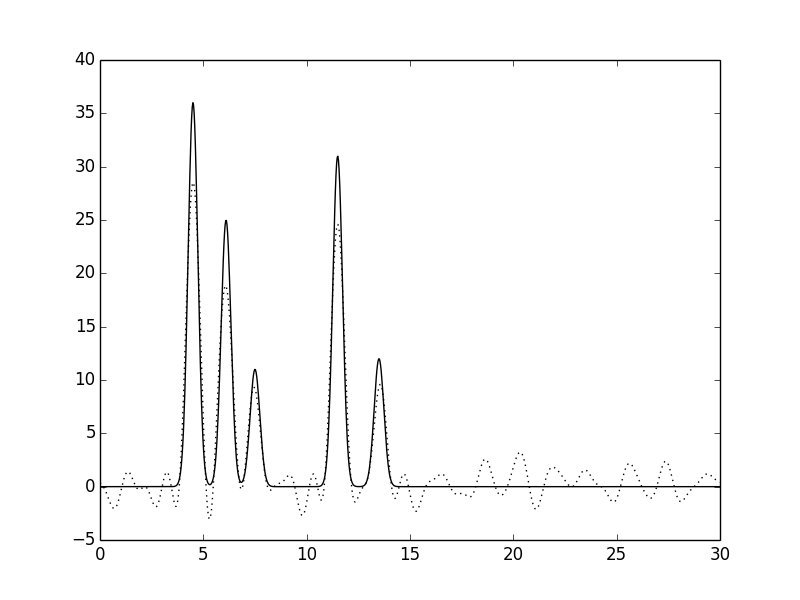
Рис. 10. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 20% шума к амплитудам.
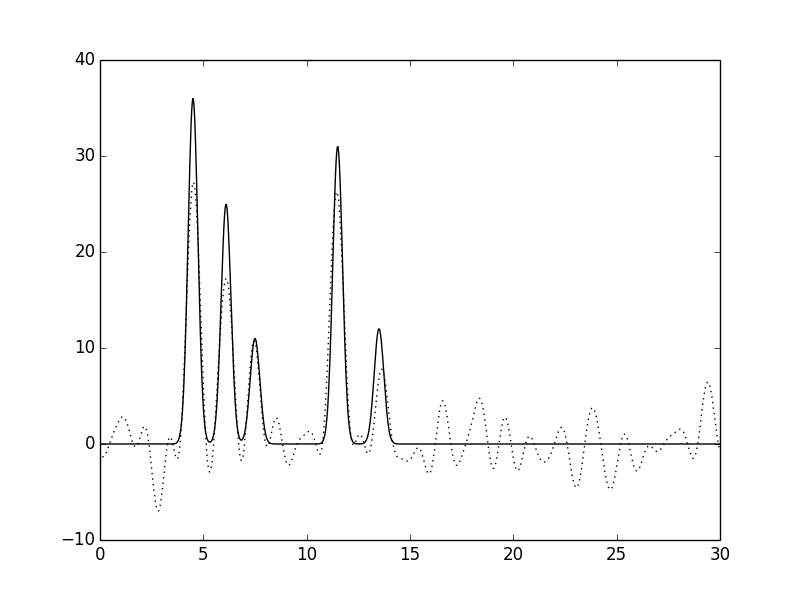
Рис. 11. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 40% шума к амплитудам.
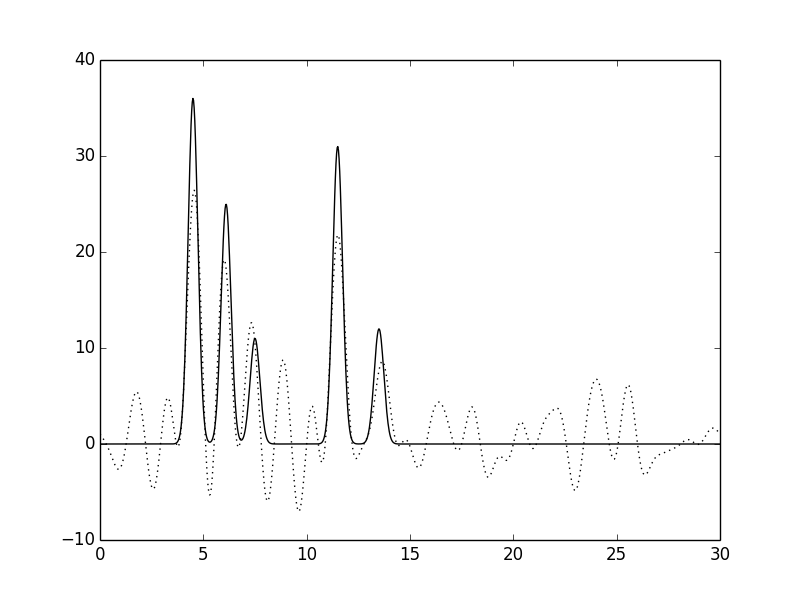
Рис. 12. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением 60% шума к амплитудам.
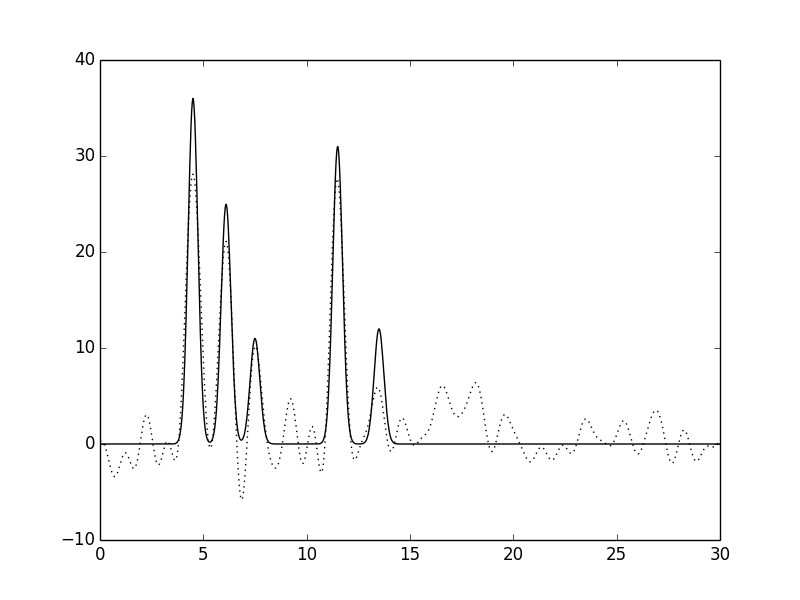
Рис. 13. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением к амплитудам и к фазам 20% шума.
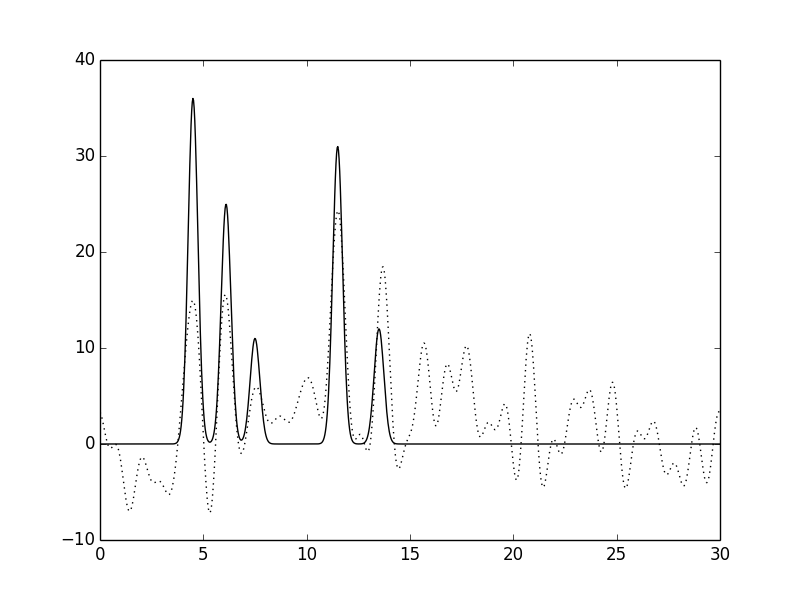
Рис. 14. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением к амплитудам и к фазам 40% шума.
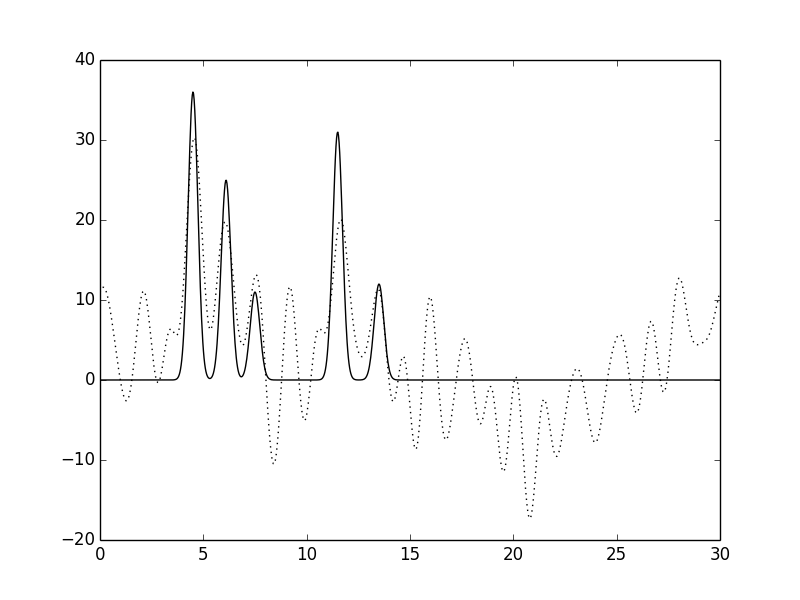
Рис. 15. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением к амплитудам и к фазам 60% шума.
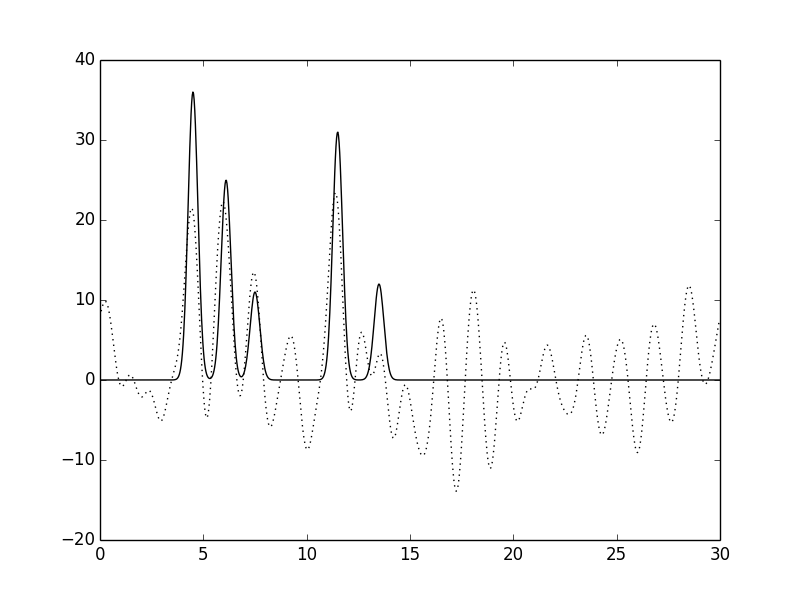
Рис. 16. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением к фазам 20% шума и к амплитудам 60% шума.
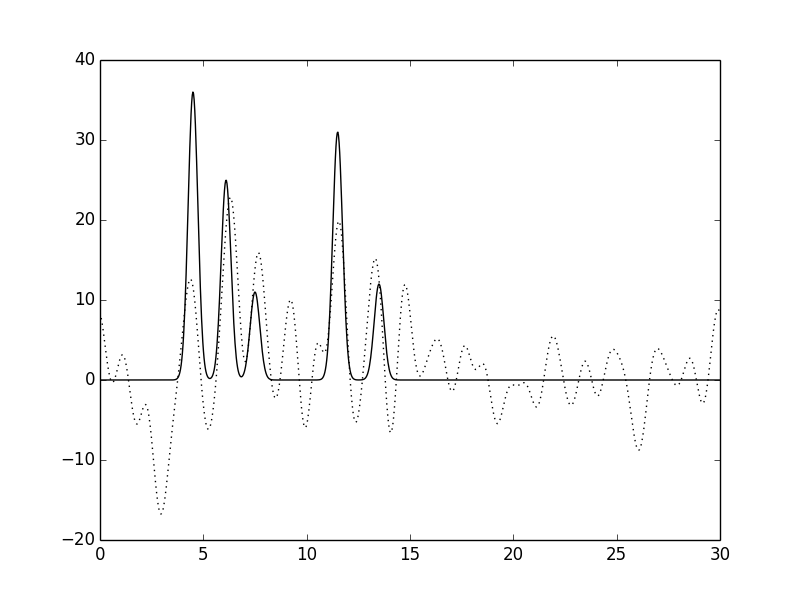
Рис. 17. Функция электронной плотности, восстановленная по первым 30 гармоникам с добавлением к фазам 60% шума и к амплитудам 20% шума.
Можно заметить, что при высокой степени шума как по фазам, так и по амплитудам появляются существенные изменениям вида функции электронной плотности: положения пиков определяются недостаточно точно, а уровень шума на графике увеличивается и его можено принять за дополнительные атомы. Однако увеличение степени шума по фазам влияет на вид функции электронной плотности больше, чем увеличение степени шума по амплитудам.
Восстановление функции электронной плотности по модельным ("экспериментальным") данным с использованием неполного набора гармоникВосстанавливается функция электронной плотности по неполному набору гармоник важно для оценки реального эксперимента, потому что тогда не всегда удается измерить все амплитуды и фазы ряда Фурье. Восстановление функции ЭП по неполным наборам гармоник предсталено на Рис. 18-22.
Например, для восстановления функции электронной плотности на наборе гармоник от 2 до 30 использовались команды:
python fourier-filter.py -r 2-30 -i func_ft.txt -o ft_2-35.txt
python fourier2func.py -i ft_2-30.txt -o two_func_2-30.txt
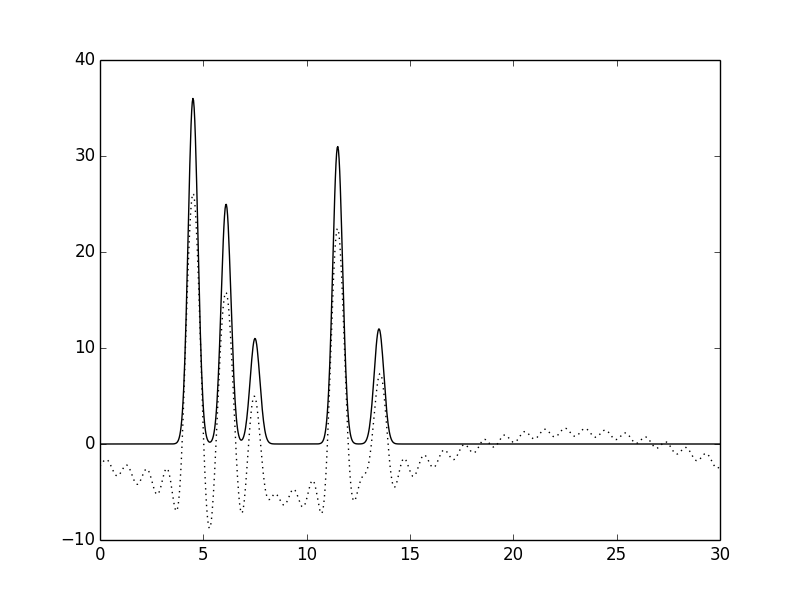
Рис. 18. Функция электронной плотности, восстановленная по наборам гармоник 2-30.
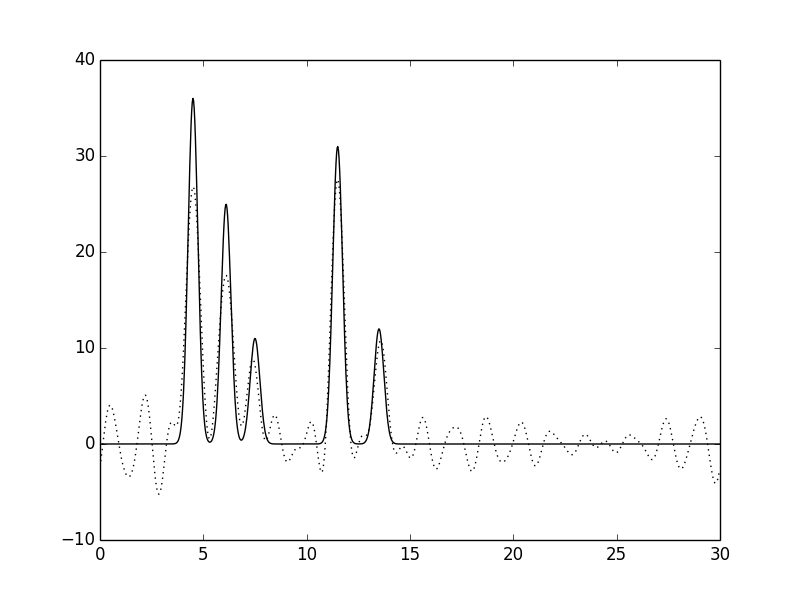
Рис. 19. Функция электронной плотности, восстановленная по наборам гармоник 0-17 и 21-30.
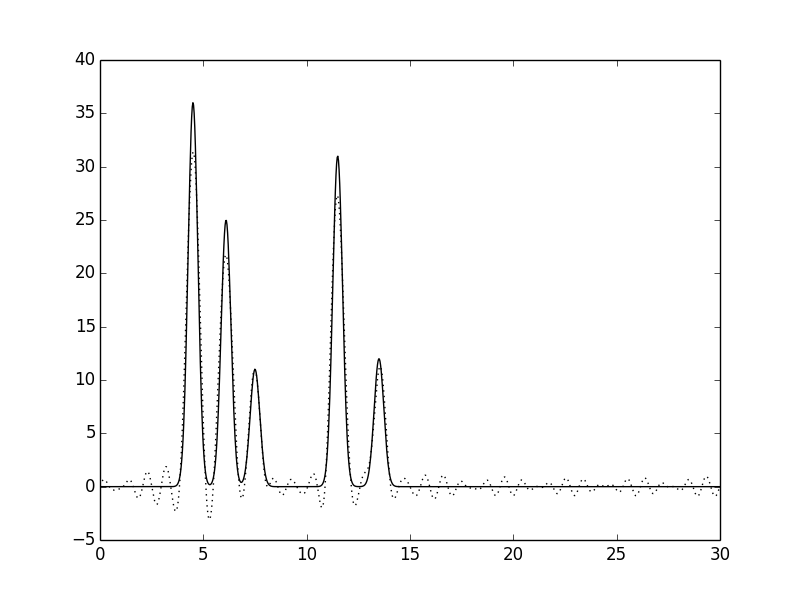
Рис. 20. Функция электронной плотности, восстановленная по наборам гармоник 0-30, 40.
В целом, вид функции мало изменяется при удалении небольшого числа гармоник из любого места: положения пиков определяются достаточно точно, а уровень шума низок и не позволяет определить лишние атомы.
Таблица 1. Восстановление функции электронной плотности в одномерном случае по коэффициентам ряда Фурье.
| Набор гармоник | Разрешение, Å | Полнота данных, % | Шум амплитуды, % от величины F | Шум фазы, % от величины phi | Качество восстановления |
|---|---|---|---|---|---|
| Полный набор гармоник | |||||
| 0-10 | 3 | 100 | 0 | 0 | Плохое |
| 0-20 | 1.5 | 100 | 0 | 0 | Хорошее |
| 0-30 | 1 | 100 | 0 | 0 | Отличное |
| 0-40 | 0.75 | 100 | 0 | 0 | Отличное |
| 0-50 | 0.6 | 100 | 0 | 0 | Отличное |
| 0-30 | 1 | 100 | 0 | 20 | Отличное |
| 0-30 | 1 | 100 | 0 | 40 | Среднее |
| 0-30 | 1 | 100 | 0 | 60 | Плохое |
| 0-30 | 1 | 100 | 20 | 0 | Отличное |
| 0-30 | 1 | 100 | 40 | 0 | Отличное |
| 0-30 | 1 | 100 | 60 | 0 | Хорошее |
| 0-30 | 1 | 100 | 20 | 20 | Отличное |
| 0-30 | 1 | 100 | 40 | 40 | Хорошее |
| 0-30 | 1 | 100 | 60 | 60 | Среднее |
| 0-30 | 1 | 100 | 20 | 60 | Среднее |
| 0-30 | 1 | 100 | 60 | 20 | Хорошее |
| Неполный набор гармоник | |||||
| 2-30 | 1 | 93.3 | 0 | 0 | Отличное |
| 0-17 и 21-30 | 1 | 0.9 | 0 | 0 | Отличное |
| 0-30 и 40 | 1 | 0.75 | 0 | 0 | Отличное |
Разрешением полного набора гармоник называется период гармоники с номером n, т.е. с наибольшим номером. Период гармоники равен расстоянию между соседними максимумами синусоиды; его также называют длиной волны этой гармоники. Для полного набора данных (разрешение d=T/n) полнота равна 100%.
Для неполного набора данных нет строгого определения разрешения. Кроме разрешения d необходимо сообщить полноту данных — процент определенных гармоник с длиной волны больше d от максимально возможного количества гармоник. Разрешение неполного набора гармоник было определено для порогового значения полноты набора 90% - за разрешение было принято такое число d, что при полноте наборе данных 90%, d - разрешение минимальной гармоники.