Восстановление кристалла из PDB файла

В данном практикуме необходило было изучить кристаллическую ячейку белка. Из содержимого поля CRYST1 из pdb получаем характеристики векторов кристалла - таблица 1.

Таблица 1. Параметры векторов кристалла

Вектор	Длина	Угол (в градусах)
a	185.050 A	90.00
b	106.800 A	112.00
c	152.700 A	190.00

Кристаллографическая группа кристалла H3 (сейчас в номенклатуре чаще используется эквивалентная формула – P3 (H3 – гексагональная нотация (рис.1), P3 – для примитивной элементарной ячейки ( рис.2)). Число молекул в одной ячейке равно 9. 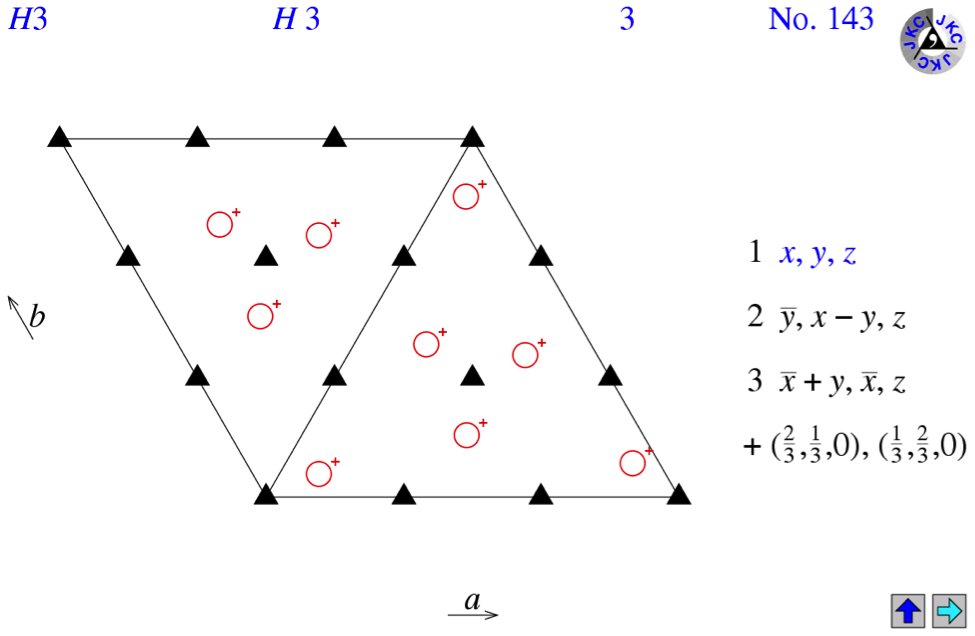Рисунок 1. H3 группа симметрии

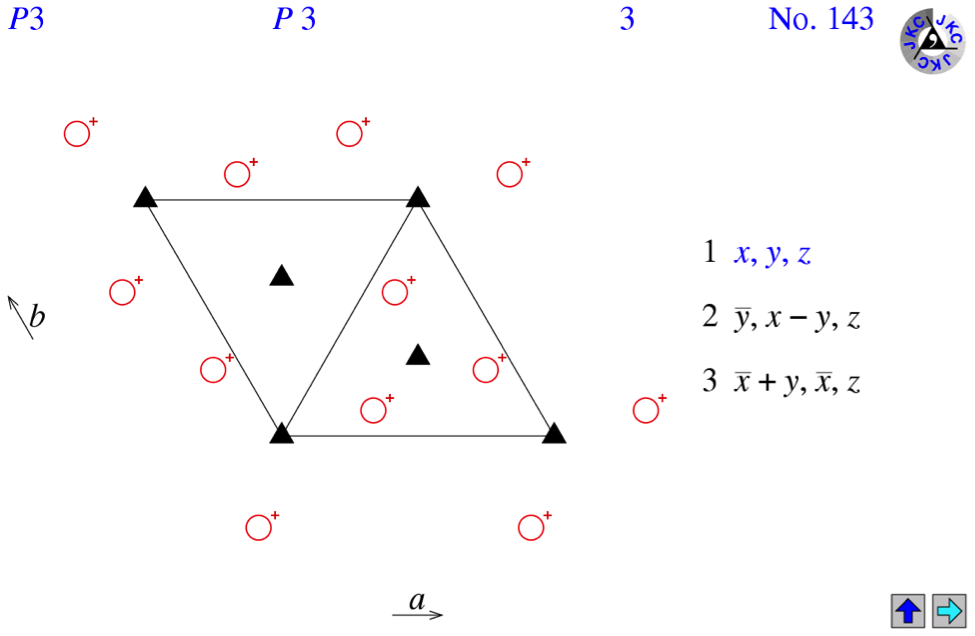Рисунок 2. P3 группа симметрии

Для построения соседних молекул кристалла используем комманду

symexp 4guw, 4guw, 5

Получаем соседние ячейки - рис. 3.. Даже не первый взгляд области контакта между ячейками малы (рис. 4.), pymol находит едичные водородные связи в областях этих контактов (рис. 5.). Таким образом эти взаимодействия с большой вероятностью обусловлены просто плотной упаковкой молекул в кристалле.

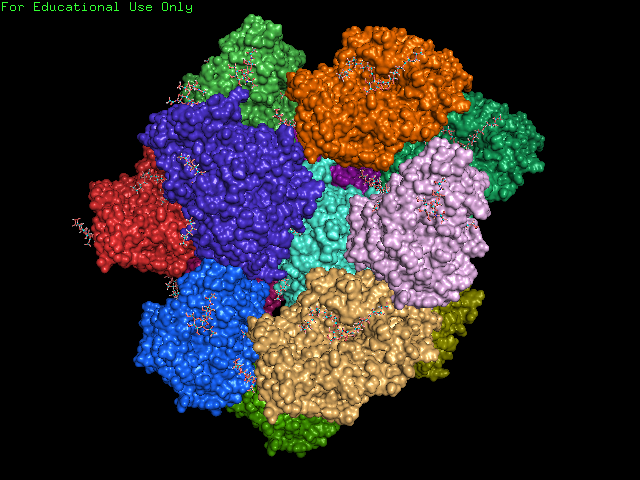
Рисунок 3. Визуализация соседних ячеек, исходная структура показана голубым цветом.

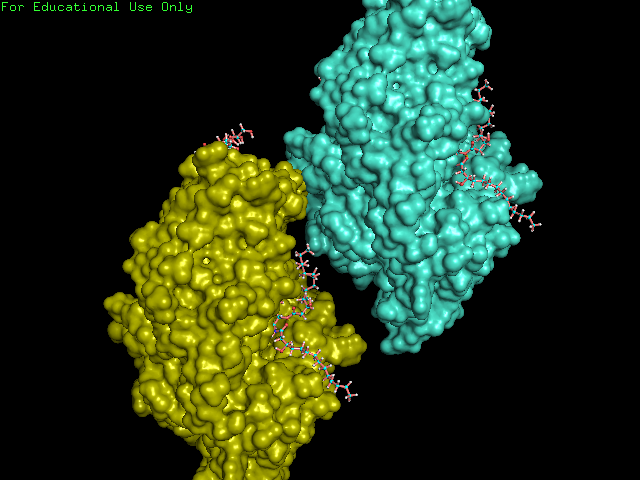Рисунок 4. Область контакта между двумя молекулами крайне мала.

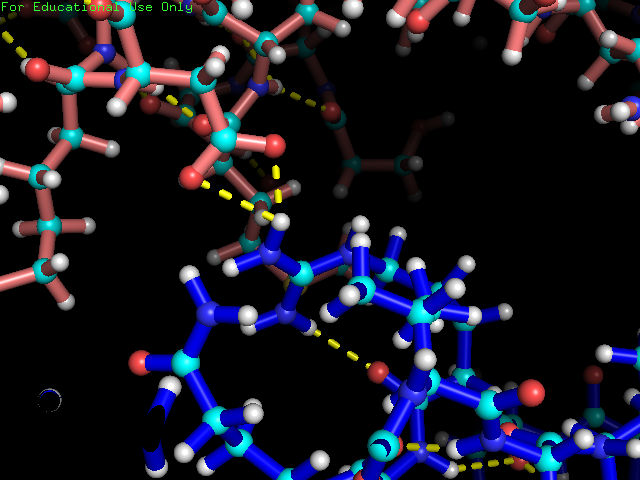Рисунок 5. Цепь одной молекулы покрашена в красный, второй - в синий. Единичная водородная связь вряд ли способна удержать молекулы белка в растворе рядом.

Для следующей части практикума мною была выбрана структура 3DTT комплекса белка с ДНК, где белок находится «на краю» ДНК, что подозрительно (рис. 6.) При построении симметричной ячейки видим, что две молекулы ДНК «цепляются друг за друга» за липкие концы и наш белок сидит именно на месте их контакта.(рис. 7.)

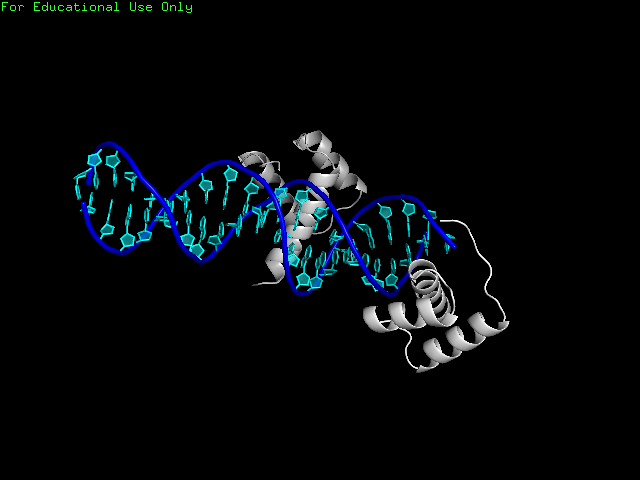
Рисунок 6. Визуализация комплексе белка с ДНК, аномальная единица белка расположена на "краю" ДНК.

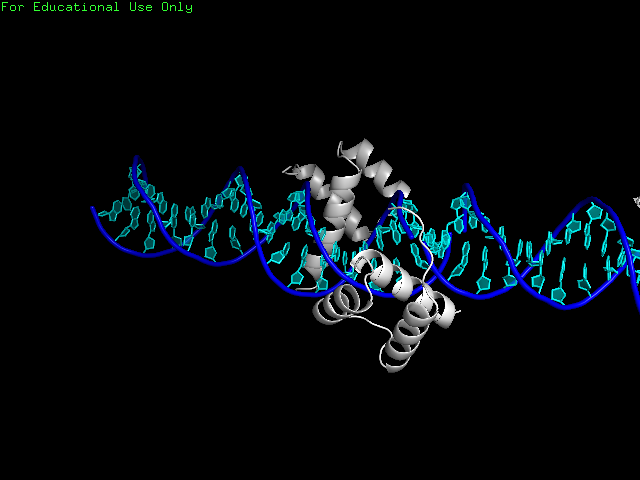
Рисунок 7. При построении симметричной ячейки видим, что на самом деле она сидит на стыке двух молекул ДНК.

Следующим заданием практикума было найти примеры PDB-файлов, в которых ассиметричная единица не совпадает с биологической единицей. С помошью Advanced search PDB мною были найдены два примера. Первый пример - структура 5B6V, у которой биологическая единица состоит из ассиметрических формирующих вместе комплекс - рис. 8. и рис. 9.

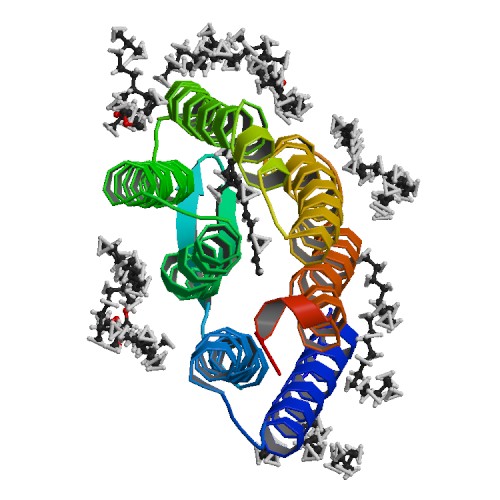
Рисунок 8. Ассиметрическая единица белка 5B6V.

Рисунок 9. Биологическая единица белка 5B6V.

Следующий пример - структура 5THS. У нее в отличие от предыдущего, ассиметричная единица больше биологической и состоит из двух биологических (рис. 10 и рис. 11). Для того, чтобы такое получилось необходимо, чтобы биологические единицы в составе ассиметричной заметно отличались по своим конформациям. Однако также это используют (необоснованно, конечно) для того, чтобы увеличить число параметров подгонки при оптимизации и получить лучший R-factor. Беглый взгляд на две субъединицы и их выравнивание с очень низким RSMD говорит, к сожалению, именно в пользу второго варианта.

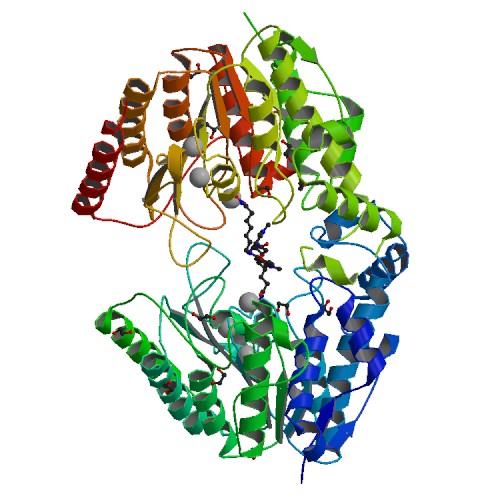
Рисунок 10. Ассиметричная единица белка 5THS

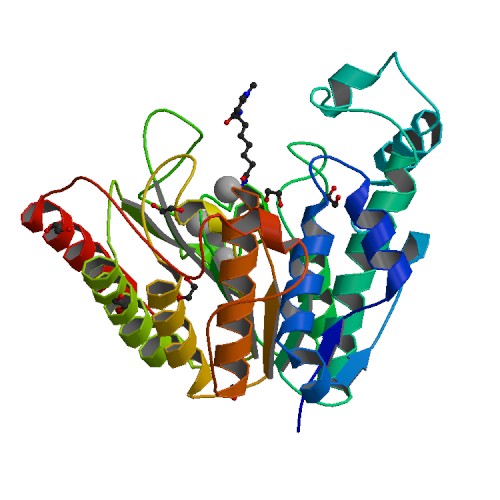
Рисунок 11. Биологическая единица белка 5THS