Восстановление электронной плотности

Eritis sicut Deus, scientes bonum et malum

Сайт студента ФББ Пензара Дмитрия

Отчет по качеству РСА расшифровки структуры Построение поверхности Совмещение структур Определение вторичной структуры Файл результатов РСА экспериментов Использование сервисов PDB Интерпретация ЯМР структуры Нахождение гидрофобных кластеров Восстановление электронной плотности Построение и визуализация электронной плотности Восстановление кристалла из PDB файла Сравнение доменов SCOP/SCOPe, ECOD, CATH и Pfam

Описание используемой модели

На одномерном отрезке длино1 30 ангстрем и началом в 0 расположены две молекулы, состояющие из трех атомов. Атомы в каждой молекуле связыны ковалентно и находятся на расстоянии 1-1.5 Ангестрема. Молекулы расположены на расстоянии 4-5А (водородная связь или гидрофобное взаимодействие). Электронные плотности атомов описываются гауссовой кривой. Функция электронной плотности на отрезке была задана при помощи скрипта compile_func.py, вызванного командой

python compile_func.py -g 5,2,2+28,3,3+5,2,4+32,2,7.4+64,2.5,8.8+32,2,10.2

В результате была получена электронная плотность вида - рис.1 Полученная функция была разложена в ряд Фурье с помощью скрипта func2fourier.py с помощью команды

python func2fourier.py -i func.txt

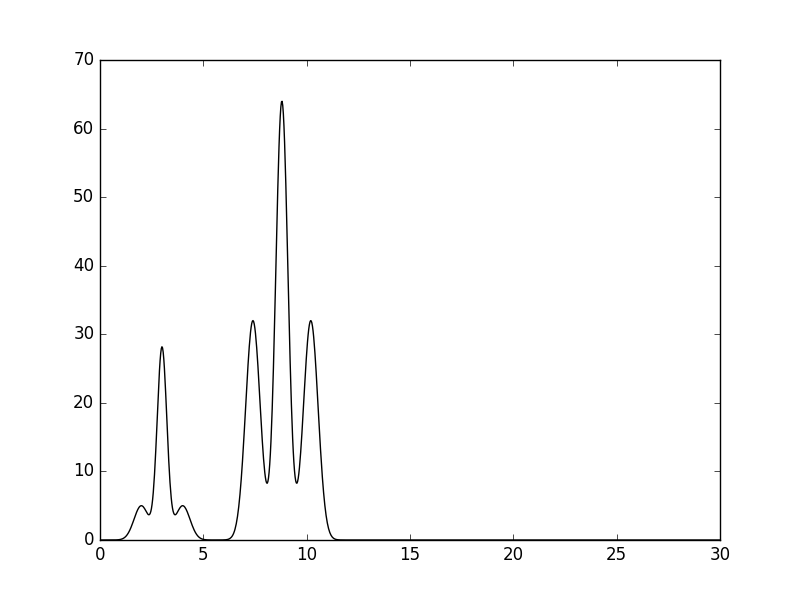
Электронная плотность исследуемой модели

Использовались следующие критерии качества: Отличное восстановление – по графику восстановленной функции можно определить положение максимума всех гауссовых слагаемых функции ("атомов") Хорошее восстановление – можно угадать положение всех максимумов, зная число слагаемых ("атомов"), хотя на восстановленной функции максимумы от атомов не отличимы от шума Среднее восстановление – положение каких-то атомов определить по восстановленной функции нельзя, других - можно Плохое восстановление – положение атомов определить не представляется возможным; можно только предсказать примерный размер "молекулы"

Скриптом было сгенерирована 499 гармоника, что явно исбыточно. Потому вначале был определен оптимальный набор гармоник 0..n0, для которых функции восстанавливается отлично (таблица 1). Было выбрано число n0 = 33.

Таблица. 1. Подбор n0.

n0	Разрешение	Качество
499	0.06	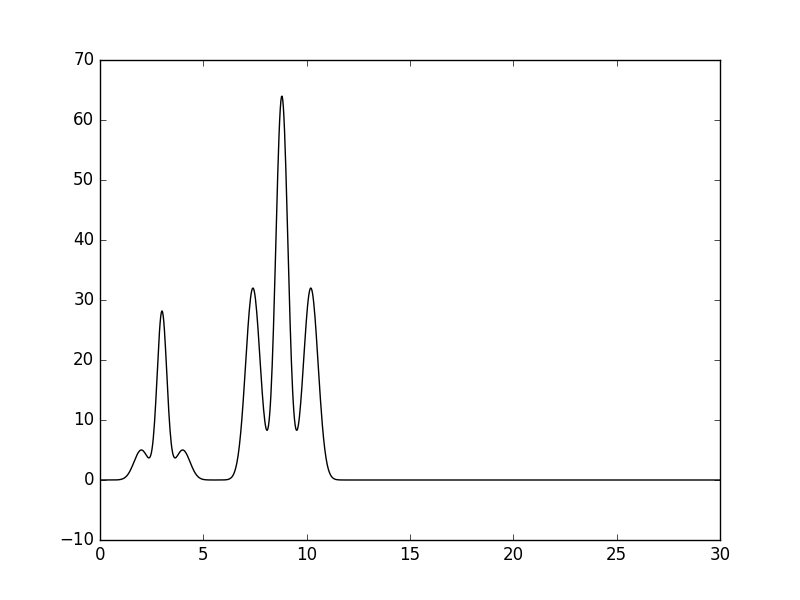Отличное
1	15	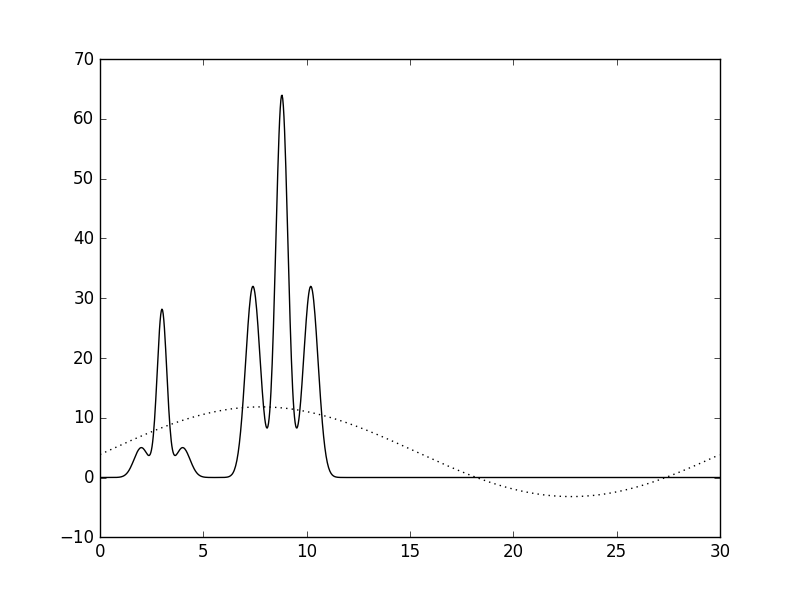Невозможно восстановить
10	2.72	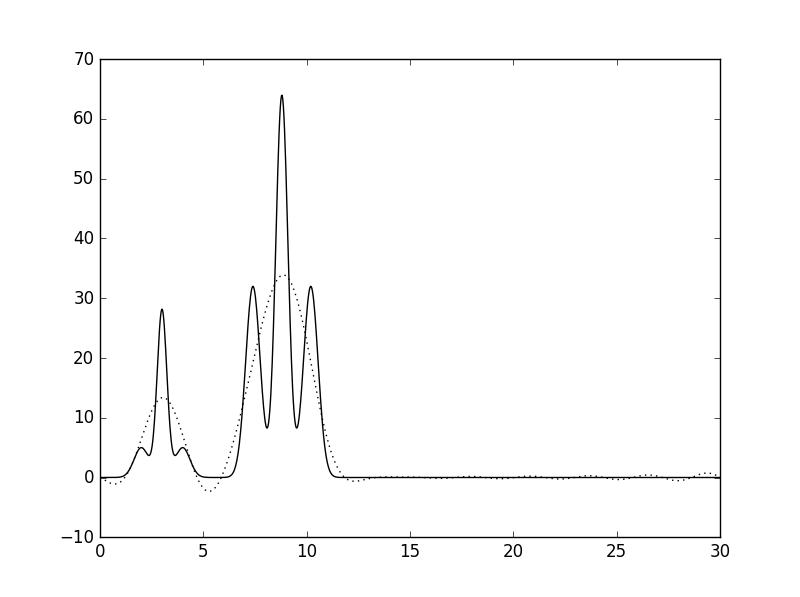Плохое
20	1.43	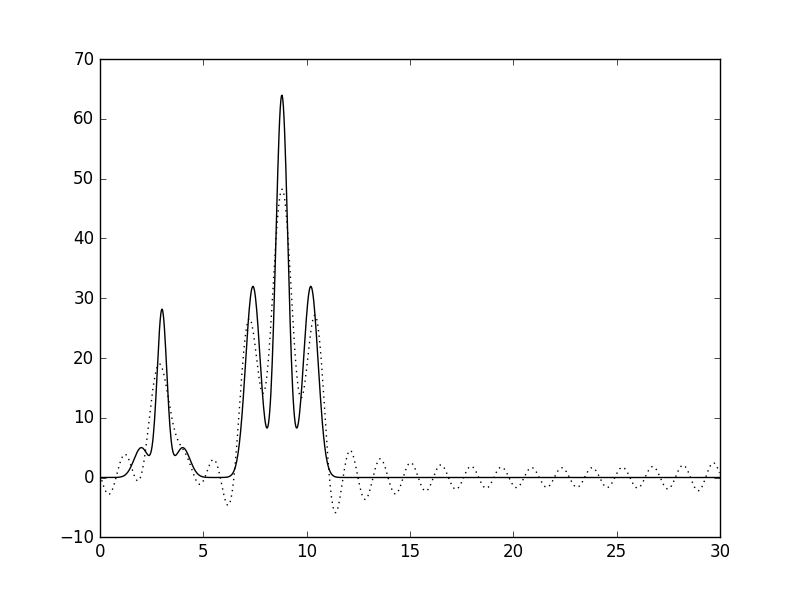Хорошее
30	0.97	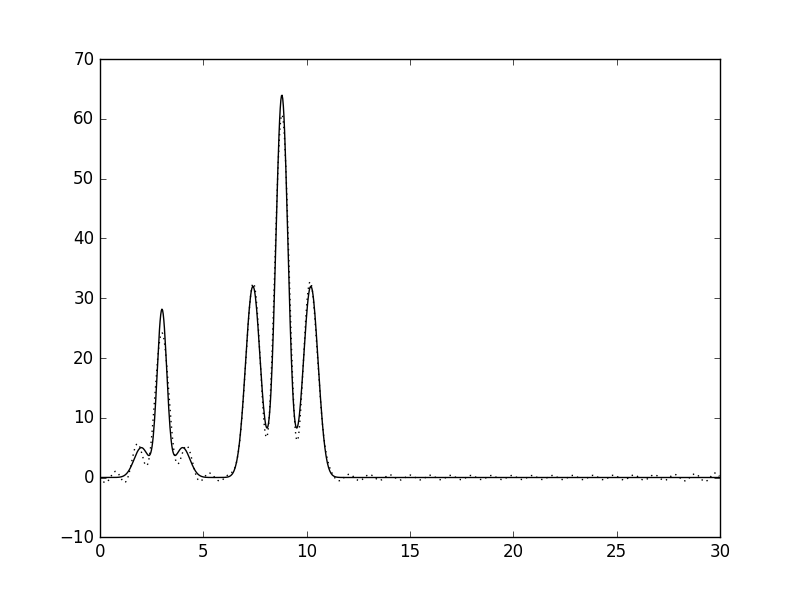Отличное
35	0.83	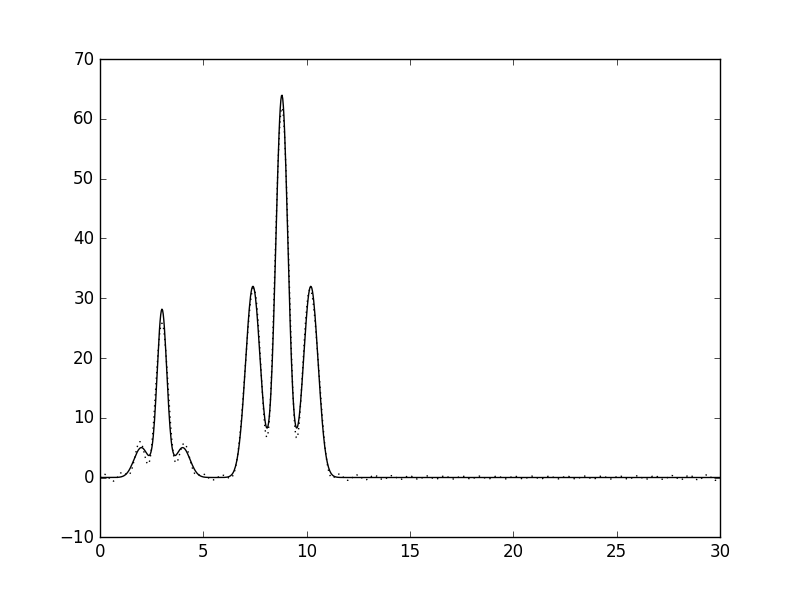Отличное
33	0.88	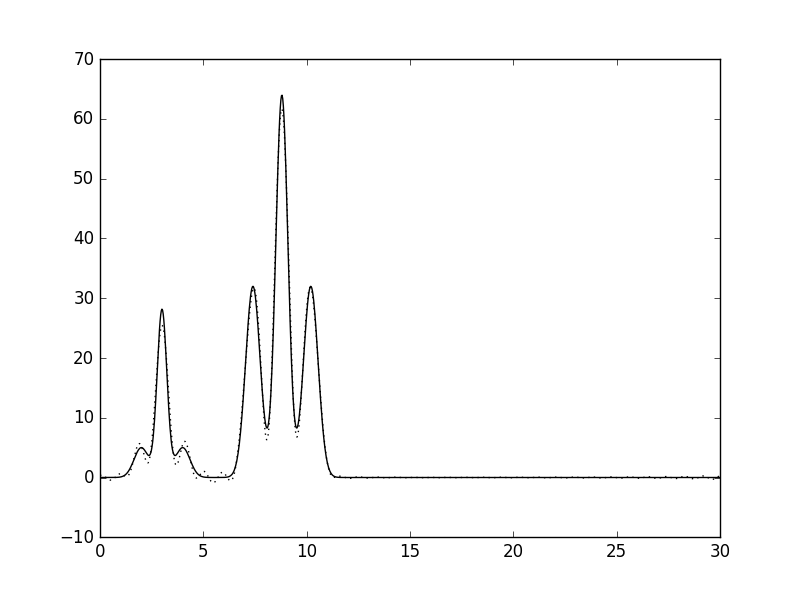Отличное

Дальнейшей целью было изучение влияния шума на качество восстановления. Шум можно было добавлять к фазе (в процентах - обозначалось P) и к амплитуде (в процентах - F) разложения фурье. Из таблицы 2 видно, что добавление шума к фазе сильнее влияет на качество восстановления, чем добавление шума к амплитуде.

Таблица. 2. Влияние шума на качество восстановления. Каждый раз использовался набор гармоник 0-33

F (% шума к амплитуде)	P (% шума к фазе)	Качество
10	0	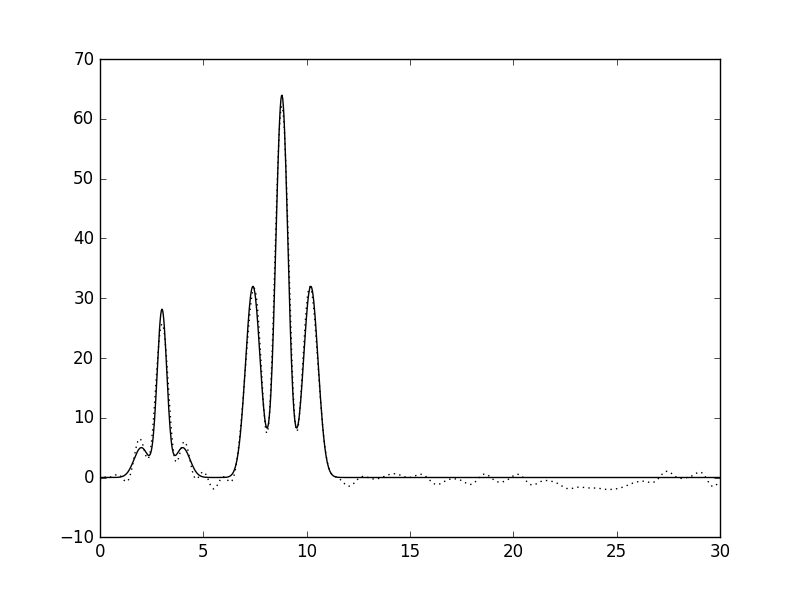Отличное
15	0	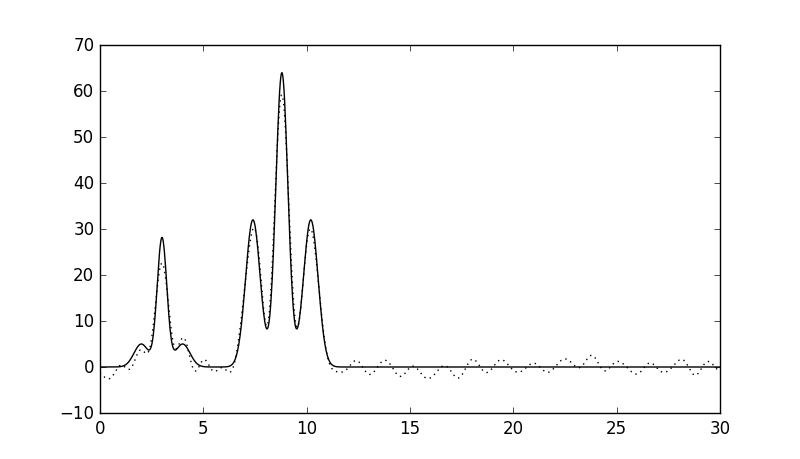Хорошее
20	0	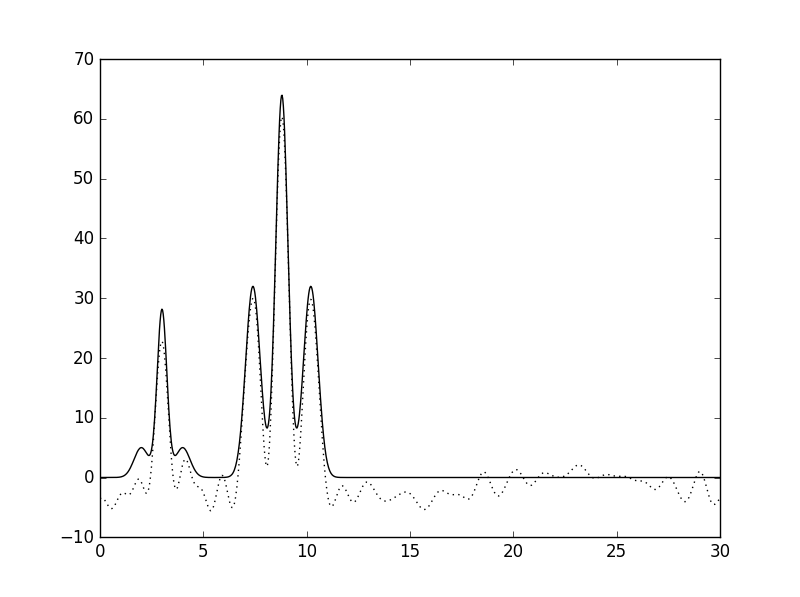Среднее
50	0	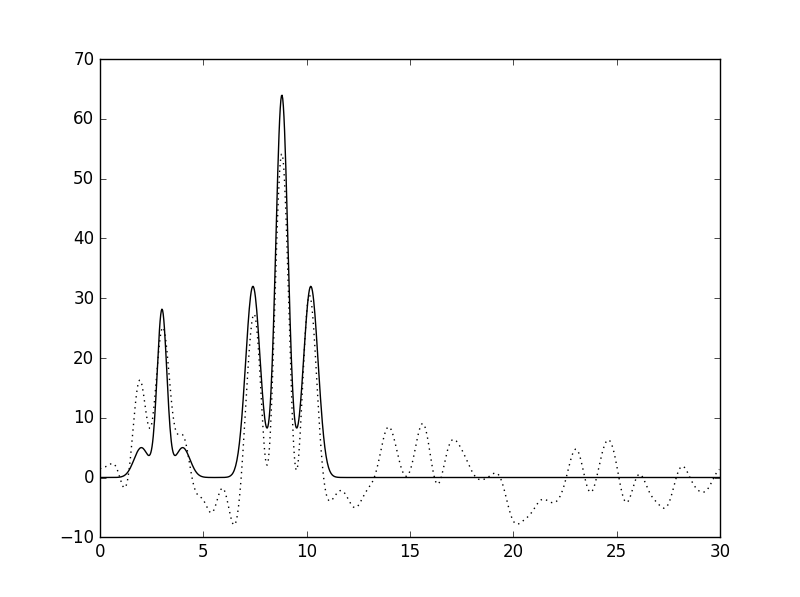Среднее
0	10	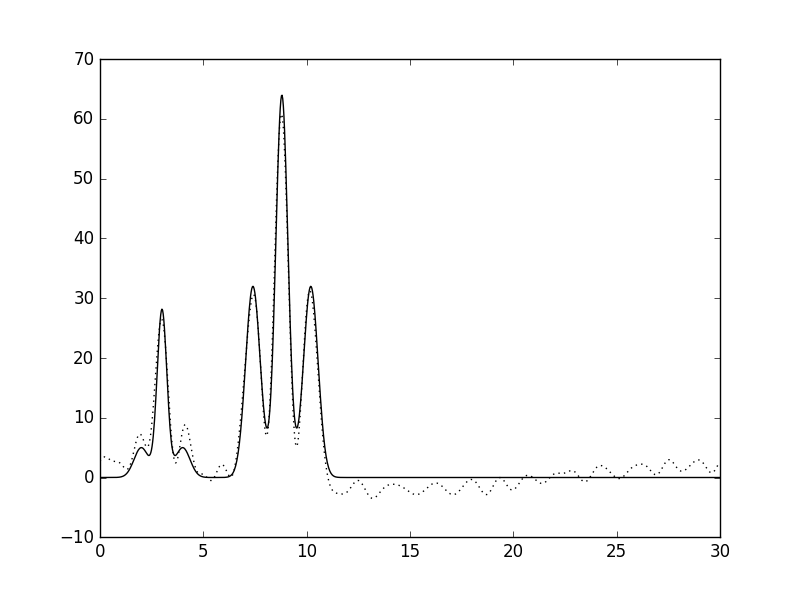Среднее
0	15	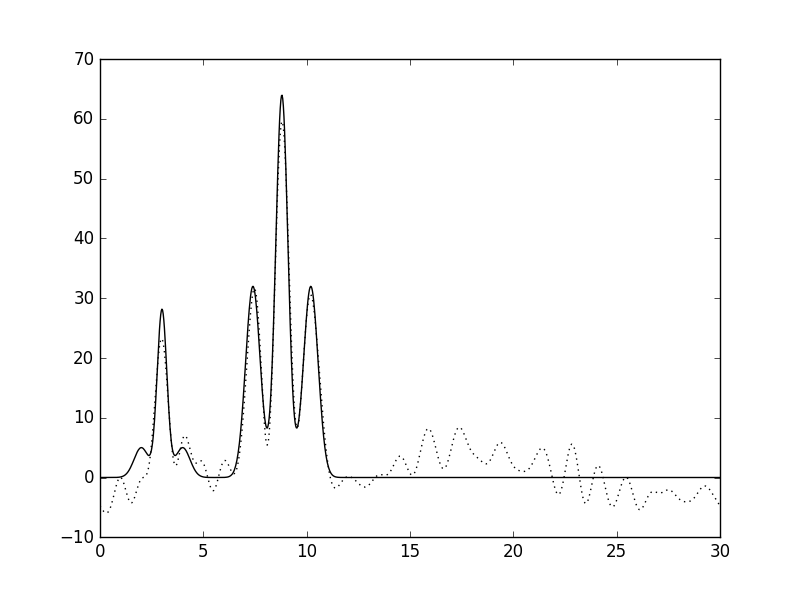Среднее
0	20	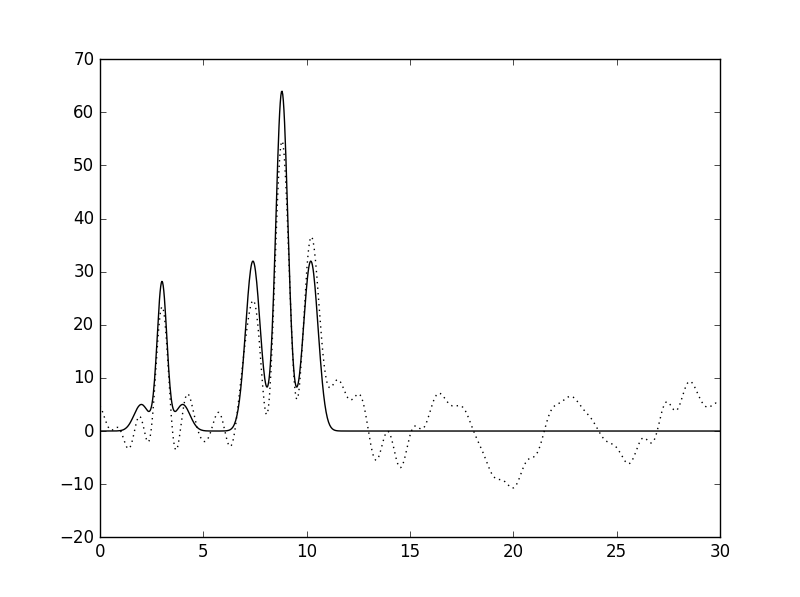Среднее
0	50	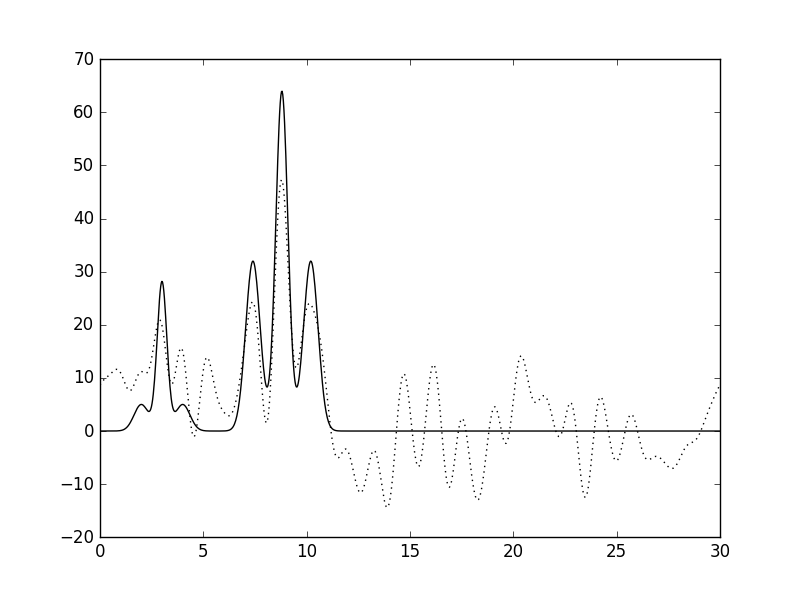Плохое
10	10	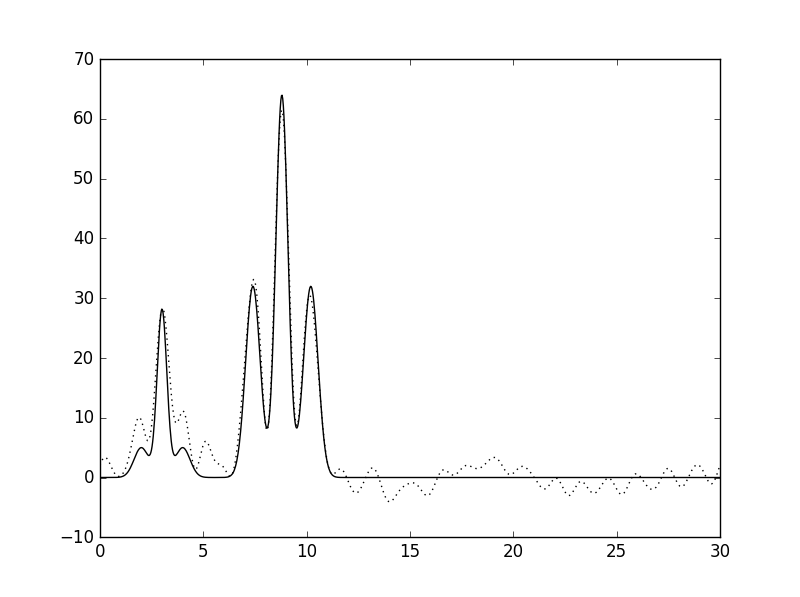Отличное
15	15	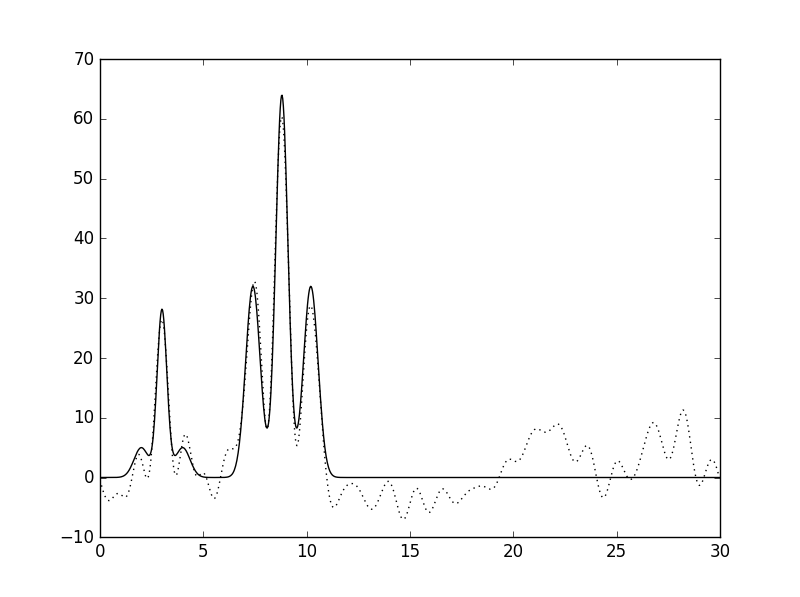Среднее
20	20	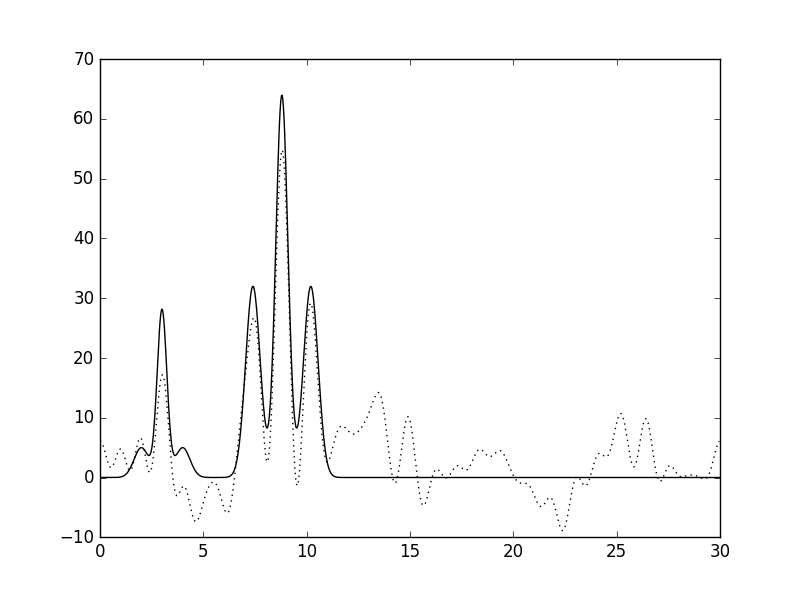Среднее
50	50	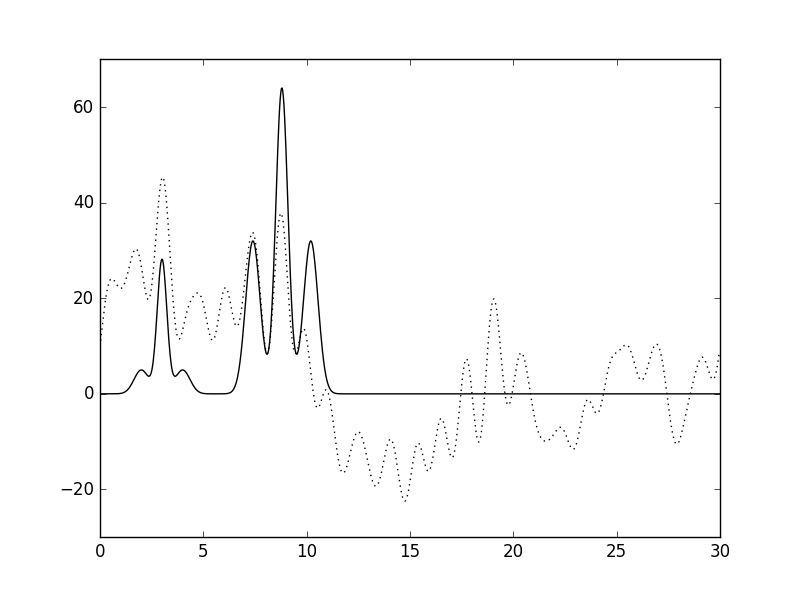Плохое

Теперь изучим качество восстановления при неполном наборе гармоник. Из таблицы 3 видно, что наиболее важными являются гармоники из середины набора, т.к выбрасывание первых гармоник и добавление последних не сильно изменяли качество восстановления.

Таблица. 3. Влияние полноты набора гармоник на качество восстановления.

Набор гармоник	Разрешение	Полнота набора	Качество
1-33	0.88	0.97	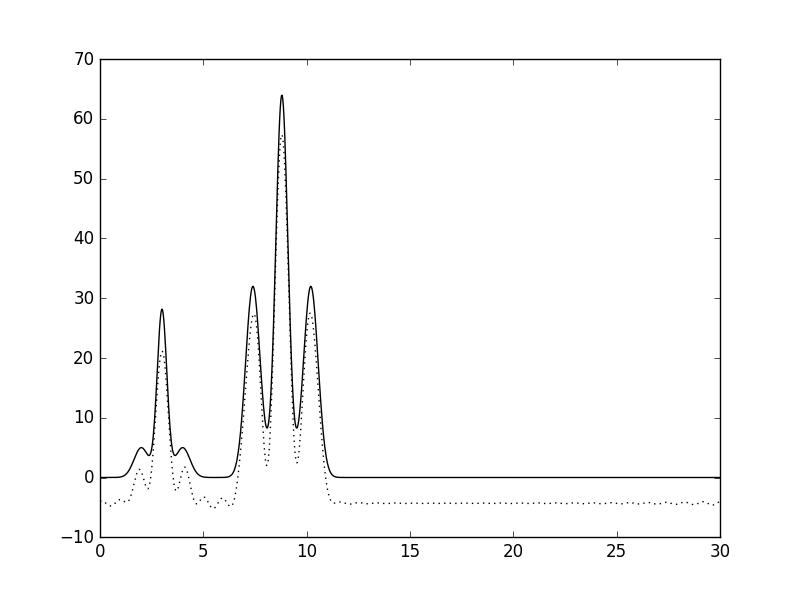Отличное
2-33	0.88	0.94	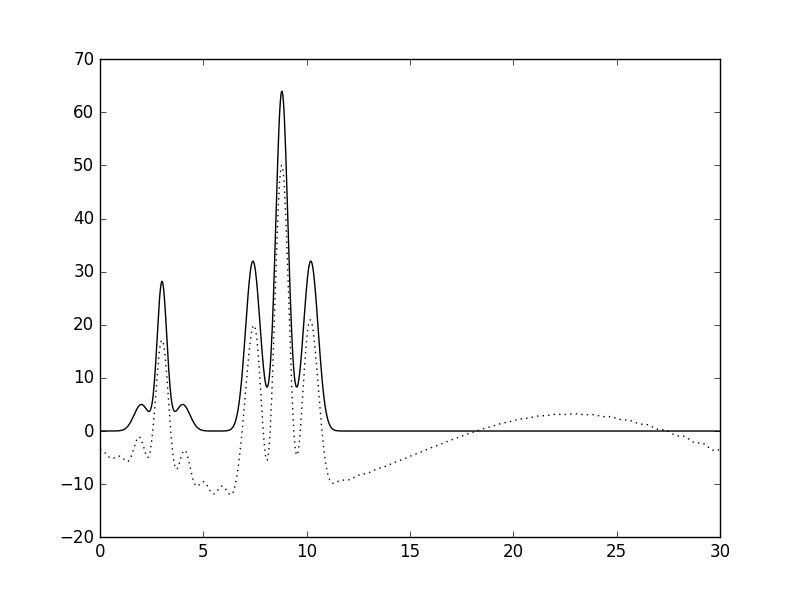Отличное
2-15, 20-33	0.88	0.82	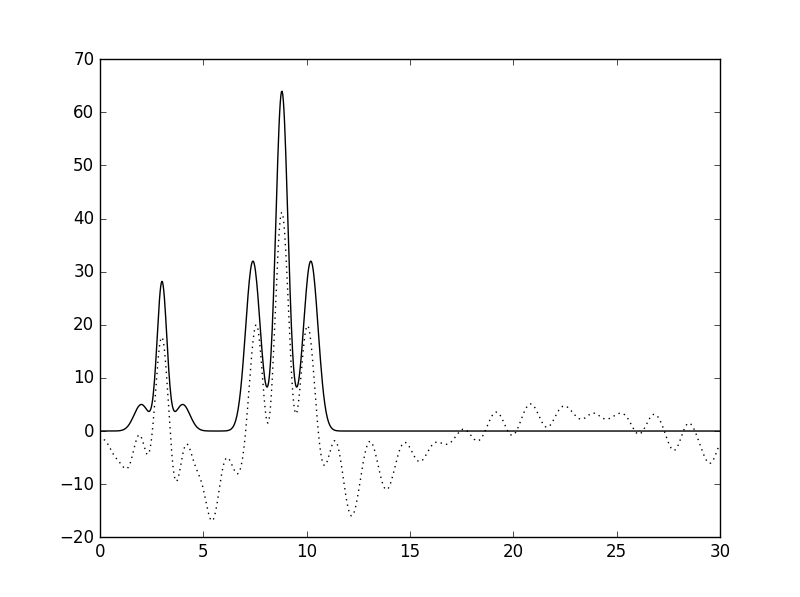Хорошее
2-15, 20-33, 40	0.88	0.97	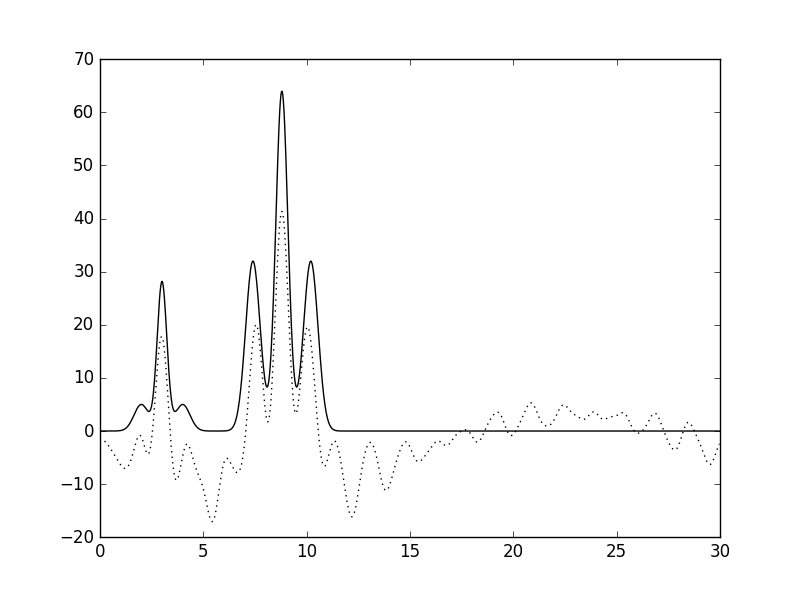Хорошее

Несмотря на это можно заключить, что качество структуры достаточно высокое (требование к определению положения боковой цепи на большом уровне подрезки достаточно избыточно, да и понятно, что боковые цепи детектировать значительно сложнее). Потому структура прекрасно подходит для дальнейшей работы.